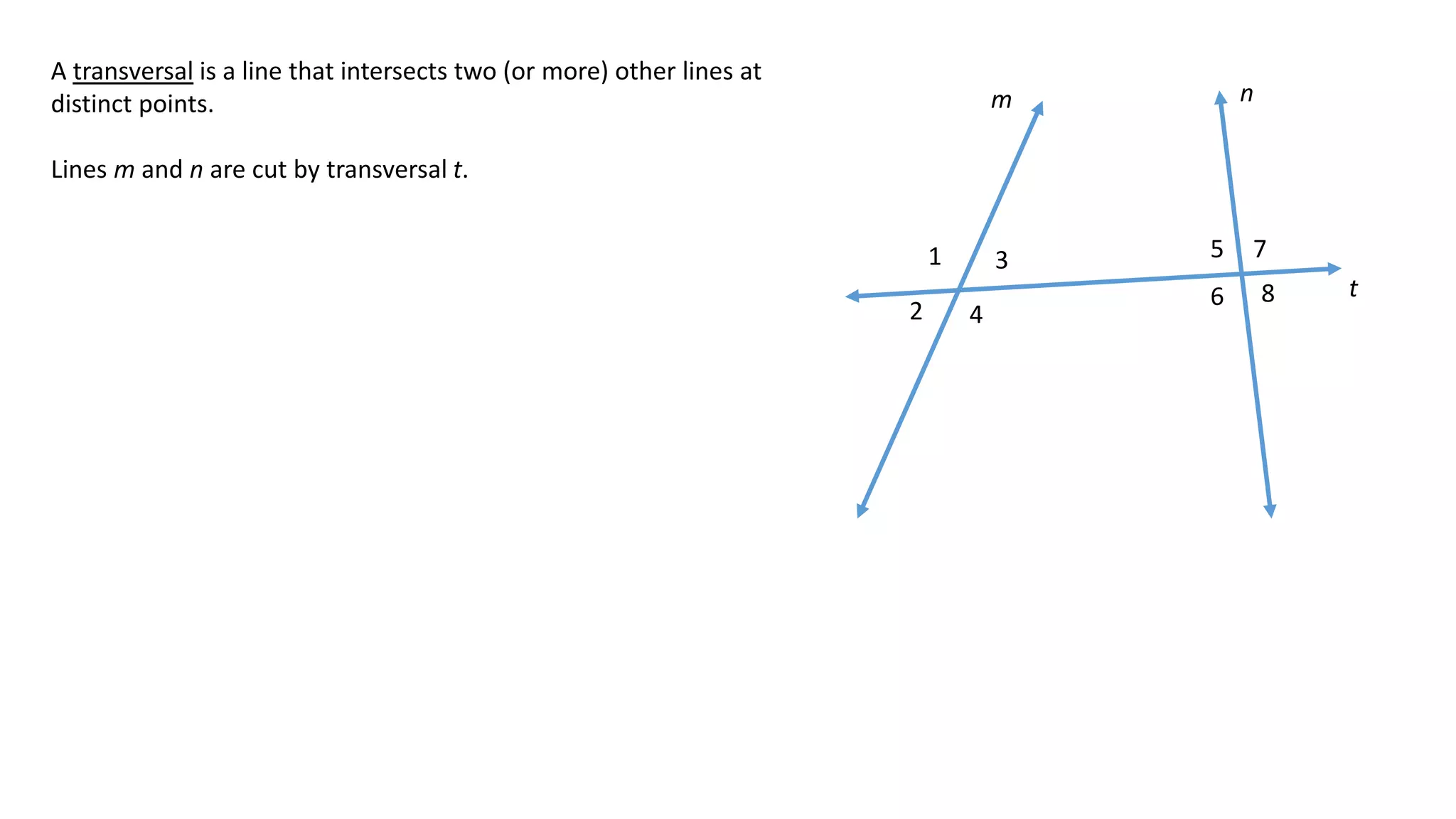
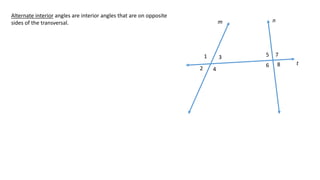
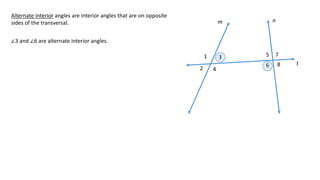
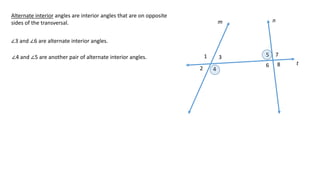
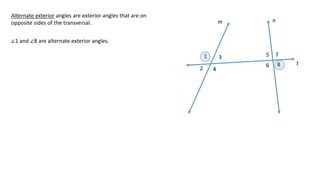
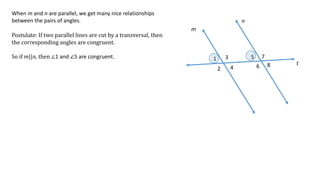
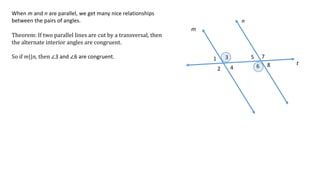
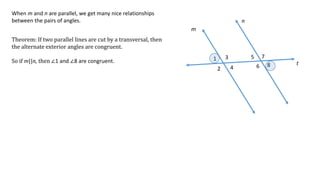
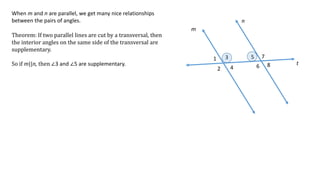
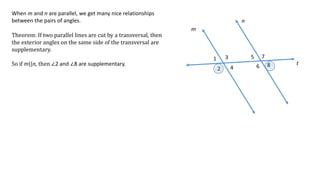
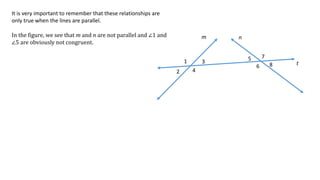
The document defines and describes different types of angles formed when two lines are cut by a transversal line, including interior angles, exterior angles, corresponding angles, alternate interior angles, and alternate exterior angles. It also explains properties and relationships between these angles, such as corresponding angles being congruent and alternate angles being congruent, that hold true when the two lines are parallel but not necessarily when the lines are not parallel.

1. 1
2
3
4
5
6
7
8
m n
t
A transversal is a line that intersects two (or more) other lines at
distinct points.
Lines m and n are cut by transversal t.

2. 1
2
3
4
5
6
7
8
m n
t
Interior angles are angles that are between the lines.

3. 1
2
3
4
5
6
7
8
m n
t
Interior angles are angles that are between the lines.
∠3, ∠4, ∠5, and ∠6 are interior angles.

4. 1
2
3
4
5
6
7
8
m n
t
Interior angles are angles that are between the lines.
∠3, ∠4, ∠5, and ∠6 are interior angles.
Exterior angles are angles that are between the lines.

5. 1
2
3
4
5
6
7
8
m n
t
Interior angles are angles that are between the lines.
∠3, ∠4, ∠5, and ∠6 are interior angles.
Exterior angles are angles that are between the lines.
∠1, ∠2, ∠7, and ∠8 are exterior angles.

6. 1
2
3
4
5
6
7
8
m n
t
Corresponding angles are angles that are in the same relative
positions when compared to the points of intersection.

7. 1
2
3
4
5
6
7
8
m n
t
Corresponding angles are angles that are in the same relative
positions when compared to the points of intersection.
∠1 and ∠5 are a pair of corresponding angles because they are
both up and to the left of the points of intersection.

8. 1
2
3
4
5
6
7
8
m n
t
Corresponding angles are angles that are in the same relative
positions when compared to the points of intersection.
∠1 and ∠5 are a pair of corresponding angles because they are
both up and to the left of the points of intersection.

9. 1
2
3
4
5
6
7
8
m n
t
Corresponding angles are angles that are in the same relative
positions when compared to the points of intersection.
∠1 and ∠5 are a pair of corresponding angles because they are
both up and to the left of the points of intersection.
∠3 and ∠7 are a pair of corresponding angles because they are
both up and to the right of the points of intersection.

10. 1
2
3
4
5
6
7
8
m n
t
Corresponding angles are angles that are in the same relative
positions when compared to the points of intersection.
∠1 and ∠5 are a pair of corresponding angles because they are
both up and to the left of the points of intersection.
∠3 and ∠7 are a pair of corresponding angles because they are
both up and to the right of the points of intersection.
∠2 and ∠6 are a pair of corresponding angles because they are
both down and to the left of the points of intersection.

11. 1
2
3
4
5
6
7
8
m n
t
Corresponding angles are angles that are in the same relative
positions when compared to the points of intersection.
∠1 and ∠5 are a pair of corresponding angles because they are
both up and to the left of the points of intersection.
∠3 and ∠7 are a pair of corresponding angles because they are
both up and to the right of the points of intersection.
∠2 and ∠6 are a pair of corresponding angles because they are
both down and to the left of the points of intersection.
∠4 and ∠8 are a pair of corresponding angles because they are
both down and to the right of the points of intersection.

12. 1
2
3
4
5
6
7
8
m n
t
Alternate interior angles are interior angles that are on opposite
sides of the transversal.

13. 1
2
3
4
5
6
7
8
m n
t
Alternate interior angles are interior angles that are on opposite
sides of the transversal.
∠3 and ∠6 are alternate interior angles.

14. 1
2
3
4
5
6
7
8
m n
t
Alternate interior angles are interior angles that are on opposite
sides of the transversal.
∠3 and ∠6 are alternate interior angles.
∠4 and ∠5 are another pair of alternate interior angles.

15. 1
2
3
4
5
6
7
8
m n
t
Alternate exterior angles are exterior angles that are on
opposite sides of the transversal.

16. 1
2
3
4
5
6
7
8
m n
t
Alternate exterior angles are exterior angles that are on
opposite sides of the transversal.
∠1 and ∠8 are alternate exterior angles.

17. 1
2
3
4
5
6
7
8
m n
t
Alternate exterior angles are exterior angles that are on
opposite sides of the transversal.
∠1 and ∠8 are alternate exterior angles.
∠2 and ∠7 are another pair of alternate exterior angles.

18. m
n
Parallel lines are lines that will never intersect, no matter how
far we extend them.
We can write m||n.

19. 1
2
3
4
5
6
7
8
m
n
t
When m and n are parallel, we get many nice relationships
between the pairs of angles.

20. 1
2
3
4
5
6
7
8
m
n
t
When m and n are parallel, we get many nice relationships
between the pairs of angles.
Postulate: If two parallel lines are cut by a transversal, then
the corresponding angles are congruent.
So if m||n, then ∠1 and ∠5 are congruent.

21. 1
2
3
4
5
6
7
8
m
n
t
When m and n are parallel, we get many nice relationships
between the pairs of angles.
Theorem: If two parallel lines are cut by a transversal, then
the alternate interior angles are congruent.
So if m||n, then ∠3 and ∠6 are congruent.

22. 1
2
3
4
5
6
7
8
m
n
t
When m and n are parallel, we get many nice relationships
between the pairs of angles.
Theorem: If two parallel lines are cut by a transversal, then
the alternate exterior angles are congruent.
So if m||n, then ∠1 and ∠8 are congruent.

23. 1
2
3
4
5
6
7
8
m
n
t
When m and n are parallel, we get many nice relationships
between the pairs of angles.
Theorem: If two parallel lines are cut by a transversal, then
the interior angles on the same side of the transversal are
supplementary.
So if m||n, then ∠3 and ∠5 are supplementary.

24. 1
2
3
4
5
6
7
8
m
n
t
When m and n are parallel, we get many nice relationships
between the pairs of angles.
Theorem: If two parallel lines are cut by a transversal, then
the exterior angles on the same side of the transversal are
supplementary.
So if m||n, then ∠2 and ∠8 are supplementary.

25. 1
2
3
4
5
6
7
8
m n
t
It is very important to remember that these relationships are
only true when the lines are parallel.
In the figure, we see that m and n are not parallel and ∠1 and
∠5 are obviously not congruent.