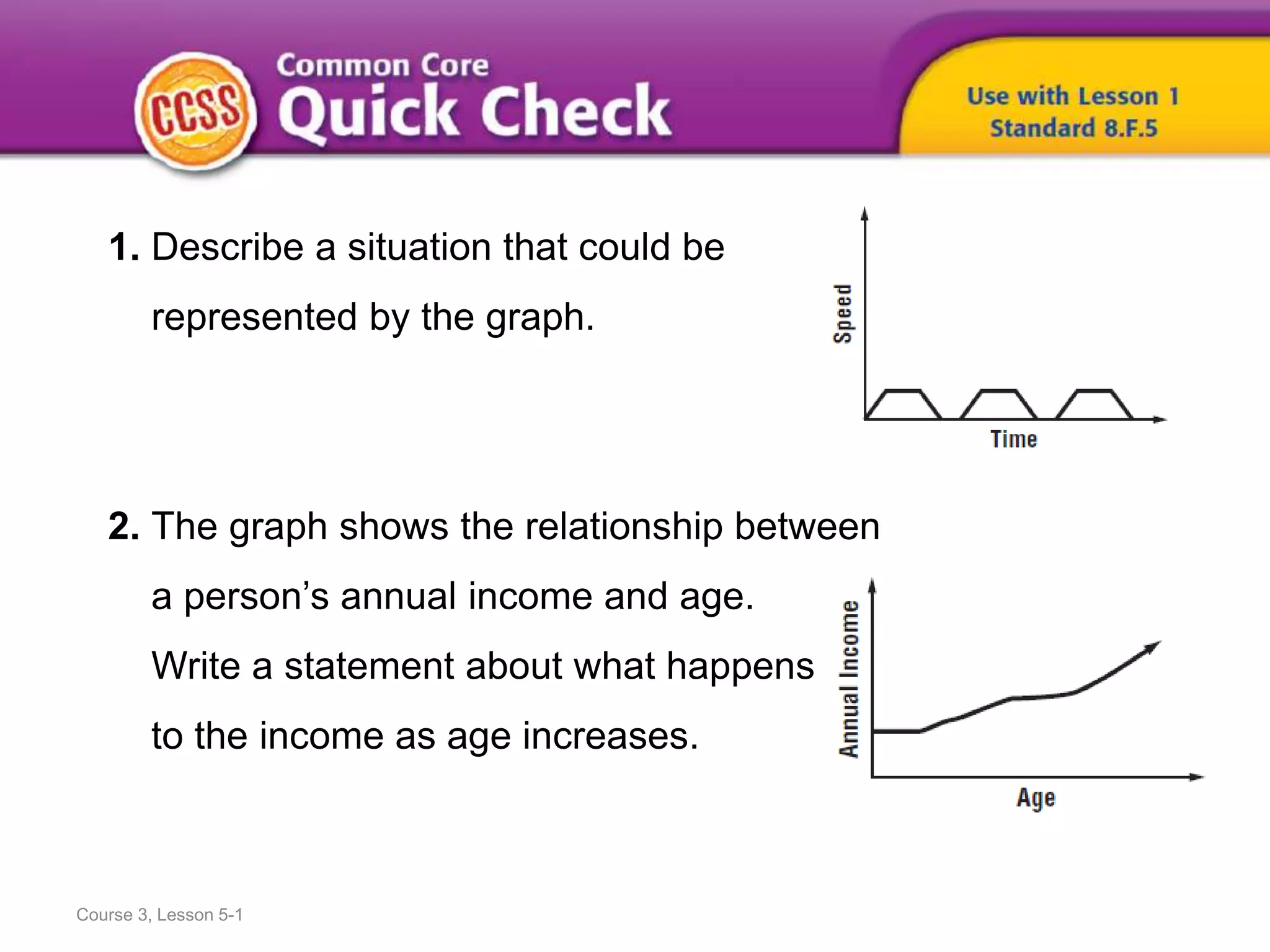
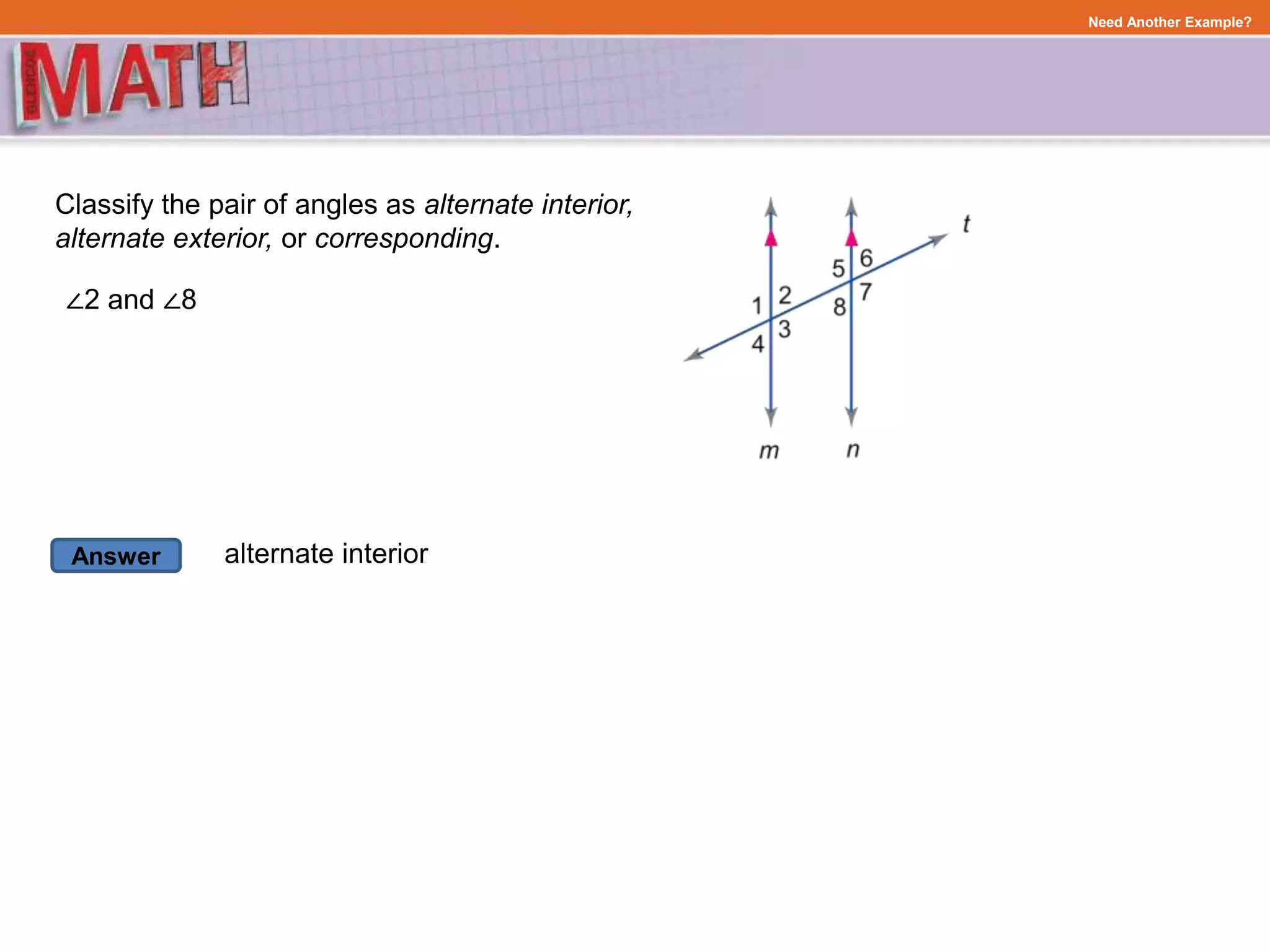
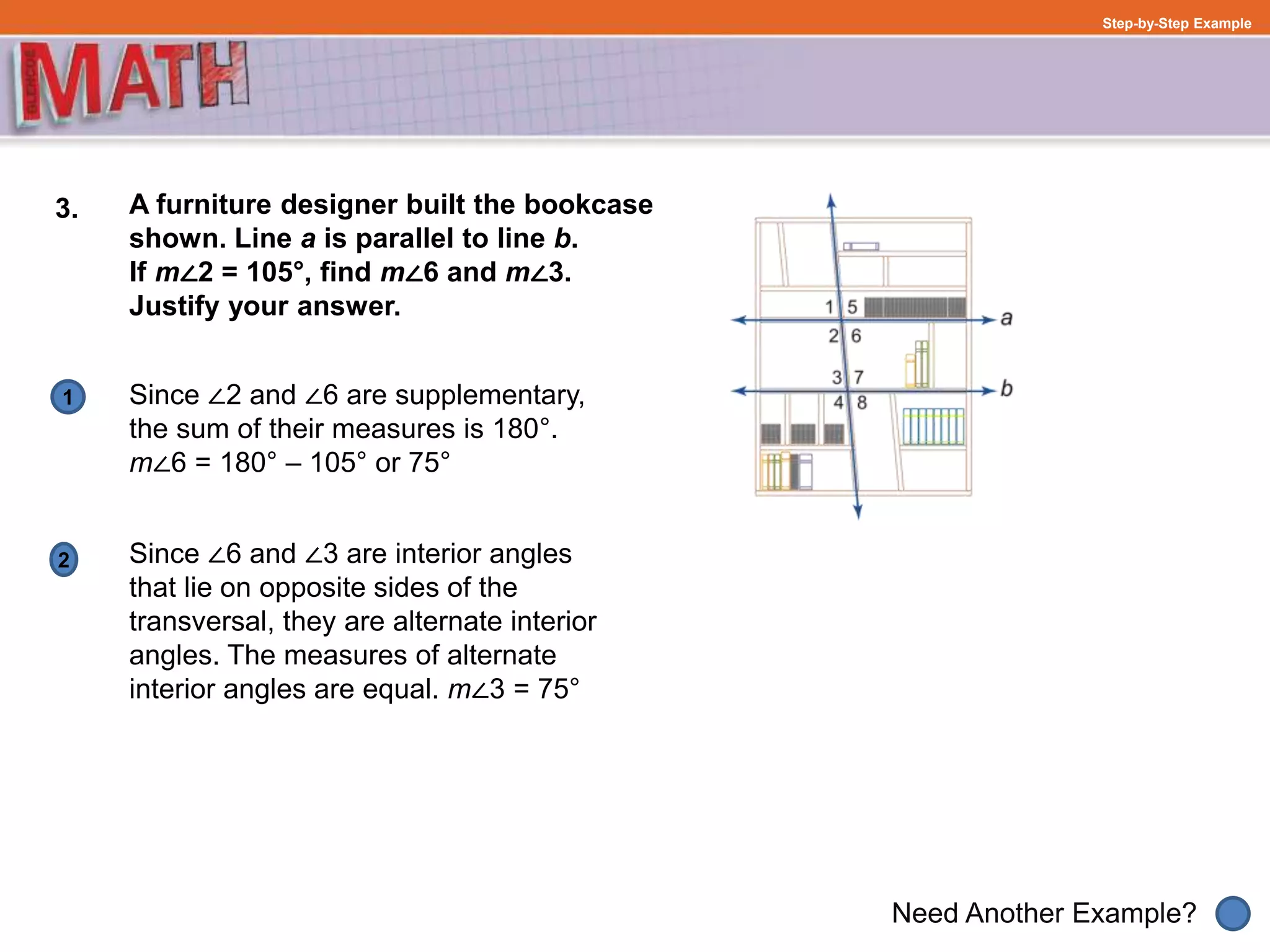
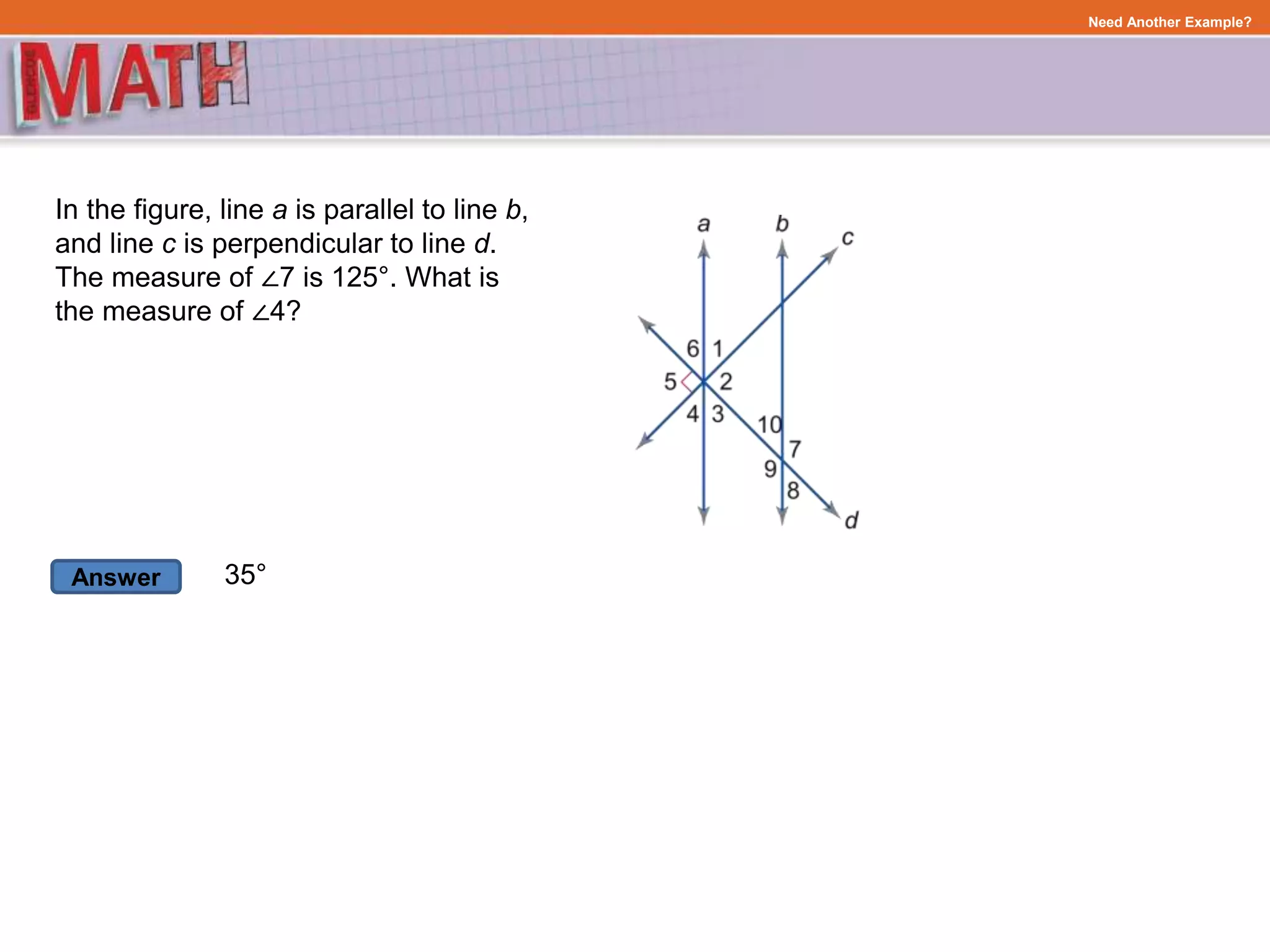
This document discusses classifying angles formed when parallel lines are cut by a transversal. It defines key terms like alternate interior angles, alternate exterior angles, and corresponding angles. It then provides examples of classifying angle pairs based on their relationship. Sample problems are worked through, applying the concepts to find missing angle measures by justifying answers using angle properties of parallel lines cut by a transversal.

1. Course 3, Lesson 5-1
1. Describe a situation that could be
represented by the graph.
2. The graph shows the relationship between
a person’s annual income and age.
Write a statement about what happens
to the income as age increases.

2. Course 3, Lesson 5-1
ANSWERS
1. Sample answer: A van frequently stops to pick up
passengers.
2. The income is increasing.

3. HOW can algebraic concepts be
applied to geometry?
Geometry
Course 3, Lesson 5-1

4. Course 3, Lesson 5-1 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and
Council of Chief State School Officers. All rights reserved.
Geometry
• 8.G.5
Use informal arguments to establish facts about the angle sum and
exterior angle of triangles, about the angles created when parallel lines
are cut by a transversal, and the angle-angle criterion for similarity of
triangles.
Mathematical Practices
1 Make sense of problems and persevere in solving them.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.

5. To
• classify the angles formed when two
lines are cut by a transversal,
• find missing angle measures when two
parallel lines are cut by a transversal
Course 3, Lesson 5-1
Geometry

6. Symbol
• perpendicular lines
• parallel lines
• transversal
• interior angles
• exterior angles
• alternate interior angles
• alternate exterior angles
• corresponding angles
• m1: the measure of  1
Course 3, Lesson 5-1
Geometry

7. Course 3, Lesson 5-1
Geometry
A line that intersects two or more lines is called a
, and eight angles are formed.transversal
Interior angles
Exterior angles
Alternate interior angles
Alternate exterior angles
Corresponding angles
lie inside the lines.
Examples: 3, 4, 5, 6  
lie outside the lines
Examples: 1, 2, 7, 8   
are interior angles that lie on opposite sides of the
transversal. When the lines are parallel, their measures are equal.
Examples: 4 6; m 3 5m m m     
are exterior angles that lie on opposite sides of
the transversal. When the lines are parallel, their measures are equal.
Examples: 1 7; 2 8m m m m     
are those angles that are in the same position on the two
lines in relation to the transversal. When the lines are parallel, their measures are
equal. Examples: 1 5; 2 6; 4 8; 3 7m m m m m m m m           

8. 1
Need Another Example?
Step-by-Step Example
1. Classify the pair of angles in the figure
as alternate interior, alternate exterior,
or corresponding.
∠1 and ∠7
∠1 and ∠7 are exterior angles that lie on
opposite sides of the transversal. They
are alternate exterior angles.

9. Answer
Need Another Example?
Classify the pair of angles as alternate interior,
alternate exterior, or corresponding.
∠3 and ∠7
corresponding

10. 1
Need Another Example?
Step-by-Step Example
2. Classify the pair of angles in the figure
as alternate interior, alternate exterior,
or corresponding.
∠2 and ∠6
∠2 and ∠6 are in the same position on the two
lines. They are corresponding angles.

11. Answer
Need Another Example?
Classify the pair of angles as alternate interior,
alternate exterior, or corresponding.
∠2 and ∠8
alternate interior

12. 1
Need Another Example?
Step-by-Step Example
3. A furniture designer built the bookcase
shown. Line a is parallel to line b.
If m∠2 = 105°, find m∠6 and m∠3.
Justify your answer.
Since ∠2 and ∠6 are supplementary,
the sum of their measures is 180°.
m∠6 = 180° – 105° or 75°
2 Since ∠6 and ∠3 are interior angles
that lie on opposite sides of the
transversal, they are alternate interior
angles. The measures of alternate
interior angles are equal. m∠3 = 75°

13. Answer
Need Another Example?
Mr. Adams installed the gate
shown. Line c is parallel to line
d. If m∠4 = 40°, find m∠6 and
m∠7. Justify your answer.
m∠6 = 40° and m∠7 = 140°; Sample answer:
∠4 and ∠6 are alternate interior angles, so they
are congruent. ∠6 and ∠7 are supplementary.
Since m∠6 = 40°, m∠7 = 140°.

14. 1
Need Another Example?
2
3
4
Step-by-Step Example
4. In the figure, line m is parallel to
line n, and line q is perpendicular
to line p. The measure of ∠1 is
40°. What is the measure of ∠7?
Since ∠1 and ∠6 are alternate
exterior angles, m∠6 = 40°.
40 + 90 + m∠7 = 180
Since ∠6, ∠7, and ∠8 form a straight line,
the sum of their measures is 180°.
So, m∠7 is 50°.

15. Answer
Need Another Example?
In the figure, line a is parallel to line b,
and line c is perpendicular to line d.
The measure of ∠7 is 125°. What is
the measure of ∠4?
35°

16. How did what you learned
today help you answer the
HOW can algebraic concepts be applied
to geometry?
Course 3, Lesson 5-1
Geometry

17. How did what you learned
today help you answer the
HOW can algebraic concepts be applied
to geometry?
Course 3, Lesson 5-1
Geometry
Sample answers:
• When two parallel lines are cut by a transversal,
analyze the figure to determine missing measures.
• Write and solve an equation to find the missing
measures.

18. Describe the pairs of
congruent angles in a set of
parallel lines cut by a
transversal.
Course 3, Lesson 5-1
Ratios and Proportional RelationshipsFunctionsGeometry