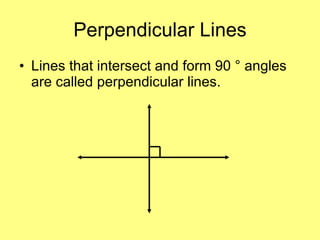
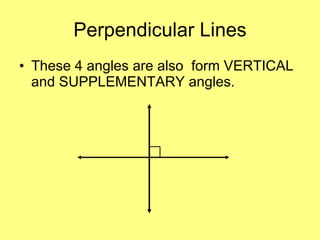
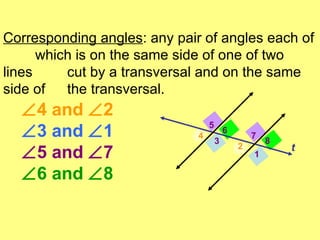
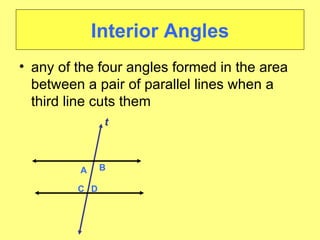
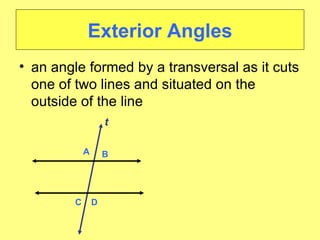
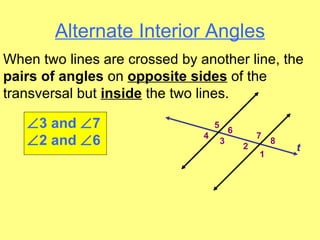
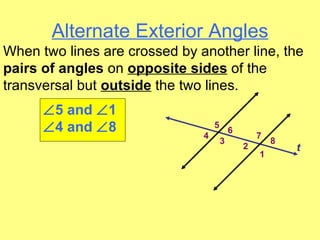
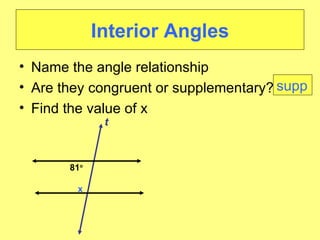
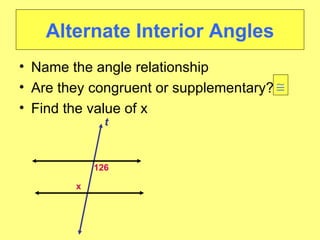
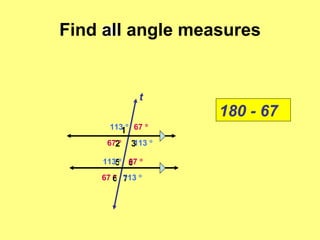
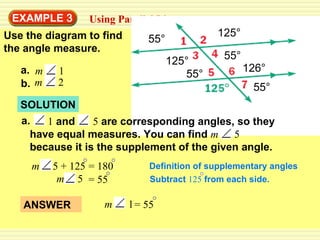
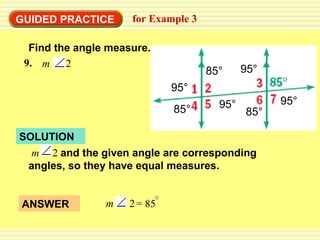
This document contains lesson materials on lines and angles including: - Solving two equations involving variables w and v - Vocabulary terms related to lines and angles - Identifying different angle relationships (corresponding angles, interior angles, etc.) when lines are cut by a transversal - Worked examples of finding missing angle measures using properties of parallel lines

1. Lesson 8.1 , For use with pages 403-408 Solve the equation. 1. 7 w = 56 2. = 21 v 3

2. Lesson 8.1 , For use with pages 403-408 Solve the equation. 1. 7 w = 56 ANSWER 8 ANSWER 63 2. = 21 v 3

3. Chapter 8.1 Lines and Angles

6. 1 2 3 4 5 6 7 8 t  4 and  2  3 and  1  5 and  7  6 and  8 Corresponding angles : any pair of angles each of which is on the same side of one of two lines cut by a transversal and on the same side of the transversal.

11. Alternate Interior Angles  3 and  7  2 and  6 1 2 3 4 5 6 7 8 t When two lines are crossed by another line, the pairs of angles on opposite sides of the transversal but inside the two lines.

13. Alternate Exterior Angles  5 and  1  4 and  8 1 2 3 4 5 6 7 8 t When two lines are crossed by another line, the pairs of angles on opposite sides of the transversal but outside the two lines.

16. Find all angle measures 1 67  3 t 113  180 - 67 2 5 6 7 8 67  67  67  113  113  113 

21. SOLUTION EXAMPLE 3 Using Parallel Lines Use the diagram to find the angle measure. Definition of supplementary angles 55° 125° 125° 55° 55° 126° 55° a. m 1 b. m 2 a. 1 and 5 are corresponding angles, so they have equal measures. You can find m 5 because it is the supplement of the given angle. m 5 = 55 Subtract 125 from each side. ANSWER m 1 = 55 m 5 + 125 = 180

22. EXAMPLE 3 Using Parallel Lines b. 2 and the given angle are alternate exterior angles, so they have equal measures. ANSWER m 2 = 125

23. GUIDED PRACTICE for Example 3 SOLUTION 85° 95° 95° 85° 95° 85° 95° m 2 and the given angle are corresponding angles, so they have equal measures. ANSWER m 2 = 85 9. m 2 Find the angle measure.