This document defines key terms and concepts related to parallel lines and transversals, including: - A transversal is a line that intersects two other lines at two different points. - Interior angles are formed between the two lines, while exterior angles are outside the lines. - Alternate interior angles, corresponding angles, and other angle relationships are defined. - Examples demonstrate identifying angle relationships and using properties of parallel lines to calculate unknown angle measures.

1. SECTION 2-7
Parallel Lines and Transversals

2. ESSENTIAL
QUESTIONS
How do you identify the relationships between two lines or
two planes?
How do you name angle pairs formed by parallel lines and
transversals?

3. VOCABULARY
1. Transversal:
2. Interior Angles:
3. Exterior Angles:
4. Consecutive Interior Angles:

4. VOCABULARY
1. Transversal: A line that intersects two other coplanar lines at
two different points
2. Interior Angles:
3. Exterior Angles:
4. Consecutive Interior Angles:

5. VOCABULARY
1. Transversal: A line that intersects two other coplanar lines at
two different points
2. Interior Angles: Angles that are formed in the region between
two lines being intersected by a transversal
3. Exterior Angles:
4. Consecutive Interior Angles:

6. VOCABULARY
1. Transversal: A line that intersects two other coplanar lines at
two different points
2. Interior Angles: Angles that are formed in the region between
two lines being intersected by a transversal
3. Exterior Angles: Angles that are formed in the region outside of
the two lines being intersected by a transversal
4. Consecutive Interior Angles:

7. VOCABULARY
1. Transversal: A line that intersects two other coplanar lines at
two different points
2. Interior Angles: Angles that are formed in the region between
two lines being intersected by a transversal
3. Exterior Angles: Angles that are formed in the region outside of
the two lines being intersected by a transversal
4. Consecutive Interior Angles: Interior angles that are on the
same side of the transversal, thus being “next” to each other

8. VOCABULARY
5. Alternate Interior Angles:
6. Alternate Exterior Angles:
7. Corresponding Angles:
8. Parallel Lines:

9. VOCABULARY
5. Alternate Interior Angles: Nonadjacent interior angles that are
on opposite sides of the transversal
6. Alternate Exterior Angles:
7. Corresponding Angles:
8. Parallel Lines:

10. VOCABULARY
5. Alternate Interior Angles: Nonadjacent interior angles that are
on opposite sides of the transversal
6. Alternate Exterior Angles:
7. Corresponding Angles:
8. Parallel Lines:
Nonadjacent exterior angles that are
on opposite sides of the transversal

11. VOCABULARY
5. Alternate Interior Angles: Nonadjacent interior angles that are
on opposite sides of the transversal
6. Alternate Exterior Angles:
7. Corresponding Angles:
8. Parallel Lines:
Nonadjacent exterior angles that are
on opposite sides of the transversal
Angles that are on the same side of the
transversal and on the same side of the lines being intersected
by the transversal; these angles have the same position

12. VOCABULARY
5. Alternate Interior Angles: Nonadjacent interior angles that are
on opposite sides of the transversal
6. Alternate Exterior Angles:
7. Corresponding Angles:
8. Parallel Lines: Two or more lines in the same plane that do not
intersect
Nonadjacent exterior angles that are
on opposite sides of the transversal
Angles that are on the same side of the
transversal and on the same side of the lines being intersected
by the transversal; these angles have the same position

13. VOCABULARY
9. Skew Lines:
10. Parallel Planes:

14. VOCABULARY
9. Skew Lines: Two or more lines that are in different planes and
do not intersect
10. Parallel Planes:

15. VOCABULARY
9. Skew Lines: Two or more lines that are in different planes and
do not intersect
10. Parallel Planes: Two or more planes that do not intersect

16. EXAMPLE 1
Identify each of the following using the box.
a. All segments parallel to BC
b. A segment that is skew to EH
c. A plane that is parallel to plane ABG

17. EXAMPLE 1
Identify each of the following using the box.
a. All segments parallel to BC
FG, AD, EH
b. A segment that is skew to EH
c. A plane that is parallel to plane ABG

18. EXAMPLE 1
Identify each of the following using the box.
a. All segments parallel to BC
FG, AD, EH
b. A segment that is skew to EH
DC, CF, AB, or BG
c. A plane that is parallel to plane ABG

19. EXAMPLE 1
Identify each of the following using the box.
a. All segments parallel to BC
FG, AD, EH
b. A segment that is skew to EH
DC, CF, AB, or BG
c. A plane that is parallel to plane ABG
Plane DEC

20. EXAMPLE 2
Refer to the figure below. Classify the relationship between
each pair of angles as alternate interior, alternate exterior,
corresponding, or consecutive interior angles.
a. ∠2 and ∠6 b. ∠1 and ∠7

21. EXAMPLE 2
Refer to the figure below. Classify the relationship between
each pair of angles as alternate interior, alternate exterior,
corresponding, or consecutive interior angles.
a. ∠2 and ∠6 b. ∠1 and ∠7
Corresponding Angles

22. EXAMPLE 2
Refer to the figure below. Classify the relationship between
each pair of angles as alternate interior, alternate exterior,
corresponding, or consecutive interior angles.
a. ∠2 and ∠6 b. ∠1 and ∠7
Corresponding Angles Alternate Exterior Angles

23. EXAMPLE 2
Refer to the figure below. Classify the relationship between
each pair of angles as alternate interior, alternate exterior,
corresponding, or consecutive interior angles.
c. ∠3 and ∠8 d. ∠3 and ∠5

24. EXAMPLE 2
Refer to the figure below. Classify the relationship between
each pair of angles as alternate interior, alternate exterior,
corresponding, or consecutive interior angles.
c. ∠3 and ∠8 d. ∠3 and ∠5
Consecutive Interior Angles

25. EXAMPLE 2
Refer to the figure below. Classify the relationship between
each pair of angles as alternate interior, alternate exterior,
corresponding, or consecutive interior angles.
c. ∠3 and ∠8 d. ∠3 and ∠5
Consecutive Interior Angles Alternate Interior Angles

26. EXAMPLE 3
The driveways at a bus station are shown. Identify the
transversal connecting each pair of angles in the figure. Then
classify the relationship between each pair of angles.
a. ∠1 and ∠2 b. ∠2 and ∠3

27. EXAMPLE 3
The driveways at a bus station are shown. Identify the
transversal connecting each pair of angles in the figure. Then
classify the relationship between each pair of angles.
a. ∠1 and ∠2 b. ∠2 and ∠3
v; Corresponding

28. EXAMPLE 3
The driveways at a bus station are shown. Identify the
transversal connecting each pair of angles in the figure. Then
classify the relationship between each pair of angles.
a. ∠1 and ∠2 b. ∠2 and ∠3
v; Corresponding v; Alternate Interior

29. EXAMPLE 3
The driveways at a bus station are shown. Identify the
transversal connecting each pair of angles in the figure. Then
classify the relationship between each pair of angles.
c. ∠4 and ∠5

30. EXAMPLE 3
The driveways at a bus station are shown. Identify the
transversal connecting each pair of angles in the figure. Then
classify the relationship between each pair of angles.
c. ∠4 and ∠5
y; Consecutive Interior

31. POSTULATES AND THEOREMS
CORRESPONDING ANGLES POSTULATE

32. POSTULATES AND THEOREMS
CORRESPONDING ANGLES POSTULATE
IF TWO PARALLEL LINES ARE CUT BY A
TRANSVERSAL, THEN EACH PAIR OF
CORRESPONDING ANGLES IS CONGRUENT.

33. POSTULATES AND THEOREMS
CORRESPONDING ANGLES POSTULATE
IF TWO PARALLEL LINES ARE CUT BY A
TRANSVERSAL, THEN EACH PAIR OF
CORRESPONDING ANGLES IS CONGRUENT.
∠1 ≅ ∠5

34. POSTULATES AND THEOREMS
ALTERNATE INTERIOR ANGLES THEOREM

35. POSTULATES AND THEOREMS
ALTERNATE INTERIOR ANGLES THEOREM
IF TWO PARALLEL LINES ARE CUT BY A
TRANSVERSAL, THEN EACH PAIR OF
ALTERNATE INTERIOR ANGLES IS
CONGRUENT.

36. POSTULATES AND THEOREMS
ALTERNATE INTERIOR ANGLES THEOREM
IF TWO PARALLEL LINES ARE CUT BY A
TRANSVERSAL, THEN EACH PAIR OF
ALTERNATE INTERIOR ANGLES IS
CONGRUENT.
∠4 ≅ ∠6

37. POSTULATES AND THEOREMS
CONSECUTIVE INTERIOR ANGLES THEOREM

38. POSTULATES AND THEOREMS
CONSECUTIVE INTERIOR ANGLES THEOREM
IF TWO PARALLEL LINES ARE CUT BY A
TRANSVERSAL, THEN EACH PAIR OF
CONSECUTIVE INTERIOR ANGLES IS
SUPPLEMENTARY.

39. POSTULATES AND THEOREMS
CONSECUTIVE INTERIOR ANGLES THEOREM
IF TWO PARALLEL LINES ARE CUT BY A
TRANSVERSAL, THEN EACH PAIR OF
CONSECUTIVE INTERIOR ANGLES IS
SUPPLEMENTARY.
∠4 AND ∠5 ARE SUPPLEMENTARY

40. POSTULATES AND THEOREMS
ALTERNATE EXTERIOR ANGLES THEOREM

41. POSTULATES AND THEOREMS
ALTERNATE EXTERIOR ANGLES THEOREM
IF TWO PARALLEL LINES ARE CUT BY A
TRANSVERSAL, THEN EACH PAIR OF
ALTERNATE EXTERIOR ANGLES IS
CONGRUENT.

42. POSTULATES AND THEOREMS
ALTERNATE EXTERIOR ANGLES THEOREM
IF TWO PARALLEL LINES ARE CUT BY A
TRANSVERSAL, THEN EACH PAIR OF
ALTERNATE EXTERIOR ANGLES IS
CONGRUENT.
∠2 ≅ ∠7

43. EXAMPLE 4
IN THE FIGURE, m∠4 = 51°. FIND THE MEASURE
OF EACH ANGLE. GIVE A JUSTIFICATION TO
YOUR ANSWER.
a. m∠2
b. m∠3
c. m∠6

44. EXAMPLE 4
IN THE FIGURE, m∠4 = 51°. FIND THE MEASURE
OF EACH ANGLE. GIVE A JUSTIFICATION TO
YOUR ANSWER.
a. m∠2
51°; VERTICAL ANGLES
THM. WITH ∠4
b. m∠3
c. m∠6

45. EXAMPLE 4
IN THE FIGURE, m∠4 = 51°. FIND THE MEASURE
OF EACH ANGLE. GIVE A JUSTIFICATION TO
YOUR ANSWER.
a. m∠2
51°; VERTICAL ANGLES
THM. WITH ∠4
b. m∠3
129°; SUPPLEMENTARY THM. WITH ∠4
c. m∠6

46. EXAMPLE 4
IN THE FIGURE, m∠4 = 51°. FIND THE MEASURE
OF EACH ANGLE. GIVE A JUSTIFICATION TO
YOUR ANSWER.
a. m∠2
51°; VERTICAL ANGLES
THM. WITH ∠4
b. m∠3
129°; SUPPLEMENTARY THM. WITH ∠4
c. m∠6
51°; ALTERNATE INTERIOR ANGLES THM.
WITH ∠4

47. EXAMPLE 5
USE THE FIGURE, IN WHICH a||b, m∠2 = 125°,
AND c||d||e, TO FIND THE MEASURE OF EACH
NUMBERED ANGLE. PROVIDE A REASON FOR
THE ANSWER FOR EACH MEASURE.

48. EXAMPLE 5
USE THE FIGURE, IN WHICH a||b, m∠2 = 125°,
AND c||d||e, TO FIND THE MEASURE OF EACH
NUMBERED ANGLE. PROVIDE A REASON FOR
THE ANSWER FOR EACH MEASURE.
m∠1 = 125°; VERTICAL
ANGLES THM. WITH ∠2

49. EXAMPLE 5
USE THE FIGURE, IN WHICH a||b, m∠2 = 125°,
AND c||d||e, TO FIND THE MEASURE OF EACH
NUMBERED ANGLE. PROVIDE A REASON FOR
THE ANSWER FOR EACH MEASURE.
m∠1 = 125°; VERTICAL
ANGLES THM. WITH ∠2
m∠3 = 55°; CONSECUTIVE
INTERIOR ANGLES THM. WITH ∠2

50. EXAMPLE 5
USE THE FIGURE, IN WHICH a||b, m∠2 = 125°,
AND c||d||e, TO FIND THE MEASURE OF EACH
NUMBERED ANGLE. PROVIDE A REASON FOR
THE ANSWER FOR EACH MEASURE.
m∠1 = 125°; VERTICAL
ANGLES THM. WITH ∠2
m∠3 = 55°; CONSECUTIVE
INTERIOR ANGLES THM. WITH ∠2
m∠4 = 125°; CONSECUTIVE
INTERIOR ANGLES THM. WITH ∠3

51. EXAMPLE 5
USE THE FIGURE, IN WHICH a||b, m∠2 = 125°,
AND c||d||e, TO FIND THE MEASURE OF EACH
NUMBERED ANGLE. PROVIDE A REASON FOR
THE ANSWER FOR EACH MEASURE.
m∠1 = 125°; VERTICAL
ANGLES THM. WITH ∠2
m∠3 = 55°; CONSECUTIVE
INTERIOR ANGLES THM. WITH ∠2
m∠4 = 125°; CONSECUTIVE
INTERIOR ANGLES THM. WITH ∠3
m∠5 = 55°; SUPPLEMENTARY ANGLES THM. WITH ∠4

52. EXAMPLE 6
USE THE FIGURE TO FIND THE INDICATED
VARIABLE. EXPLAIN YOUR REASONING.
a. IF m∠2 = (2x ­ 10)° AND
m∠6 = (x + 15)°, FIND x.

53. EXAMPLE 6
USE THE FIGURE TO FIND THE INDICATED
VARIABLE. EXPLAIN YOUR REASONING.
a. IF m∠2 = (2x ­ 10)° AND
m∠6 = (x + 15)°, FIND x.
2x ­ 10 = x + 15

54. EXAMPLE 6
USE THE FIGURE TO FIND THE INDICATED
VARIABLE. EXPLAIN YOUR REASONING.
a. IF m∠2 = (2x ­ 10)° AND
m∠6 = (x + 15)°, FIND x.
2x ­ 10 = x + 15
­x ­x

55. EXAMPLE 6
USE THE FIGURE TO FIND THE INDICATED
VARIABLE. EXPLAIN YOUR REASONING.
a. IF m∠2 = (2x ­ 10)° AND
m∠6 = (x + 15)°, FIND x.
2x ­ 10 = x + 15
­x ­x +10+10

56. EXAMPLE 6
USE THE FIGURE TO FIND THE INDICATED
VARIABLE. EXPLAIN YOUR REASONING.
a. IF m∠2 = (2x ­ 10)° AND
m∠6 = (x + 15)°, FIND x.
2x ­ 10 = x + 15
­x ­x +10+10
x = 25

57. EXAMPLE 6
USE THE FIGURE TO FIND THE INDICATED
VARIABLE. EXPLAIN YOUR REASONING.
a. IF m∠2 = (2x ­ 10)° AND
m∠6 = (x + 15)°, FIND x.
2x ­ 10 = x + 15
­x ­x +10+10
x = 25
SINCE THE ANGLES ARE CORRESPONDING, THEY
ARE CONGRUENT BY THE CORRESPONDING
ANGLES POSTULATE, SO THEIR MEASURES ARE
EQUA BY THE DEF. OF CONGRUENT ANGLES.

58. EXAMPLE 6
USE THE FIGURE TO FIND THE INDICATED
VARIABLE. EXPLAIN YOUR REASONING.
b. IF m∠7 = [4(y ­ 25)]° AND
m∠1 = (4y)°, FIND y.

59. EXAMPLE 6
USE THE FIGURE TO FIND THE INDICATED
VARIABLE. EXPLAIN YOUR REASONING.
b. IF m∠7 = [4(y ­ 25)]° AND
m∠1 = (4y)°, FIND y.
4(y ­ 25) + 4y = 180

60. EXAMPLE 6
USE THE FIGURE TO FIND THE INDICATED
VARIABLE. EXPLAIN YOUR REASONING.
b. IF m∠7 = [4(y ­ 25)]° AND
m∠1 = (4y)°, FIND y.
4(y ­ 25) + 4y = 180
4y ­ 100 + 4y = 180

61. EXAMPLE 6
USE THE FIGURE TO FIND THE INDICATED
VARIABLE. EXPLAIN YOUR REASONING.
b. IF m∠7 = [4(y ­ 25)]° AND
m∠1 = (4y)°, FIND y.
4(y ­ 25) + 4y = 180
4y ­ 100 + 4y = 180
8y ­ 100 = 180

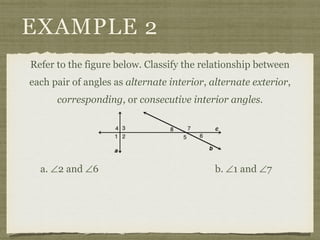
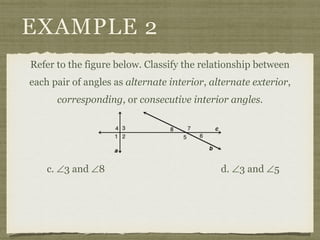
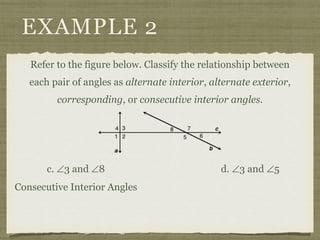
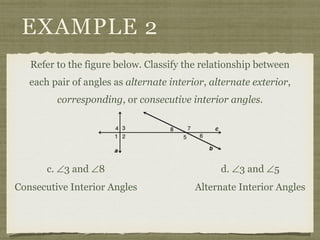
62. EXAMPLE 6
USE THE FIGURE TO FIND THE INDICATED
VARIABLE. EXPLAIN YOUR REASONING.
b. IF m∠7 = [4(y ­ 25)]° AND
m∠1 = (4y)°, FIND y.
4(y ­ 25) + 4y = 180
4y ­ 100 + 4y = 180
8y ­ 100 = 180
8y = 280

63. EXAMPLE 6
USE THE FIGURE TO FIND THE INDICATED
VARIABLE. EXPLAIN YOUR REASONING.
b. IF m∠7 = [4(y ­ 25)]° AND
m∠1 = (4y)°, FIND y.
4(y ­ 25) + 4y = 180
4y ­ 100 + 4y = 180
8y ­ 100 = 180
8y = 280
y = 35