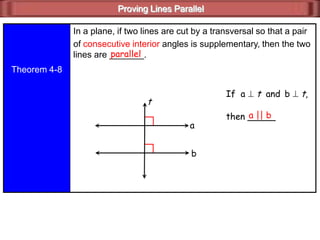
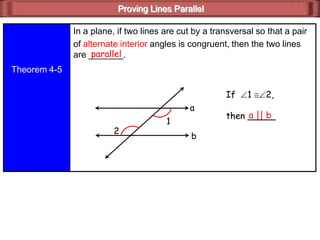
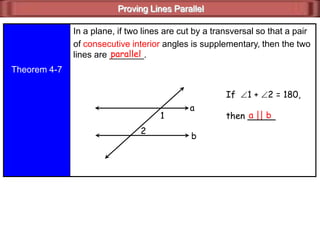
This document discusses ways to prove that two lines are parallel using postulates and theorems about angles formed when lines are cut by a transversal. Specifically, it states that two lines are parallel if: - A pair of corresponding angles is congruent - A pair of alternate interior angles is congruent - A pair of alternate exterior angles is congruent - A pair of consecutive interior angles is supplementary - The two lines are perpendicular to a third line Examples are provided to demonstrate applying these rules to identify parallel lines and find values that prove lines are parallel.

1. Proving Lines Parallel
You will learn to identify conditions that produce parallel lines.
Reminder: In Chapter 1, we discussed “if-then” statements (pg. 24).
Within those statements, we identified the “__________” and the
“_________”.
hypothesis
conclusion
I said then that in mathematics, we only use the term
“if and only if”
if the converse of the statement is true.

2. Proving Lines Parallel
Postulate 4 – 1 (pg. 156):
IF ___________________________________,
THEN ________________________________________.
two parallel lines are cut by a transversal
each pair of corresponding angles is congruent
The postulates used in 4 - 4 are the converse of postulates that you already
know. COOL, HUH?
4 – 4, Postulate 4 – 2 (pg. 162):
IF ________________________________________,
THEN ____________________________________.
each pair of corresponding angles is congruent
two parallel lines are cut by a transversal

3. Proving Lines Parallel
Postulate 4-2
In a plane, if two lines are cut by a transversal so that a pair
of corresponding angles is congruent, then the lines are
_______.parallel
If 1 2,
then _____a || b
1
2
a
b

4. Proving Lines Parallel
Theorem 4-5
In a plane, if two lines are cut by a transversal so that a pair
of alternate interior angles is congruent, then the two lines
are _______.parallel
If 1 2,
then _____a || b
1
2
a
b

5. Proving Lines Parallel
Theorem 4-6
In a plane, if two lines are cut by a transversal so that a pair
of alternate exterior angles is congruent, then the two lines
are _______.parallel
If 1 2,
then _____a || b
1
2
a
b

6. Proving Lines Parallel
Theorem 4-7
In a plane, if two lines are cut by a transversal so that a pair
of consecutive interior angles is supplementary, then the two
lines are _______.parallel
If 1 + 2 = 180,
then _____a || b1
2
a
b

7. Proving Lines Parallel
Theorem 4-8
In a plane, if two lines are cut by a transversal so that a pair
of consecutive interior angles is supplementary, then the two
lines are _______.parallel
If a t and b t,
then _____a || b
a
b
t

8. Proving Lines Parallel
Concept
Summary
We now have five ways to prove that two lines are parallel.
Show that a pair of corresponding angles is congruent.
Show that a pair of alternate interior angles is congruent.
Show that a pair of alternate exterior angles is congruent.
Show that a pair of consecutive interior angles is
supplementary.
Show that two lines in a plane are perpendicular to a
third line.

9. Proving Lines Parallel
Identify any parallel segments. Explain your reasoning.
G
A
Y
D
R
90°
90°
therefore,
GAlar toperpendicubothareand RDGY
8.-4TheorembyRDGY

10. Proving Lines Parallel
EB
ST
(6x - 26)° (2x + 10)°
(5x + 2)°
Find the value for x so BE || TS.
ES is a transversal for BE and TS.
BES and EST are _________________ angles.consecutive interior
If m BES + m EST = 180, then
BE || TS by Theorem 4 – 7.
m BES + m EST = 180
(2x + 10) + (5x + 2) = 180
7x + 12 = 180
7x = 168
x = 24
Thus, if x = 24, then BE || TS.