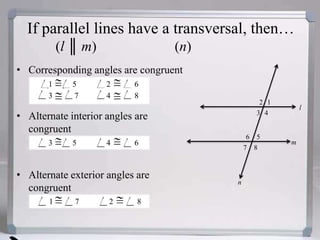
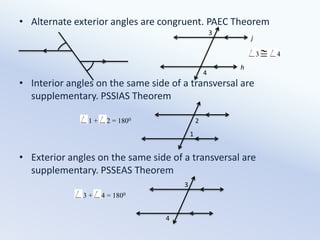
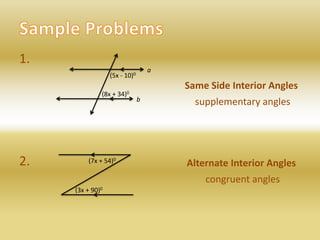
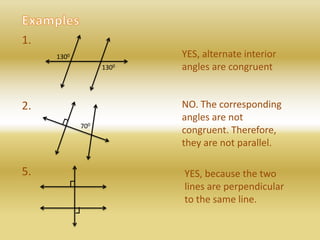
If parallel lines are cut by a transversal, then:
- Corresponding angles are congruent
- Alternate interior angles are congruent
- Alternate exterior angles are congruent
- Interior angles on the same side of the transversal are supplementary
- Exterior angles on the same side of the transversal are supplementary