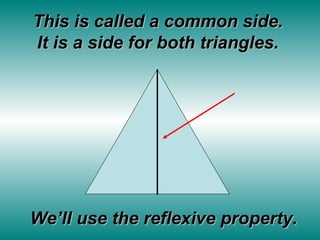
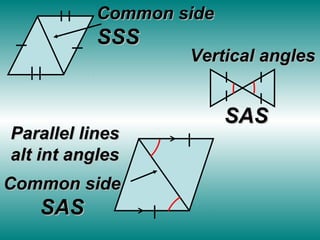
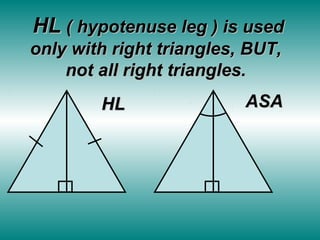
The document outlines methods for proving triangle congruence, emphasizing that proving all corresponding angles and sides do not require exhaustive evaluation. It introduces five shortcuts: SSS, SAS, ASA, AAS, and HL, with explanations and examples for each. Additionally, it highlights the importance of using given information, properties, and definitions in proofs.