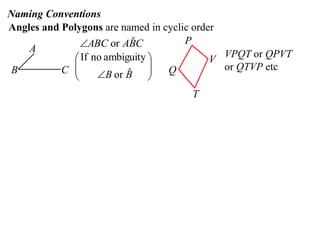
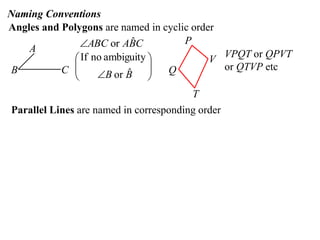
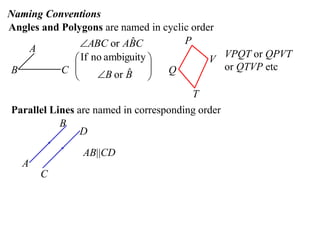
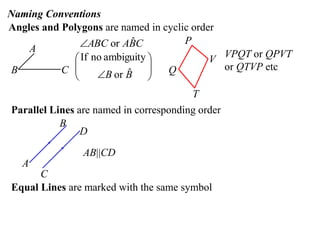
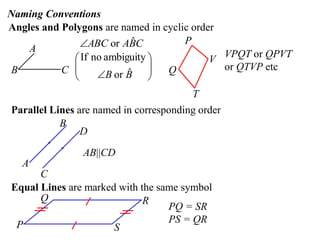
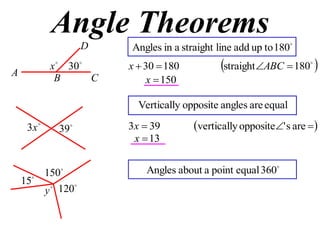
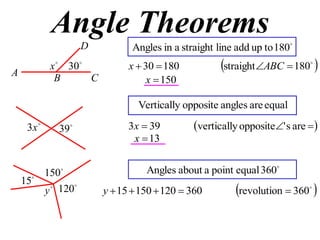
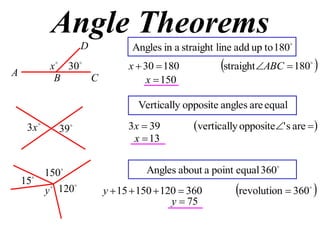
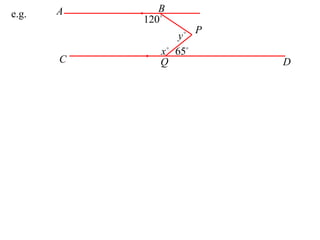
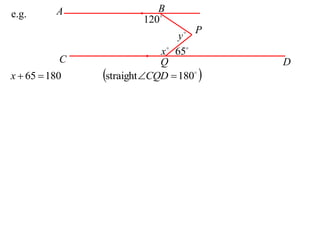
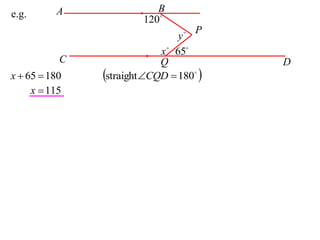
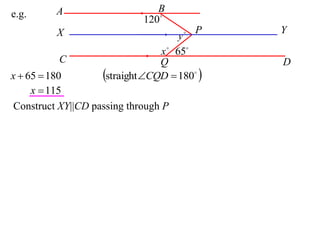
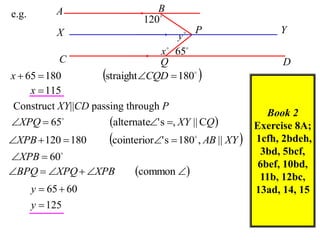
The document discusses key concepts in Euclidean geometry including definitions, notation, terminology, naming conventions, angle theorems, and constructing proofs. It defines parallel lines, perpendicular lines, congruent lines, and similar lines using notation symbols. It provides examples of naming angles, polygons, and parallel lines in a consistent cyclic order. It also outlines the steps and logical structure required to properly construct geometric proofs.

1. Euclidean Geometry

2. Euclidean Geometry
Geometry Definitions
Notation
toparallelis|| 

3. Euclidean Geometry
Geometry Definitions
Notation
toparallelis|| 
lar toperpendicuis

4. Euclidean Geometry
Geometry Definitions
Notation
toparallelis|| 
lar toperpendicuis
tocongruentis

5. Euclidean Geometry
Geometry Definitions
Notation
toparallelis|| 
lar toperpendicuis
tocongruentis
similar tois||| 

6. Euclidean Geometry
Geometry Definitions
Notation
toparallelis|| 
lar toperpendicuis
tocongruentis
similar tois||| 
therefore

7. Euclidean Geometry
Geometry Definitions
Notation
toparallelis|| 
lar toperpendicuis
tocongruentis
similar tois||| 
therefore
because

8. Euclidean Geometry
Geometry Definitions
Notation
Terminology
toparallelis|| 
lar toperpendicuis
tocongruentis
similar tois||| 
therefore
because
produced – the line is extended

9. Euclidean Geometry
Geometry Definitions
Notation
Terminology
toparallelis|| 
lar toperpendicuis
tocongruentis
similar tois||| 
therefore
because
produced – the line is extended
X Y
XY is produced to A
A

10. Euclidean Geometry
Geometry Definitions
Notation
Terminology
toparallelis|| 
lar toperpendicuis
tocongruentis
similar tois||| 
therefore
because
produced – the line is extended
X Y
XY is produced to A
A
YX is produced to B
B

11. Euclidean Geometry
Geometry Definitions
Notation
Terminology
toparallelis|| 
lar toperpendicuis
tocongruentis
similar tois||| 
therefore
because
produced – the line is extended
X Y
XY is produced to A
A
YX is produced to B
B
foot – the base or the bottom

12. Euclidean Geometry
Geometry Definitions
Notation
Terminology
toparallelis|| 
lar toperpendicuis
tocongruentis
similar tois||| 
therefore
because
produced – the line is extended
X Y
XY is produced to A
A
YX is produced to B
B
foot – the base or the bottom
A
B
CD
B is the foot of the perpendicular

13. Euclidean Geometry
Geometry Definitions
Notation
Terminology
toparallelis|| 
lar toperpendicuis
tocongruentis
similar tois||| 
therefore
because
produced – the line is extended
X Y
XY is produced to A
A
YX is produced to B
B
foot – the base or the bottom
A
B
CD
B is the foot of the perpendicular
collinear – the points lie on the same line

14. Euclidean Geometry
Geometry Definitions
Notation
Terminology
toparallelis|| 
lar toperpendicuis
tocongruentis
similar tois||| 
therefore
because
produced – the line is extended
X Y
XY is produced to A
A
YX is produced to B
B
foot – the base or the bottom
A
B
CD
B is the foot of the perpendicular
collinear – the points lie on the same line
concurrent – the lines intersect at the same
point

15. Euclidean Geometry
Geometry Definitions
Notation
Terminology
toparallelis|| 
lar toperpendicuis
tocongruentis
similar tois||| 
therefore
because
produced – the line is extended
X Y
XY is produced to A
A
YX is produced to B
B
foot – the base or the bottom
A
B
CD
B is the foot of the perpendicular
collinear – the points lie on the same line
concurrent – the lines intersect at the same
point
transversal – a line that cuts two(or more)
other lines

16. Naming Conventions
Angles and Polygons are named in cyclic order

17. Naming Conventions
Angles and Polygons are named in cyclic order
A
B C
CBAABC ˆor






 BB ˆor
ambiguitynoIf

18. Naming Conventions
Angles and Polygons are named in cyclic order
A
B C
CBAABC ˆor






 BB ˆor
ambiguitynoIf
P
V
T
Q
VPQT or QPVT
or QTVP etc

19. Naming Conventions
Angles and Polygons are named in cyclic order
A
B C
CBAABC ˆor






 BB ˆor
ambiguitynoIf
P
V
T
Q
VPQT or QPVT
or QTVP etc
Parallel Lines are named in corresponding order

20. Naming Conventions
Angles and Polygons are named in cyclic order
A
B C
CBAABC ˆor






 BB ˆor
ambiguitynoIf
P
V
T
Q
VPQT or QPVT
or QTVP etc
Parallel Lines are named in corresponding order
A
B
C
D
AB||CD

21. Naming Conventions
Angles and Polygons are named in cyclic order
A
B C
CBAABC ˆor






 BB ˆor
ambiguitynoIf
P
V
T
Q
VPQT or QPVT
or QTVP etc
Parallel Lines are named in corresponding order
A
B
C
D
AB||CD
Equal Lines are marked with the same symbol

22. Naming Conventions
Angles and Polygons are named in cyclic order
A
B C
CBAABC ˆor






 BB ˆor
ambiguitynoIf
P
V
T
Q
VPQT or QPVT
or QTVP etc
Parallel Lines are named in corresponding order
A
B
C
D
AB||CD
Equal Lines are marked with the same symbol
P
Q R
S
PQ = SR
PS = QR

23. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;

24. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;
1. Given information, do not assume information is given, e.g. if you
are told two sides are of a triangle are equal don’t assume it is
isosceles, state that it is isosceles because two sides are equal.

25. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;
1. Given information, do not assume information is given, e.g. if you
are told two sides are of a triangle are equal don’t assume it is
isosceles, state that it is isosceles because two sides are equal.
2. Construction of new lines, state clearly your construction so that
anyone reading your proof could recreate the construction.

26. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;
1. Given information, do not assume information is given, e.g. if you
are told two sides are of a triangle are equal don’t assume it is
isosceles, state that it is isosceles because two sides are equal.
2. Construction of new lines, state clearly your construction so that
anyone reading your proof could recreate the construction.
3. A recognised geometrical theorem (or assumption), any theorem
you are using must be explicitly stated, whether it is in the algebraic
statement or the reason itself.

27. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;
1. Given information, do not assume information is given, e.g. if you
are told two sides are of a triangle are equal don’t assume it is
isosceles, state that it is isosceles because two sides are equal.
2. Construction of new lines, state clearly your construction so that
anyone reading your proof could recreate the construction.
3. A recognised geometrical theorem (or assumption), any theorem
you are using must be explicitly stated, whether it is in the algebraic
statement or the reason itself.
 180sum18012025e.g. A

28. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;
1. Given information, do not assume information is given, e.g. if you
are told two sides are of a triangle are equal don’t assume it is
isosceles, state that it is isosceles because two sides are equal.
2. Construction of new lines, state clearly your construction so that
anyone reading your proof could recreate the construction.
3. A recognised geometrical theorem (or assumption), any theorem
you are using must be explicitly stated, whether it is in the algebraic
statement or the reason itself.
 180sum18012025e.g. A
Your reasoning should be clear and concise

29. Constructing Proofs
When constructing a proof, any line that you state must be one of the
following;
1. Given information, do not assume information is given, e.g. if you
are told two sides are of a triangle are equal don’t assume it is
isosceles, state that it is isosceles because two sides are equal.
2. Construction of new lines, state clearly your construction so that
anyone reading your proof could recreate the construction.
3. A recognised geometrical theorem (or assumption), any theorem
you are using must be explicitly stated, whether it is in the algebraic
statement or the reason itself.
4. Any working out that follows from lines already stated.
 180sum18012025e.g. A
Your reasoning should be clear and concise

30. Angle Theorems

31. Angle Theorems 
180toupaddlinestraightainAngles

32. Angle Theorems
A
B C
D 
180toupaddlinestraightainAngles

x 
30

33. Angle Theorems
A
B C
D 
180toupaddlinestraightainAngles
 
180straight18030  ABCx
x 
30

34. Angle Theorems
A
B C
D 
180toupaddlinestraightainAngles
 
180straight18030  ABCx
150x

x 
30

35. Angle Theorems
A
B C
D 
180toupaddlinestraightainAngles
 
180straight18030  ABCx
150x

x 
30
equalareanglesoppositeVertically

36. Angle Theorems
A
B C
D 
180toupaddlinestraightainAngles
 
180straight18030  ABCx
150x

x 
30
equalareanglesoppositeVertically

x3 
39

37. Angle Theorems
A
B C
D 
180toupaddlinestraightainAngles
 
180straight18030  ABCx
150x

x 
30
equalareanglesoppositeVertically
  ares'oppositevertically393x
x3 
39

38. Angle Theorems
A
B C
D 
180toupaddlinestraightainAngles
 
180straight18030  ABCx
150x

x 
30
equalareanglesoppositeVertically
  ares'oppositevertically393x
13x

x3 
39

39. Angle Theorems
A
B C
D 
180toupaddlinestraightainAngles
 
180straight18030  ABCx
150x

x 
30
equalareanglesoppositeVertically
  ares'oppositevertically393x
13x

x3 
39

360equalpointaaboutAngles

40. Angle Theorems
A
B C
D 
180toupaddlinestraightainAngles
 
180straight18030  ABCx
150x

x 
30
equalareanglesoppositeVertically
  ares'oppositevertically393x
13x

x3 
39

360equalpointaaboutAngles

y

15

150

120

41. Angle Theorems
A
B C
D 
180toupaddlinestraightainAngles
 
180straight18030  ABCx
150x

x 
30
equalareanglesoppositeVertically
  ares'oppositevertically393x
13x

x3 
39

360equalpointaaboutAngles
 
360revolution36012015015 y
y

15

150

120

42. Angle Theorems
A
B C
D 
180toupaddlinestraightainAngles
 
180straight18030  ABCx
150x

x 
30
equalareanglesoppositeVertically
  ares'oppositevertically393x
13x

x3 
39

360equalpointaaboutAngles
 
360revolution36012015015 y
75y

y

15

150

120

43. Parallel Line Theorems
a
b
c
d
e
f
h
g

44. Parallel Line Theorems
a
b
c
d
e
f
h
g
Alternate angles (Z) are equal

45. Parallel Line Theorems
a
b
c
d
e
f
h
g
Alternate angles (Z) are equal
 lines||,s'alternate  fc

46. Parallel Line Theorems
a
b
c
d
e
f
h
g
Alternate angles (Z) are equal
 lines||,s'alternate  fc
ed 

47. Parallel Line Theorems
a
b
c
d
e
f
h
g
Alternate angles (Z) are equal
 lines||,s'alternate  fc
ed 
Corresponding angles (F) are equal

48. Parallel Line Theorems
a
b
c
d
e
f
h
g
Alternate angles (Z) are equal
 lines||,s'alternate  fc
ed 
Corresponding angles (F) are equal
 lines||,s'ingcorrespond  ea

49. Parallel Line Theorems
a
b
c
d
e
f
h
g
Alternate angles (Z) are equal
 lines||,s'alternate  fc
ed 
Corresponding angles (F) are equal
 lines||,s'ingcorrespond  ea
fb 
gc 
hd 

50. Parallel Line Theorems
a
b
c
d
e
f
h
g
Alternate angles (Z) are equal
 lines||,s'alternate  fc
ed 
Corresponding angles (F) are equal
 lines||,s'ingcorrespond  ea
fb 
gc 
hd 
Cointerior angles (C) are supplementary

51. Parallel Line Theorems
a
b
c
d
e
f
h
g
Alternate angles (Z) are equal
 lines||,s'alternate  fc
ed 
Corresponding angles (F) are equal
 lines||,s'ingcorrespond  ea
fb 
gc 
hd 
Cointerior angles (C) are supplementary
 lines||,180s'cointerior180  ec

52. Parallel Line Theorems
a
b
c
d
e
f
h
g
Alternate angles (Z) are equal
 lines||,s'alternate  fc
ed 
Corresponding angles (F) are equal
 lines||,s'ingcorrespond  ea
fb 
gc 
hd 
Cointerior angles (C) are supplementary
 lines||,180s'cointerior180  ec
180 fd

53. e.g. A B
C D
P
Q

x

y

65

120

54. e.g. A B
C D
P
Q

x

y

65

120
 
180straight18065  CQDx

55. e.g. A B
C D
P
Q

x

y

65

120
 
180straight18065  CQDx
115x

56. e.g. A B
C D
P
Q

x

y

65

120
 
180straight18065  CQDx
115x
Construct XY||CD passing through P
X Y

57. e.g. A B
C D
P
Q

x

y

65

120
 
180straight18065  CQDx
115x
Construct XY||CD passing through P
X Y
 QXYXPQ C||,s'alternate65  

58. e.g. A B
C D
P
Q

x

y

65

120
 
180straight18065  CQDx
115x
Construct XY||CD passing through P
X Y
 QXYXPQ C||,s'alternate65  
 XYABXPB ||,180s'cointerior180120 


59. e.g. A B
C D
P
Q

x

y

65

120
 
180straight18065  CQDx
115x
Construct XY||CD passing through P
X Y
 QXYXPQ C||,s'alternate65  
 XYABXPB ||,180s'cointerior180120 


60XPB

60. e.g. A B
C D
P
Q

x

y

65

120
 
180straight18065  CQDx
115x
Construct XY||CD passing through P
X Y
 QXYXPQ C||,s'alternate65  
 XYABXPB ||,180s'cointerior180120 


60XPB
  commonXPBXPQBPQ

61. e.g. A B
C D
P
Q

x

y

65

120
 
180straight18065  CQDx
115x
Construct XY||CD passing through P
X Y
 QXYXPQ C||,s'alternate65  
 XYABXPB ||,180s'cointerior180120 


60XPB
  commonXPBXPQBPQ
125
6065


y
y

62. e.g.
Book 2
Exercise 8A;
1cfh, 2bdeh,
3bd, 5bcf,
6bef, 10bd,
11b, 12bc,
13ad, 14, 15
A B
C D
P
Q

x

y

65

120
 
180straight18065  CQDx
115x
Construct XY||CD passing through P
X Y
 QXYXPQ C||,s'alternate65  
 XYABXPB ||,180s'cointerior180120 


60XPB
  commonXPBXPQBPQ
125
6065


y
y