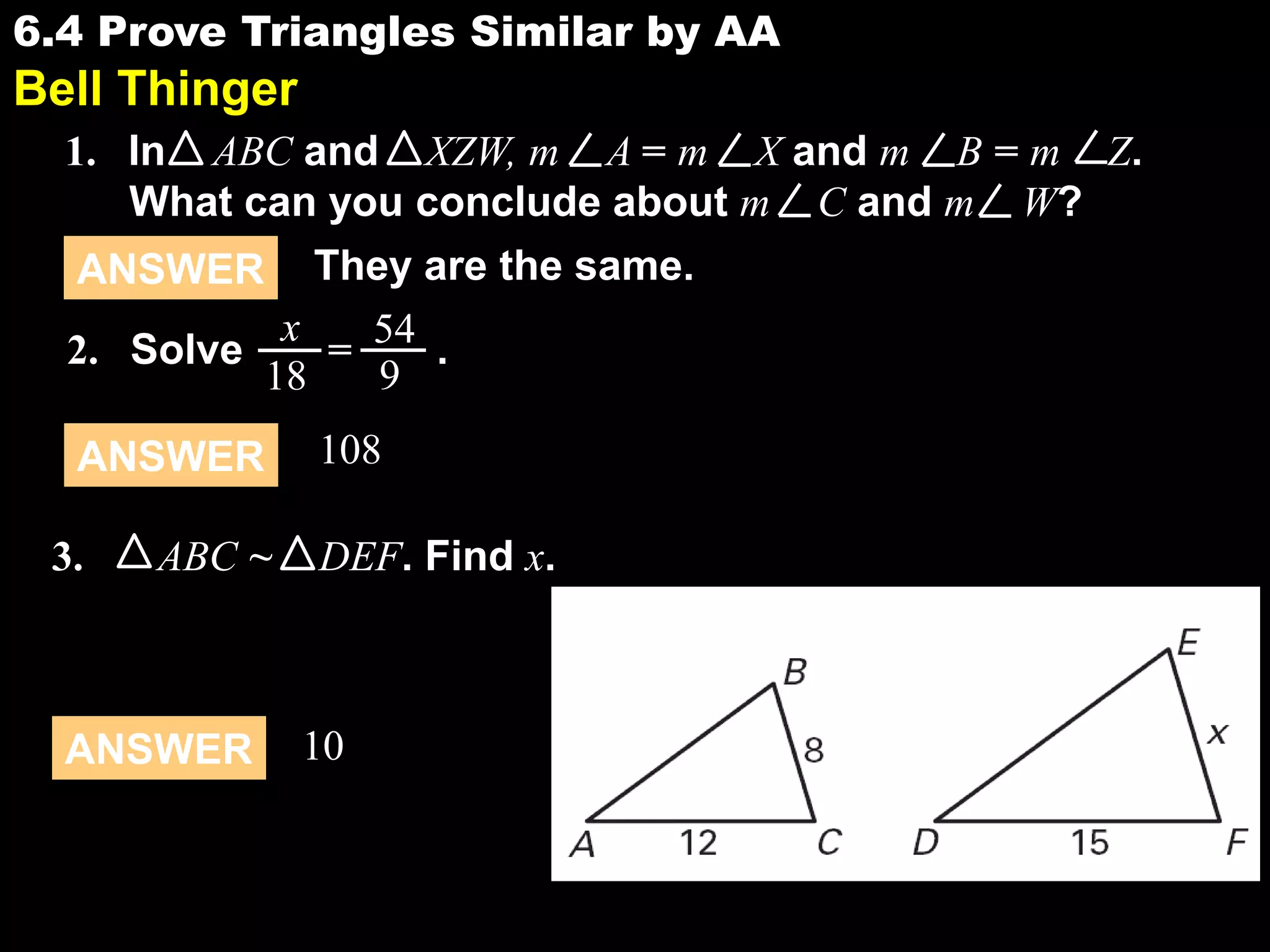
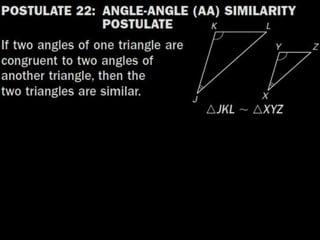
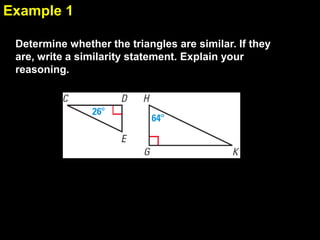
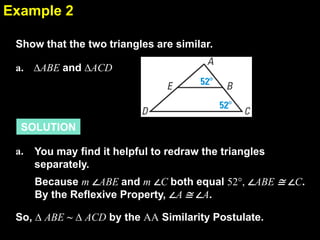
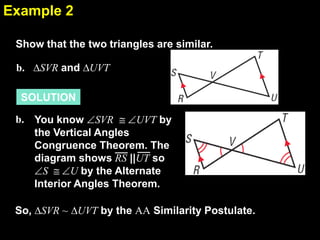
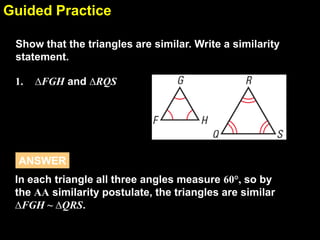
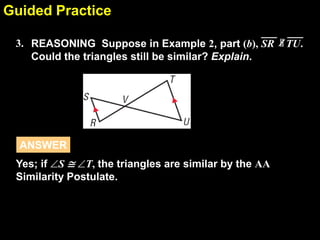
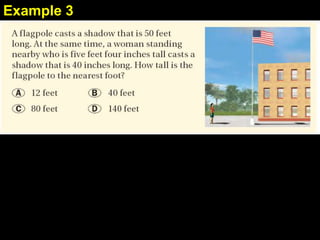
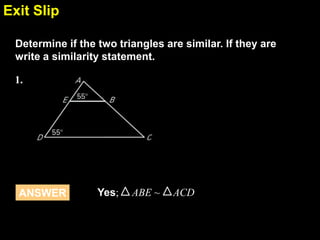
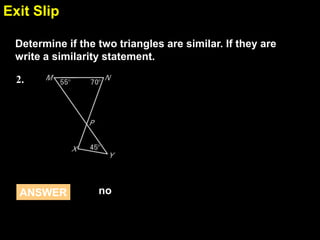
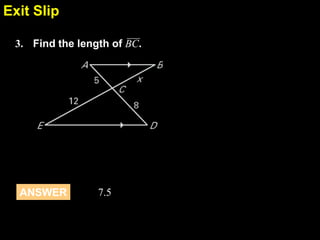
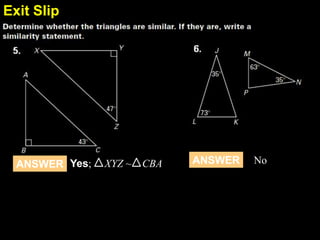
This document provides examples and explanations for proving triangles similar using the Angle-Angle (AA) criterion. It includes examples of showing two triangles are similar by showing they have two pairs of congruent angles. It also includes examples of writing similarity statements and using proportions to find missing side lengths when corresponding angles and one pair of corresponding sides are given. Guided practice problems allow students to practice determining if triangles are similar and writing similarity statements.

1. 6.4 Prove Triangles Similar by AA
6.4
Bell Thinger
1. In ABC and XZW, m A = m X and m B = m Z.
What can you conclude about m C and m W?
They are the same.
x
2. Solve
= 54 .
9
18
ANSWER
ANSWER
3.
ABC ~
ANSWER
108
DEF. Find x.
10

2. 6.4

3. Example 1
6.4
Determine whether the triangles are similar. If they
are, write a similarity statement. Explain your
reasoning.

4. Example 1
6.4
SOLUTION
Because they are both right angles, ∠D and ∠G are
congruent.
By the Triangle Sum Theorem, 26° + 90° + m ∠E =
180°, so m ∠E = 64°. Therefore, ∠E and ∠H are
congruent.
So, ∆CDE ~ ∆KGH by the AA Similarity Postulate.

5. Example 2
6.4
Show that the two triangles are similar.
a. ∆ABE and ∆ACD
SOLUTION
a.
You may find it helpful to redraw the triangles
separately.
Because m ∠ABE and m ∠C both equal 52°, ∠ABE ≅ ∠C.
By the Reflexive Property, ∠A ≅ ∠A.
So, ∆ ABE ~ ∆ ACD by the AA Similarity Postulate.

6. Example 2
6.4
Show that the two triangles are similar.
b. ∆SVR and ∆UVT
SOLUTION
b. You know SVR
UVT by
the Vertical Angles
Congruence Theorem. The
diagram shows RS ||UT so
S
U by the Alternate
Interior Angles Theorem.
So, ∆SVR ~ ∆UVT by the AA Similarity Postulate.

7. Guided Practice
6.4
Show that the triangles are similar. Write a similarity
statement.
1.
∆FGH and ∆RQS
ANSWER
In each triangle all three angles measure 60°, so by
the AA similarity postulate, the triangles are similar
∆FGH ~ ∆QRS.

8. Guided Practice
6.4
Show that the triangles are similar. Write a similarity
statement.
2.
∆CDF and ∆DEF
ANSWER
Since m CDF = 58° by the Triangle Sum Theorem
and m DFE = 90° by the Linear Pair Postulate the
two triangles are similar by the AA Similarity
Postulate; ∆CDF ~ ∆DEF.

9. Guided Practice
6.4
3. REASONING Suppose in Example 2, part (b), SR
Could the triangles still be similar? Explain.
ANSWER
Yes; if S ≅ T, the triangles are similar by the AA
Similarity Postulate.
TU.

10. Example 3
6.4

11. Example 3
6.4
SOLUTION
The flagpole and the woman form sides of two right
triangles with the ground, as shown below. The sun’s
rays hit the flagpole and the woman at the same
angle. You have two pairs of congruent angles, so the
triangles are similar by the AA Similarity Postulate.

12. Example 3
6.4
You can use a proportion to find the height x. Write 5
feet 4 inches as 64 inches so that you can form two
ratios of feet to inches.
x ft = 50 ft.
40 in.
64 in.
40x = 64(50)
x = 80
Write proportion of side lengths.
Cross Products Property
Solve for x.
ANSWER
The flagpole is 80 feet tall.
The correct answer is C.

13. Guided Practice
6.4
4. WHAT IF? A child who is 58 inches tall is standing
next to the woman that is 5’4” with a shadow 40”
long. How long is the child’s shadow?
ANSWER
36.25 in.

14. Guided Practice
6.4
5.
You are standing in your backyard, and you
measure the lengths of the shadows cast by both
you and a tree. Write a proportion showing how
you could find the height of the tree.
SAMPLE ANSWER
tree height
your height
=
length of shadow
length of your shadow

15. Exit Slip
6.4
Determine if the two triangles are similar. If they are
write a similarity statement.
1.
ANSWER
Yes;
ABE ~
ACD

16. Exit Slip
6.4
Determine if the two triangles are similar. If they are
write a similarity statement.
2.
ANSWER
no

17. Exit Slip
6.4
3. Find the length of BC.
ANSWER
7.5

18. Exit Slip
6.4
4.
A tree casts a shadow that is 30 feet long. At the
same time a person standing nearby, who is five
feet two inches tall, casts a shadow that is
50 inches long. How tall is the tree to the
nearest foot?
ANSWER
37 ft

19. Exit Slip
6.4
ANSWER Yes;
XYZ ~
CBA
ANSWER
No

20. 6.4
Homework
Pg 402-405
#9, 13, 16, 17, 32