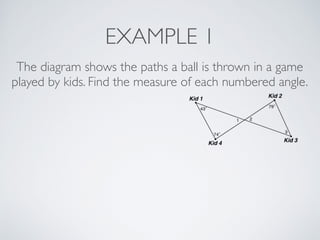
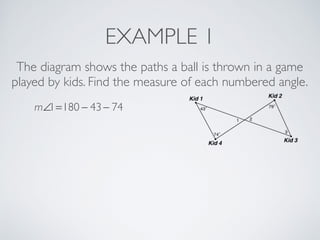
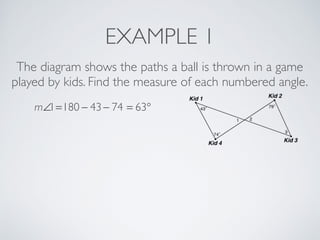
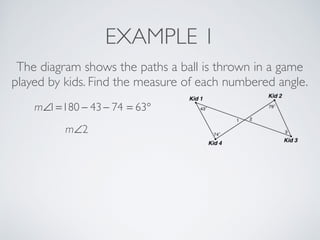
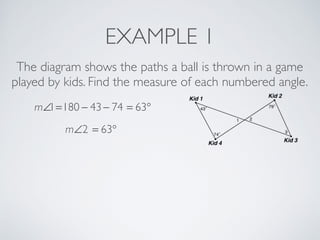
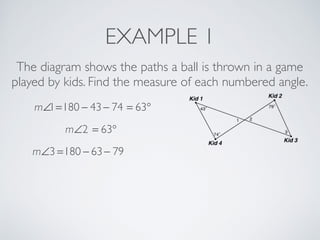
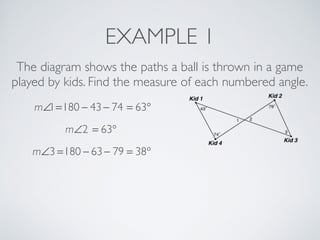
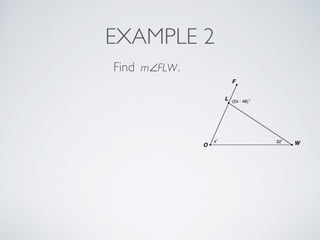
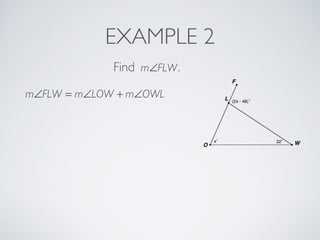
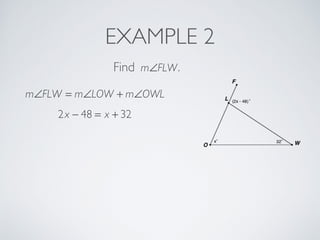
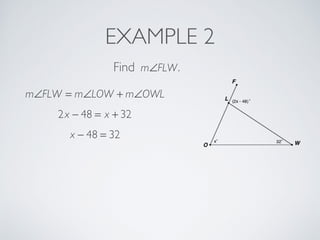
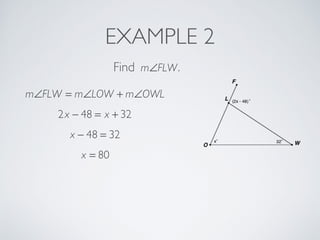
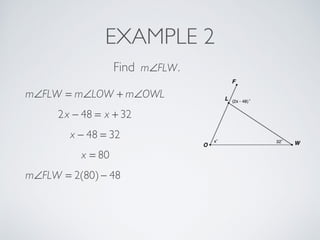
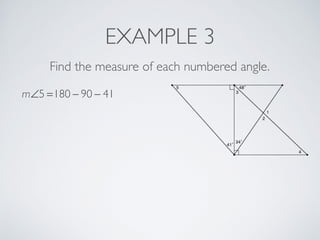
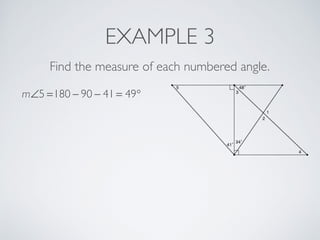
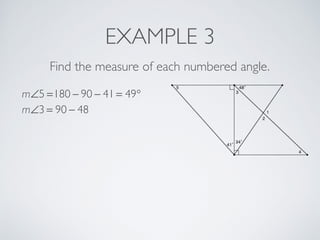
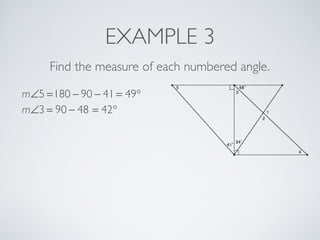
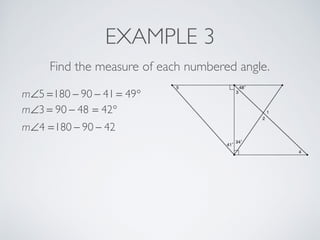
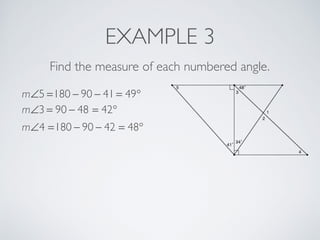
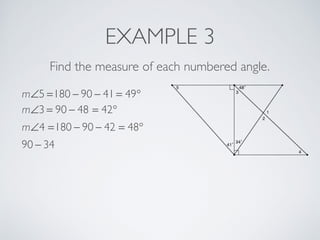
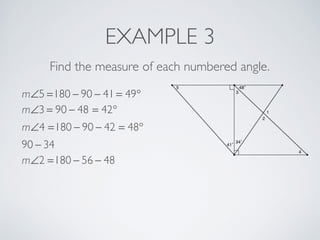
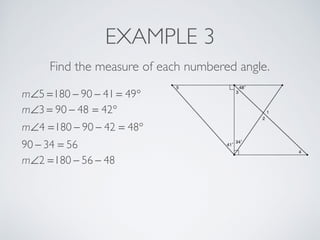
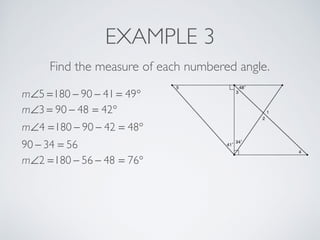
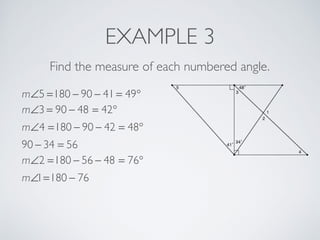
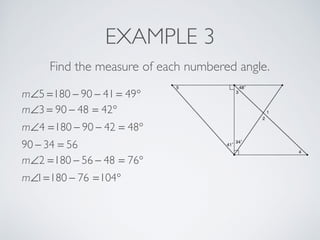
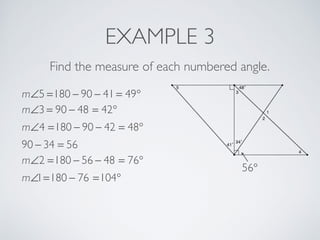
This document provides information about angles of triangles, including essential questions, vocabulary, theorems, examples, and a problem set. It defines key terms like auxiliary line, exterior angle, and remote interior angles. It presents the Triangle Angle-Sum Theorem stating the sum of interior angles is 180 degrees and the Exterior Angle Theorem relating exterior and remote interior angles. Examples demonstrate using these theorems to find angle measures. The final problem set directs working additional practice problems.

1. SECTION 4-2
Angles ofTriangles

2. ESSENTIAL QUESTIONS
• How do you apply theTriangle Angle-SumTheorem?
• How do you apply the Exterior AngleTheorem?

3. VOCABULARY
1.Auxiliary Line:
2. Exterior Angle:
3. Remote Interior Angles:
4. Flow Proof:

4. VOCABULARY
1.Auxiliary Line: An extra line or segment that is added to
a figure to help analyze geometric relationships
2. Exterior Angle:
3. Remote Interior Angles:
4. Flow Proof:

5. VOCABULARY
1.Auxiliary Line: An extra line or segment that is added to
a figure to help analyze geometric relationships
2. Exterior Angle: Formed outside a triangle when one side
of the triangle is extended;The exterior angle is adjacent
to the interior angle of the triangle
3. Remote Interior Angles:
4. Flow Proof:

6. VOCABULARY
1.Auxiliary Line: An extra line or segment that is added to
a figure to help analyze geometric relationships
2. Exterior Angle: Formed outside a triangle when one side
of the triangle is extended;The exterior angle is adjacent
to the interior angle of the triangle
3. Remote Interior Angles: The two interior angles that are
not adjacent to a given exterior angle
4. Flow Proof:

7. VOCABULARY
1.Auxiliary Line: An extra line or segment that is added to
a figure to help analyze geometric relationships
2. Exterior Angle: Formed outside a triangle when one side
of the triangle is extended;The exterior angle is adjacent
to the interior angle of the triangle
3. Remote Interior Angles: The two interior angles that are
not adjacent to a given exterior angle
4. Flow Proof: Uses statements written in boxes with
arrows to show a logical progression of an argument

8. THEOREMS & COROLLARIES
4.1 -Triangle Angle-SumTheorem:
4.2 - Exterior AngleTheorem:
4.1 Corollary:
4.2 Corollary:

9. THEOREMS & COROLLARIES
4.1 -Triangle Angle-SumTheorem: The sum of the
measures of the angles of any triangle is 180°
4.2 - Exterior AngleTheorem:
4.1 Corollary:
4.2 Corollary:

10. THEOREMS & COROLLARIES
4.1 -Triangle Angle-SumTheorem: The sum of the
measures of the angles of any triangle is 180°
4.2 - Exterior AngleTheorem: The measure of an exterior
angle of a triangle is equal to the sum of the measures of
the two remote interior angles
4.1 Corollary:
4.2 Corollary:

11. THEOREMS & COROLLARIES
4.1 -Triangle Angle-SumTheorem: The sum of the
measures of the angles of any triangle is 180°
4.2 - Exterior AngleTheorem: The measure of an exterior
angle of a triangle is equal to the sum of the measures of
the two remote interior angles
4.1 Corollary: The acute angles of a right triangle are
complementary
4.2 Corollary:

12. THEOREMS & COROLLARIES
4.1 -Triangle Angle-SumTheorem: The sum of the
measures of the angles of any triangle is 180°
4.2 - Exterior AngleTheorem: The measure of an exterior
angle of a triangle is equal to the sum of the measures of
the two remote interior angles
4.1 Corollary: The acute angles of a right triangle are
complementary
4.2 Corollary: There can be at most one right or obtuse
angle in a triangle

13. EXAMPLE 1
The diagram shows the paths a ball is thrown in a game
played by kids. Find the measure of each numbered angle.

14. EXAMPLE 1
The diagram shows the paths a ball is thrown in a game
played by kids. Find the measure of each numbered angle.
m∠1=180 − 43− 74

15. EXAMPLE 1
The diagram shows the paths a ball is thrown in a game
played by kids. Find the measure of each numbered angle.
m∠1=180 − 43− 74 = 63°

16. EXAMPLE 1
The diagram shows the paths a ball is thrown in a game
played by kids. Find the measure of each numbered angle.
m∠1=180 − 43− 74 = 63°
m∠2

17. EXAMPLE 1
The diagram shows the paths a ball is thrown in a game
played by kids. Find the measure of each numbered angle.
m∠1=180 − 43− 74 = 63°
m∠2 = 63°

18. EXAMPLE 1
The diagram shows the paths a ball is thrown in a game
played by kids. Find the measure of each numbered angle.
m∠1=180 − 43− 74 = 63°
m∠2 = 63°
m∠3 =180 − 63− 79

19. EXAMPLE 1
The diagram shows the paths a ball is thrown in a game
played by kids. Find the measure of each numbered angle.
m∠1=180 − 43− 74 = 63°
m∠2 = 63°
m∠3 =180 − 63− 79 = 38°

20. EXAMPLE 2
Find m∠FLW.

21. EXAMPLE 2
Find m∠FLW.
m∠FLW = m∠LOW + m∠OWL

22. EXAMPLE 2
Find m∠FLW.
m∠FLW = m∠LOW + m∠OWL
2x − 48 = x + 32

23. EXAMPLE 2
Find m∠FLW.
m∠FLW = m∠LOW + m∠OWL
2x − 48 = x + 32
x − 48 = 32

24. EXAMPLE 2
Find m∠FLW.
m∠FLW = m∠LOW + m∠OWL
2x − 48 = x + 32
x − 48 = 32
x = 80

25. EXAMPLE 2
Find m∠FLW.
m∠FLW = m∠LOW + m∠OWL
2x − 48 = x + 32
x − 48 = 32
x = 80
m∠FLW = 2(80)− 48

26. EXAMPLE 2
Find m∠FLW.
m∠FLW = m∠LOW + m∠OWL
2x − 48 = x + 32
x − 48 = 32
x = 80
m∠FLW = 2(80)− 48 =160 − 48

27. EXAMPLE 2
Find m∠FLW.
m∠FLW = m∠LOW + m∠OWL
2x − 48 = x + 32
x − 48 = 32
x = 80
m∠FLW = 2(80)− 48 =160 − 48 =112°

28. EXAMPLE 3
Find the measure of each numbered angle.

29. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41

30. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41 = 49°

31. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41 = 49°
m∠3 = 90 − 48

32. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41 = 49°
m∠3 = 90 − 48 = 42°

33. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41 = 49°
m∠3 = 90 − 48 = 42°
m∠4 =180 − 90 − 42

34. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41 = 49°
m∠3 = 90 − 48 = 42°
m∠4 =180 − 90 − 42 = 48°

35. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41 = 49°
m∠3 = 90 − 48 = 42°
m∠4 =180 − 90 − 42 = 48°
90 − 34

36. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41 = 49°
m∠3 = 90 − 48 = 42°
m∠4 =180 − 90 − 42 = 48°
90 − 34
m∠2 =180 − 56 − 48

37. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41 = 49°
m∠3 = 90 − 48 = 42°
m∠4 =180 − 90 − 42 = 48°
90 − 34 = 56
m∠2 =180 − 56 − 48

38. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41 = 49°
m∠3 = 90 − 48 = 42°
m∠4 =180 − 90 − 42 = 48°
90 − 34 = 56
m∠2 =180 − 56 − 48 = 76°

39. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41 = 49°
m∠3 = 90 − 48 = 42°
m∠4 =180 − 90 − 42 = 48°
90 − 34 = 56
m∠2 =180 − 56 − 48 = 76°
m∠1=180 − 76

40. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41 = 49°
m∠3 = 90 − 48 = 42°
m∠4 =180 − 90 − 42 = 48°
90 − 34 = 56
m∠2 =180 − 56 − 48 = 76°
m∠1=180 − 76 =104°

41. EXAMPLE 3
Find the measure of each numbered angle.
m∠5 =180 − 90 − 41 = 49°
m∠3 = 90 − 48 = 42°
m∠4 =180 − 90 − 42 = 48°
90 − 34 = 56
56°
m∠2 =180 − 56 − 48 = 76°
m∠1=180 − 76 =104°

42. PROBLEM SET

43. PROBLEM SET
p. 248 #1-37 odd, 46, 57
“We rarely think people have good sense unless they
agree with us.” - Francois de La Rochefoucauld