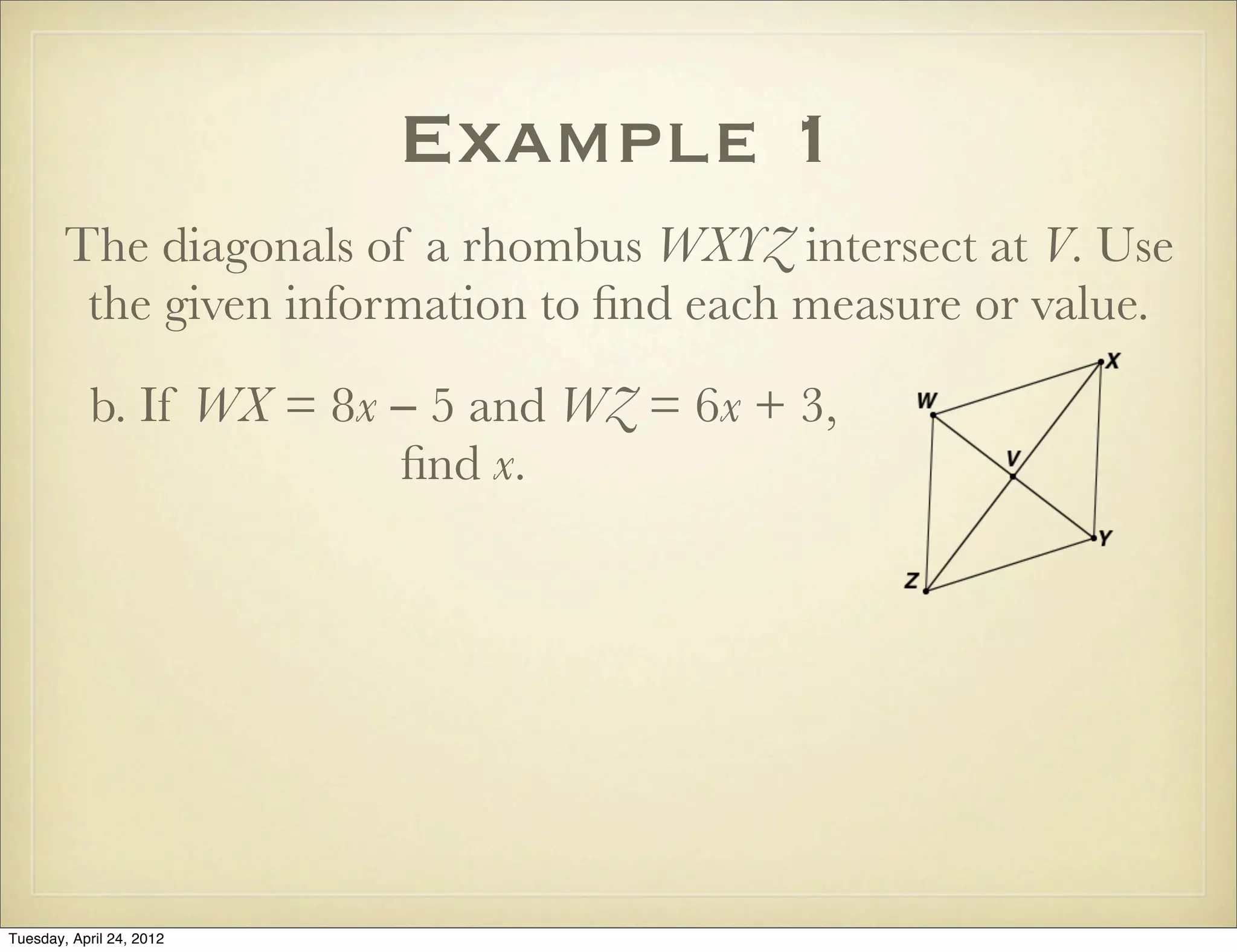
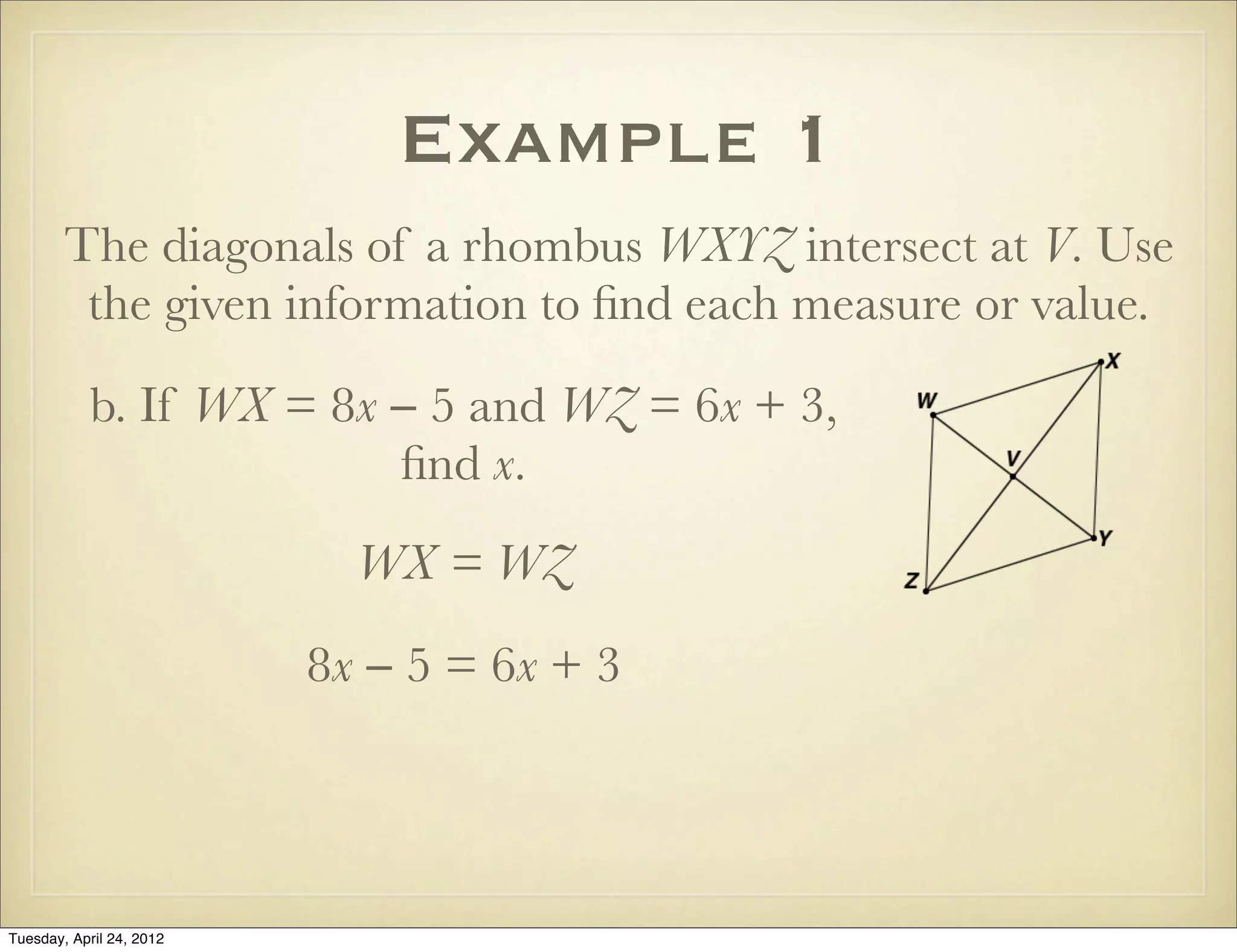
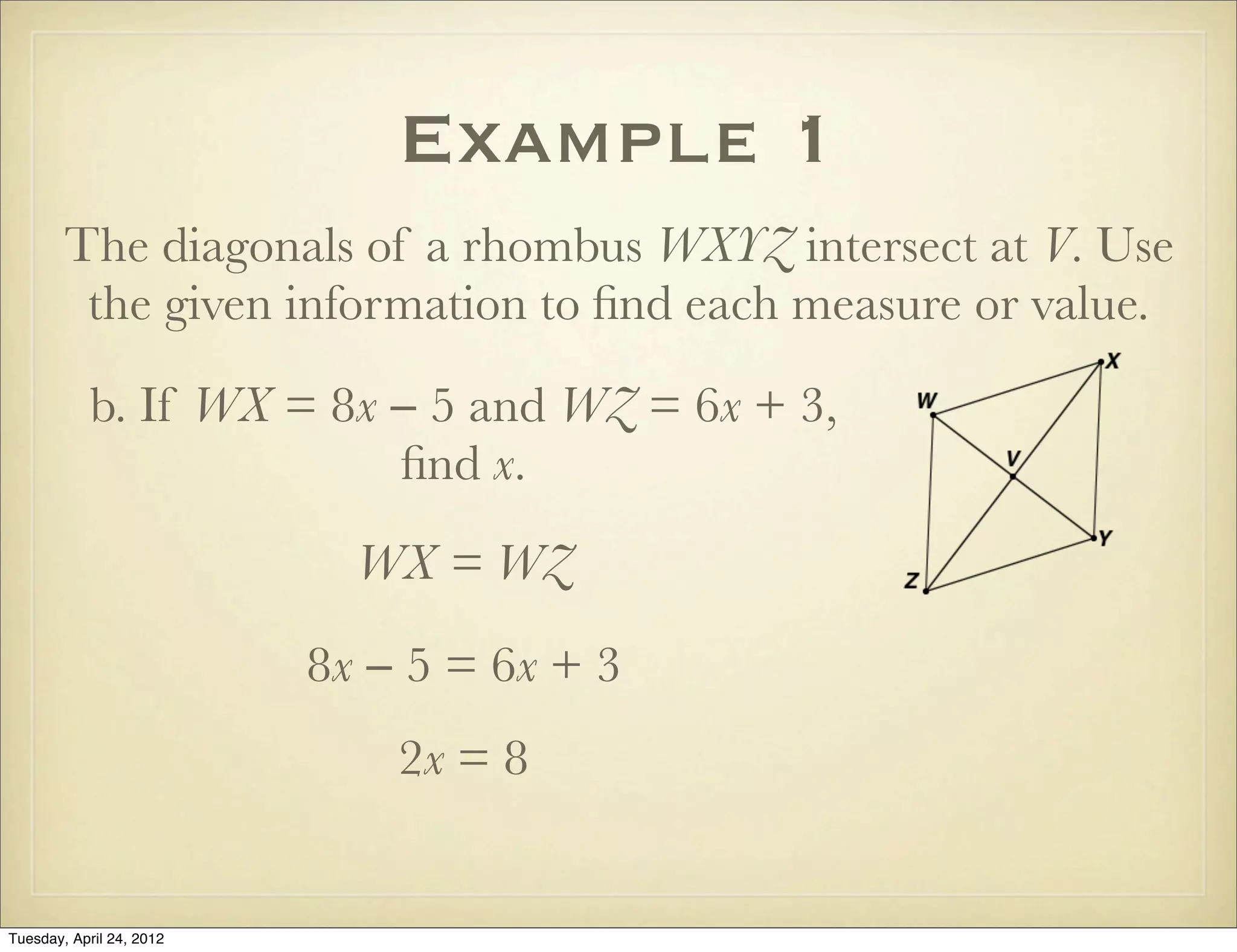
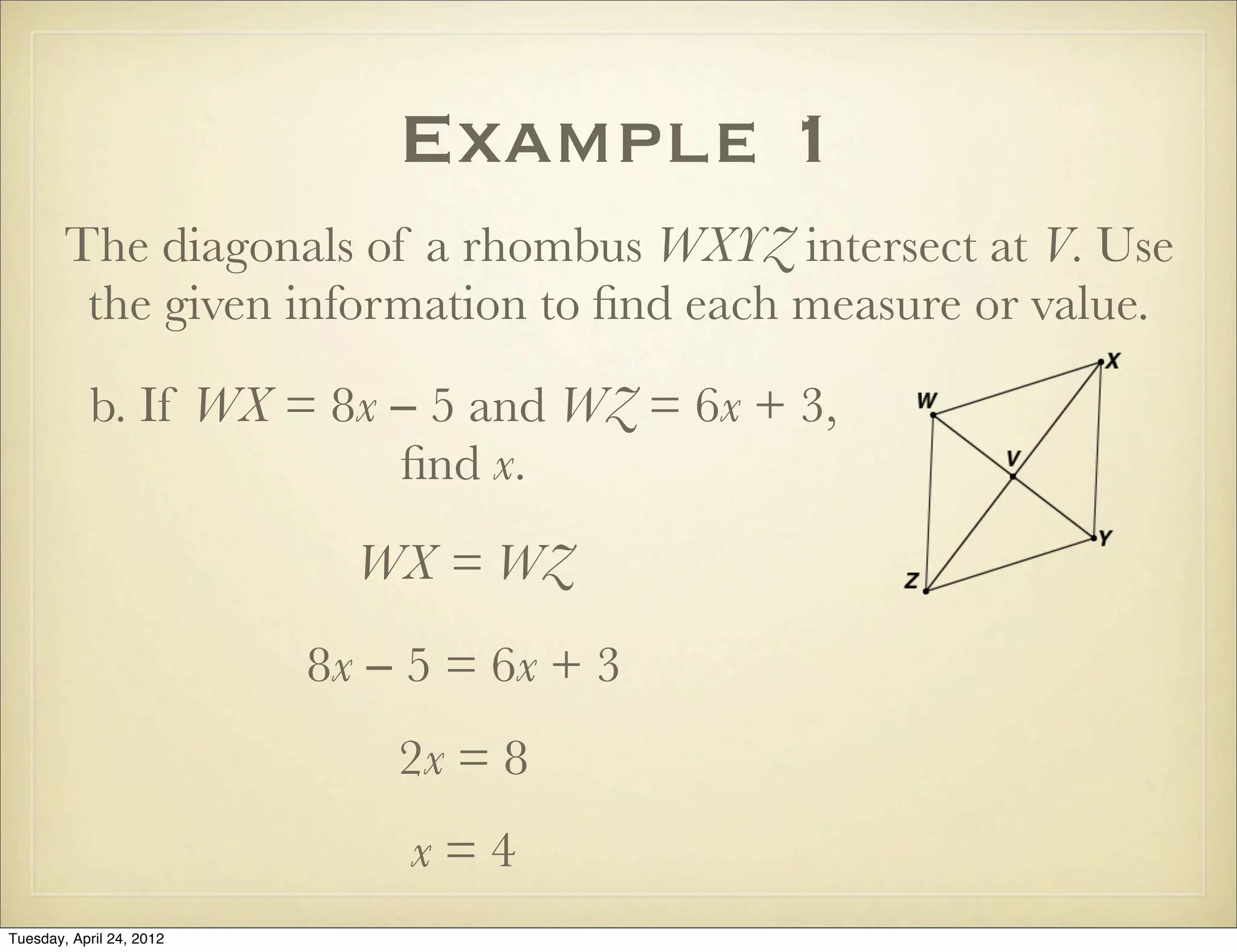
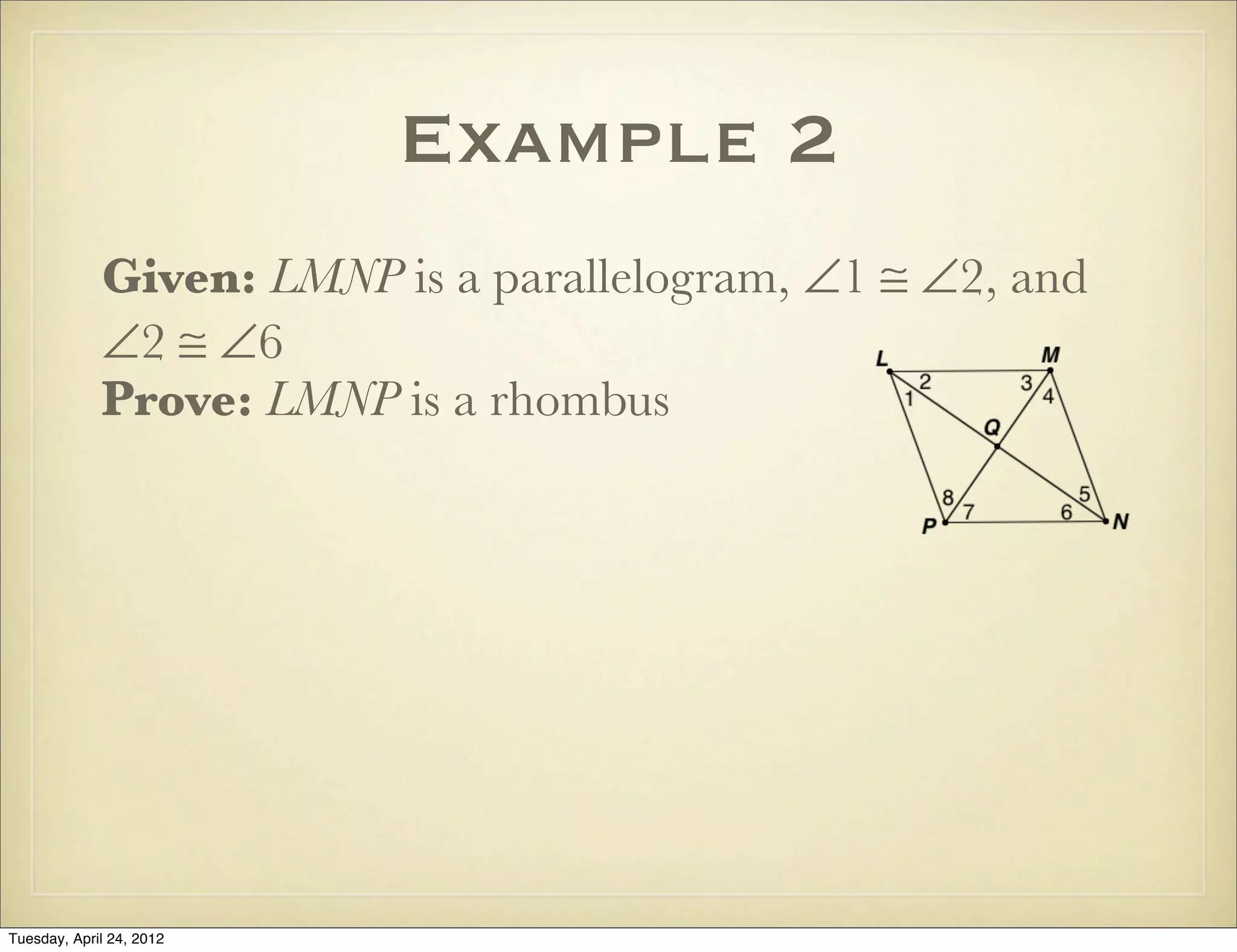
The document provides information about rhombi and squares including definitions, properties, theorems, examples, and a multi-step geometry problem. It defines a rhombus as a parallelogram with four congruent sides and lists its properties. It defines a square as a parallelogram with four right angles and lists common properties of squares, rectangles, and rhombi. Theorems are presented regarding diagonals of rhombi and conditions for rhombi and squares. Examples demonstrate using the properties and theorems to solve problems about classifying and determining measures of quadrilaterals.

1. Section 6-5
Rhombi and Squares
Tuesday, April 29, 14

2. Essential Questions
• How do you recognize and apply the properties of
rhombi and squares?
• How do you determine whether quadrilaterals are
rectangles, rhombi, or squares?
Tuesday, April 29, 14

3. Vocabulary
1. Rhombus:
Properties:
2. Square:
Properties:
Tuesday, April 29, 14

4. Vocabulary
1. Rhombus: A parallelogram with four congruent sides
Properties:
2. Square:
Properties:
Tuesday, April 29, 14

5. Vocabulary
1. Rhombus: A parallelogram with four congruent sides
Properties: All properties of parallelograms plus
four congruent sides, perpendicular diagonals, and
angles that are bisected by the diagonals
2. Square:
Properties:
Tuesday, April 29, 14

6. Vocabulary
1. Rhombus: A parallelogram with four congruent sides
Properties: All properties of parallelograms plus
four congruent sides, perpendicular diagonals, and
angles that are bisected by the diagonals
2. Square: A parallelogram with four congruent sides
and four right angles
Properties:
Tuesday, April 29, 14

7. Vocabulary
1. Rhombus: A parallelogram with four congruent sides
Properties: All properties of parallelograms plus
four congruent sides, perpendicular diagonals, and
angles that are bisected by the diagonals
2. Square: A parallelogram with four congruent sides
and four right angles
Properties: All properties of parallelograms,
rectangles, and rhombi
Tuesday, April 29, 14

8. Theorems
Diagonals of a Rhombus
6.15:
6.16:
Tuesday, April 29, 14

9. Theorems
Diagonals of a Rhombus
6.15: If a parallelogram is a rhombus, then its
diagonals are perpendicular
6.16:
Tuesday, April 29, 14

10. Theorems
Diagonals of a Rhombus
6.15: If a parallelogram is a rhombus, then its
diagonals are perpendicular
6.16: If a parallelogram is a rhombus, then each
diagonal bisects a pair of opposite angles
Tuesday, April 29, 14

11. Theorems
Conditions for Rhombi and Squares
6.17:
6.18:
6.19:
Tuesday, April 29, 14

12. Theorems
Conditions for Rhombi and Squares
6.17: If the diagonals of a parallelogram are
perpendicular, then the parallelogram is a rhombus
6.18:
6.19:
Tuesday, April 29, 14

13. Theorems
Conditions for Rhombi and Squares
6.17: If the diagonals of a parallelogram are
perpendicular, then the parallelogram is a rhombus
6.18: If one diagonal of a parallelogram bisects a
pair of opposite angles, then the parallelogram is a
rhombus
6.19:
Tuesday, April 29, 14

14. Theorems
Conditions for Rhombi and Squares
6.17: If the diagonals of a parallelogram are
perpendicular, then the parallelogram is a rhombus
6.18: If one diagonal of a parallelogram bisects a
pair of opposite angles, then the parallelogram is a
rhombus
6.19: If one pair of consecutive sides of a
parallelogram are congruent, then the parallelogram
is a rhombus
Tuesday, April 29, 14

15. Theorems
Conditions for Rhombi and Squares
6.20:
Tuesday, April 29, 14

16. Theorems
Conditions for Rhombi and Squares
6.20: If a quadrilateral is both a rectangle and a
rhombus, then it is a square
Tuesday, April 29, 14

17. Example 1
The diagonals of a rhombus WXYZ intersect at V. Use
the given information to find each measure or value.
a. If m∠WZX = 39.5°, find m∠ZYX.
Tuesday, April 29, 14

18. Example 1
The diagonals of a rhombus WXYZ intersect at V. Use
the given information to find each measure or value.
a. If m∠WZX = 39.5°, find m∠ZYX.
Since m∠WZX = 39.5°, we know that
m∠WZY = 79°.
Tuesday, April 29, 14

19. Example 1
The diagonals of a rhombus WXYZ intersect at V. Use
the given information to find each measure or value.
a. If m∠WZX = 39.5°, find m∠ZYX.
Since m∠WZX = 39.5°, we know that
m∠WZY = 79°.
180° − 79°
Tuesday, April 29, 14

20. Example 1
The diagonals of a rhombus WXYZ intersect at V. Use
the given information to find each measure or value.
a. If m∠WZX = 39.5°, find m∠ZYX.
Since m∠WZX = 39.5°, we know that
m∠WZY = 79°.
180° − 79° = 101°
Tuesday, April 29, 14

21. Example 1
The diagonals of a rhombus WXYZ intersect at V. Use
the given information to find each measure or value.
a. If m∠WZX = 39.5°, find m∠ZYX.
Since m∠WZX = 39.5°, we know that
m∠WZY = 79°.
180° − 79° = 101°
m∠ZYX = 101°
Tuesday, April 29, 14

22. Example 1
The diagonals of a rhombus WXYZ intersect at V. Use
the given information to find each measure or value.
b. If WX = 8x − 5 and WZ = 6x + 3,
find x.
Tuesday, April 29, 14

23. Example 1
The diagonals of a rhombus WXYZ intersect at V. Use
the given information to find each measure or value.
b. If WX = 8x − 5 and WZ = 6x + 3,
find x.
WX = WZ
Tuesday, April 29, 14

24. Example 1
The diagonals of a rhombus WXYZ intersect at V. Use
the given information to find each measure or value.
b. If WX = 8x − 5 and WZ = 6x + 3,
find x.
WX = WZ
8x − 5 = 6x + 3
Tuesday, April 29, 14

25. Example 1
The diagonals of a rhombus WXYZ intersect at V. Use
the given information to find each measure or value.
b. If WX = 8x − 5 and WZ = 6x + 3,
find x.
WX = WZ
8x − 5 = 6x + 3
2x = 8
Tuesday, April 29, 14

26. Example 1
The diagonals of a rhombus WXYZ intersect at V. Use
the given information to find each measure or value.
b. If WX = 8x − 5 and WZ = 6x + 3,
find x.
WX = WZ
8x − 5 = 6x + 3
2x = 8
x = 4
Tuesday, April 29, 14

27. Example 2
Given: LMNP is a parallelogram, ∠1 ≅ ∠2, and
∠2 ≅ ∠6
Prove: LMNP is a rhombus
Tuesday, April 29, 14

28. Example 2
Given: LMNP is a parallelogram, ∠1 ≅ ∠2, and
∠2 ≅ ∠6
Prove: LMNP is a rhombus
1. LMNP is a parallelogram,
∠1 ≅ ∠2, and ∠2 ≅ ∠6
Tuesday, April 29, 14

29. Example 2
Given: LMNP is a parallelogram, ∠1 ≅ ∠2, and
∠2 ≅ ∠6
Prove: LMNP is a rhombus
1. LMNP is a parallelogram,
∠1 ≅ ∠2, and ∠2 ≅ ∠6
1. Given
Tuesday, April 29, 14

30. Example 2
Given: LMNP is a parallelogram, ∠1 ≅ ∠2, and
∠2 ≅ ∠6
Prove: LMNP is a rhombus
1. LMNP is a parallelogram,
∠1 ≅ ∠2, and ∠2 ≅ ∠6
1. Given
2. LM ∣∣ PN and MN ∣∣ PL
Tuesday, April 29, 14

31. Example 2
Given: LMNP is a parallelogram, ∠1 ≅ ∠2, and
∠2 ≅ ∠6
Prove: LMNP is a rhombus
1. LMNP is a parallelogram,
∠1 ≅ ∠2, and ∠2 ≅ ∠6
1. Given
2. Def. of parallelogram2. LM ∣∣ PN and MN ∣∣ PL
Tuesday, April 29, 14

32. Example 2
Given: LMNP is a parallelogram, ∠1 ≅ ∠2, and
∠2 ≅ ∠6
Prove: LMNP is a rhombus
1. LMNP is a parallelogram,
∠1 ≅ ∠2, and ∠2 ≅ ∠6
1. Given
2. Def. of parallelogram
3. ∠5 ≅ ∠1
2. LM ∣∣ PN and MN ∣∣ PL
Tuesday, April 29, 14

33. Example 2
Given: LMNP is a parallelogram, ∠1 ≅ ∠2, and
∠2 ≅ ∠6
Prove: LMNP is a rhombus
1. LMNP is a parallelogram,
∠1 ≅ ∠2, and ∠2 ≅ ∠6
1. Given
2. Def. of parallelogram
3. ∠5 ≅ ∠1 3. Alt. int. ∠’s of ∣∣ lines ≅
2. LM ∣∣ PN and MN ∣∣ PL
Tuesday, April 29, 14

34. Example 2
Given: LMNP is a parallelogram, ∠1 ≅ ∠2, and
∠2 ≅ ∠6
Prove: LMNP is a rhombus
1. LMNP is a parallelogram,
∠1 ≅ ∠2, and ∠2 ≅ ∠6
1. Given
2. Def. of parallelogram
3. ∠5 ≅ ∠1 3. Alt. int. ∠’s of ∣∣ lines ≅
4. ∠1 ≅ ∠ 6 and ∠6 ≅ ∠5
2. LM ∣∣ PN and MN ∣∣ PL
Tuesday, April 29, 14

35. Example 2
Given: LMNP is a parallelogram, ∠1 ≅ ∠2, and
∠2 ≅ ∠6
Prove: LMNP is a rhombus
1. LMNP is a parallelogram,
∠1 ≅ ∠2, and ∠2 ≅ ∠6
1. Given
2. Def. of parallelogram
3. ∠5 ≅ ∠1 3. Alt. int. ∠’s of ∣∣ lines ≅
4. ∠1 ≅ ∠ 6 and ∠6 ≅ ∠5 4. Transitive
2. LM ∣∣ PN and MN ∣∣ PL
Tuesday, April 29, 14

36. Example 2
Given: LMNP is a parallelogram, ∠1 ≅ ∠2, and
∠2 ≅ ∠6
Prove: LMNP is a rhombus
1. LMNP is a parallelogram,
∠1 ≅ ∠2, and ∠2 ≅ ∠6
1. Given
2. Def. of parallelogram
3. ∠5 ≅ ∠1 3. Alt. int. ∠’s of ∣∣ lines ≅
4. ∠1 ≅ ∠ 6 and ∠6 ≅ ∠5 4. Transitive
5. LMNP is a rhombus
2. LM ∣∣ PN and MN ∣∣ PL
Tuesday, April 29, 14

37. Example 2
Given: LMNP is a parallelogram, ∠1 ≅ ∠2, and
∠2 ≅ ∠6
Prove: LMNP is a rhombus
1. LMNP is a parallelogram,
∠1 ≅ ∠2, and ∠2 ≅ ∠6
1. Given
2. Def. of parallelogram
3. ∠5 ≅ ∠1 3. Alt. int. ∠’s of ∣∣ lines ≅
4. ∠1 ≅ ∠ 6 and ∠6 ≅ ∠5 4. Transitive
5. LMNP is a rhombus 5. One diagonal bisects
opposite angles
2. LM ∣∣ PN and MN ∣∣ PL
Tuesday, April 29, 14

38. Example 3
Matt Mitarnowski is measuring the boundary of a
new garden. He wants the garden to be square. He
has set each of the corner stakes 6 feet apart.
What does Matt need to know to make sure that
the garden is a square?
Tuesday, April 29, 14

39. Example 3
Matt Mitarnowski is measuring the boundary of a
new garden. He wants the garden to be square. He
has set each of the corner stakes 6 feet apart.
What does Matt need to know to make sure that
the garden is a square?
Matt knows he at least has a rhombus as all four
sides are congruent. To make it a square, it must
also be a rectangle, so the diagonals must also be
congruent, as anything that is both a rhombus and
a rectangle is also a square.
Tuesday, April 29, 14

40. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
Tuesday, April 29, 14

41. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
Tuesday, April 29, 14

42. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
Tuesday, April 29, 14

43. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9
Tuesday, April 29, 14

44. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9 = 34
Tuesday, April 29, 14

45. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9 = 34
BD = (−1− 2)2
+ (3 + 2)2
Tuesday, April 29, 14

46. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9 = 34
BD = (−1− 2)2
+ (3 + 2)2
= (−3)2
+ (5)2
Tuesday, April 29, 14

47. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9 = 34
BD = (−1− 2)2
+ (3 + 2)2
= (−3)2
+ (5)2
= 9 + 25
Tuesday, April 29, 14

48. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9 = 34
BD = (−1− 2)2
+ (3 + 2)2
= (−3)2
+ (5)2
= 9 + 25 = 34
Tuesday, April 29, 14

49. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9 = 34
BD = (−1− 2)2
+ (3 + 2)2
= (−3)2
+ (5)2
= 9 + 25 = 34
The diagonals are congruent, so it is a rectangle
Tuesday, April 29, 14

50. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9 = 34
BD = (−1− 2)2
+ (3 + 2)2
= (−3)2
+ (5)2
= 9 + 25 = 34
The diagonals are congruent, so it is a rectangle
m( AC) =
2 +1
3 + 2
Tuesday, April 29, 14

51. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9 = 34
BD = (−1− 2)2
+ (3 + 2)2
= (−3)2
+ (5)2
= 9 + 25 = 34
The diagonals are congruent, so it is a rectangle
m( AC) =
2 +1
3 + 2
=
3
5
Tuesday, April 29, 14

52. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9 = 34
BD = (−1− 2)2
+ (3 + 2)2
= (−3)2
+ (5)2
= 9 + 25 = 34
The diagonals are congruent, so it is a rectangle
m( AC) =
2 +1
3 + 2
=
3
5
m(BD) =
−2 − 3
2 +1
Tuesday, April 29, 14

53. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9 = 34
BD = (−1− 2)2
+ (3 + 2)2
= (−3)2
+ (5)2
= 9 + 25 = 34
The diagonals are congruent, so it is a rectangle
m( AC) =
2 +1
3 + 2
=
3
5
m(BD) =
−2 − 3
2 +1
=
−5
3
Tuesday, April 29, 14

54. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9 = 34
BD = (−1− 2)2
+ (3 + 2)2
= (−3)2
+ (5)2
= 9 + 25 = 34
The diagonals are congruent, so it is a rectangle
m( AC) =
2 +1
3 + 2
=
3
5
m(BD) =
−2 − 3
2 +1
=
−5
3
AC ⊥ BD
Tuesday, April 29, 14

55. Example 4
Determine whether parallelogram ABCD is a
rhombus, rectangle, or square for A(−2, −1), B(−1, 3),
C(3, 2), and D(2, −2). List all that apply and
explain how you know.
AC = (−2 − 3)2
+ (−1− 2)2
= (−5)2
+ (−3)2
= 25 + 9 = 34
BD = (−1− 2)2
+ (3 + 2)2
= (−3)2
+ (5)2
= 9 + 25 = 34
The diagonals are congruent, so it is a rectangle
m( AC) =
2 +1
3 + 2
=
3
5
m(BD) =
−2 − 3
2 +1
=
−5
3
AC ⊥ BD
The diagonals are ⊥, so it is a rhombus, thus also a square.
Tuesday, April 29, 14

56. Problem Set
Tuesday, April 29, 14

57. Problem Set
p. 431 #1-33 odd, 46, 55, 57, 59
"Courage is saying, 'Maybe what I'm doing isn't
working; maybe I should try something else.'"
- Anna Lappe
Tuesday, April 29, 14