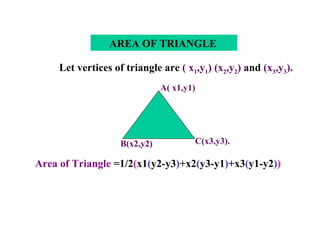
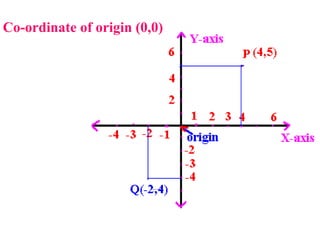
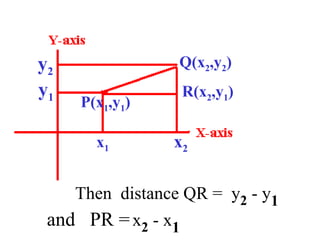
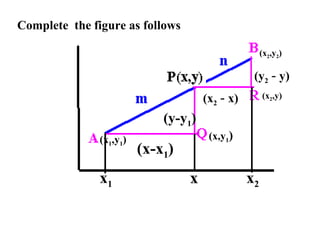
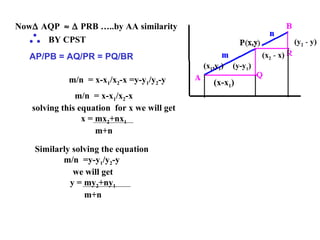
The document discusses coordinate geometry and defines key terms like axes of reference, coordinates of a point, distance formula, section formula, and area of a triangle. It provides examples of using these concepts and formulas to solve problems like finding the coordinates of a point dividing a line segment in a given ratio, or the area of a triangle given the coordinates of its vertices.






















![SOLUTION 1 Let co-ordinates of point R (X,Y) X = 4[2]+3[1] 4+3 X= {8+3]/7 = 11/7 Here m=4 , n=3, x 1 =1 , y 1 =2 x 2 = 2 , y 2 = 3 Y = 4[3]+3[2] 4+3 Y = [ 12+6]/7 = 18/7 Hence co-ordinates of R = (11/7 , 18/7)](https://image.slidesharecdn.com/coordinategeometry11-100105105748-phpapp01/85/Coordinategeometry1-1-29-320.jpg)