- Fuzzy logic was developed by Lotfi Zadeh to address applications involving subjective or vague data like "attractive person" that cannot be easily analyzed using binary logic. It allows for partial truth values between completely true and completely false. - Fuzzy logic controllers mimic human decision making and involve fuzzifying inputs, applying fuzzy rules, and defuzzifying outputs. This allows systems to be specified in human terms and automated. 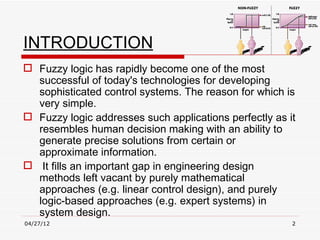- Fuzzy logic has many applications from industrial process control to consumer products like washing machines and microwaves. It offers an intuitive way to model real-world ambiguities compared to mathematical or logic-based approaches.

1. -PRIYA
SRIVASTAVA
04/27/12 090105801 1

2. INTRODUCTION
 Fuzzy logic has rapidly become one of the most
successful of today's technologies for developing
sophisticated control systems. The reason for which is
very simple.
 Fuzzy logic addresses such applications perfectly as it
resembles human decision making with an ability to
generate precise solutions from certain or
approximate information.
 It fills an important gap in engineering design
methods left vacant by purely mathematical
approaches (e.g. linear control design), and purely
logic-based approaches (e.g. expert systems) in
system design.
04/27/12 2

3.  While other approaches require accurate equations to
model real-world behaviors, fuzzy design can
accommodate the ambiguities of real-world human
language and logic.
 It provides both an intuitive method for describing
systems in human terms and automates the
conversion of those system specifications into
effective models.
04/27/12 3

4. CHRONICLE:-
 Lotfi A. Zadeh, a professor of UC Berkeley in
California, soon to be known as the founder of fuzzy
logic observed that conventional computer logic was
incapable of manipulating data representing subjective
or vague human ideas such as "an atractive person" .
 Fuzzy logic, hence was designed to allow computers
to determine the distinctions among data with shades
of gray, similar to the process of human reasoning.
 This theory proposed making the membership
function (or the values False and True) operate over
the range of real numbers [0.0, 1.0]. Fuzzy logic was
now introduced to the world.
04/27/12 4

5. t d o yo u m e a n b y f u z z y
 Fuzzy logic is a superset of Boolean logic that has
been extended to handle the concept of partial truth-
truth values between "completely true" and
"completely false".
The essential characteristics of fuzzy logicare as
follows:-
 In fuzzy logic, exact reasoning is viewed as a limiting
case of approximate reasoning.
 In fuzzy logic everything is a matter of degree.
 Any logical system can be fuzzified
 In fuzzy logic, knowledge is interpreted as a collection
of elastic or, equivalently , fuzzy constraint on a
collection of variables
 The third statement hence, define Boolean logic as a
subset of Fuzzy logic.
04/27/12 5

6. F uzzy S e ts
 A paradigm is a set of rules and regulations which
defines boundaries and tells us what to do to be
successful in solving problems within these
boundaries.
 For example the use of transistors instead of vacuum
tubes is a paradigm shift - likewise the development of
Fuzzy Set Theory from conventional bivalent set
theory is a paradigm shift.
 Bivalent Set Theory can be somewhat limiting if we
wish to describe a 'humanistic' problem
mathematically.
04/27/12 6

7. Fig. below illustrates bivalent sets to
characterise the temperature of a room.
04/27/12 7

8. F u z z y S e t O p e r a t io n s .
 U n io n
 The membership function of the Union of two fuzzy sets A
and B with membership functions and respectively is
defined as the maximum of the two individual membership
functions. This is called the maximum criterion.
04/27/12 8

9. W h a t d o e s it o f f e r ?
 The first applications of fuzzy theory were primarily
industrial, such as process control for cement kilns.
 Since then, the applications of Fuzzy Logic technology
have virtually exploded, affecting things we use
everyday.
Take for example, the fuzzy washing machine .
 A load of clothes in it and press start, and the
machine begins to churn, automatically choosing the
best cycle. The fuzzy microwave, Place chili,
potatoes, or etc in a fuzzy microwave and push single
button, and it cooks for the right time at the proper
temperature.
 The fuzzy car, maneuvers itself by following simple
verbal instructions from its driver. It can even stop
itself when there is an obstacle immediately ahead 9
04/27/12
using sensors.

10. H o w d o f u z z y s e t s d if f e r
f r o m c la s s ic a l s e t s ?
 In classical set theory we assume that all sets rare
well-defined (or crisp), that is given any object in our
universe we can always say that object either is or is
not the member of a particular set.
 CLASSICAL SETS
 The set of people that can run a mile in 4 minutes or
less.
 The set of children under age seven that weigh more
than 1oo pounds.
 FUZZY SETS
 The set of fast runners.
 The set of overweight children.
04/27/12 10

11. E Q U A L IT Y O F F U Z Z Y S E T S :-
 Let A={ Mohan/.2;Sohan/1;John/7;Abrahm/4}
 B= {Abrahm/4;Mohan/.2;John/7;Sohan/1}
 However, if
 C={Abrahm/2;Mohan/.4;Sohan/1;John}
 A = B and A ≠ C
04/27/12 11

12. F U Z Z Y C O N TR O L :-
 Fuzzy control, which directly uses fuzzy rules is the
most important application in fuzzy theory.
 Using a procedure originated by Ebrahim Mamdani in
the late 70s, three steps are taken to create a fuzzy
controlled machine:
 1)Fuzzification(Using membership functions to
graphically describe a situation)

2)Rule evaluation(Application of fuzzy rules)

3)Defuzzification(Obtaining the crisp or actual results)
04/27/12 12

13. WH Y F U Z Z Y C O N TR O L ?
 Fuzzy Logic is a technique to embody human like
thinking into a control system.
 A fuzzy controller is designed to emulate human
deductive thinking, that is, the process people use to
infer conclusions from what they know.
 Traditional control approach requires formal modeling
of the physical reality.
04/27/12 13

14.  A f u z z y c o n t r o l s y s t e m can also be
described as based on fuzzy logic—a mathematical
system that analyzes analog input values in terms of
logical variables that take on continuous values
between 0 and 1, in contrast to classical or digital
logic, which operates on discrete values of either 1 or
0 (true or false respectively).
04/27/12 14

15.  Fuzzy logic is widely used in machine control.
 The term itself inspires a certain skepticism, sounding
equivalent to "half-baked logic" or "bogus logic", but
the "fuzzy" part does not refer to a lack of rigour in the
method, rather to the fact that the logic involved can
deal with fuzzy concepts—concepts that cannot be
expressed as "true" or "false" but rather as "partially
true".
04/27/12 15

16.  Although genetic algorithms and neural networks can
perform just as well as fuzzy logic in many cases,
 fuzzy logic has the advantage that the solution to the
problem can be cast in terms that human operators
can understand,
 so that their experience can be used in the design of
the controller. This makes it easier to mechanize tasks
that are already successfully performed by humans.
04/27/12 16

17. L IT T L E M O R E O N F U Z Z Y
C O N T R O L :-
 Fuzzy controllers are very simple conceptually.
They consist of an input stage, a processing
stage, and an output stage.
 The input stage maps sensor or other inputs,
such as switches, thumbwheels, and so on, to the
appropriate membership functions and truth
values.
 The processing stage invokes each appropriate
rule and generates a result for each, then
combines the results of the rules. Finally, the
output stage converts the combined result back
into a specific control output value.
04/27/12 17

18. H o w f a r c a n f u z z y lo g ic
go???
 It can appear almost anyplace where computers and
modern control theory are overly precise as well as in
tasks requiring delicate human intuition and
experience-based knowledge. What does the future
hold?
 Computers that understand and respond to normal
human language.
Machines that write interesting novels and
screenplays in a selected style , such as
Hemingway's.
 Molecule-sized soldiers of health that will roam the
blood-stream, killing cancer cells and slowing the
04/27/12 18
aging process.

19.  Hence, it can be seen that with the enormous
research currently being done in Japan and many
other countries whose eyes have opened, the future
of fuzzy logic is undetermined. There is no limit to
where it can go.
The future is bright. The future is fuzzy.
04/27/12 19

20. 04/27/12 20