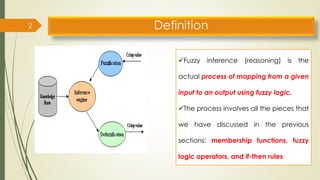
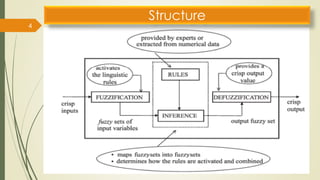
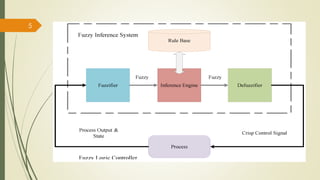
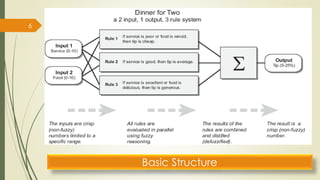
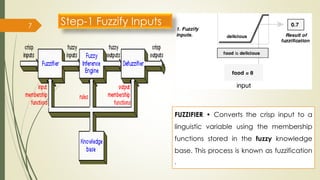
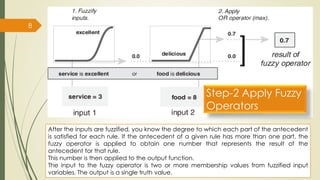
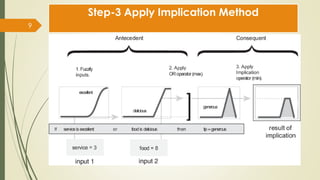
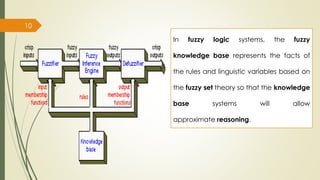
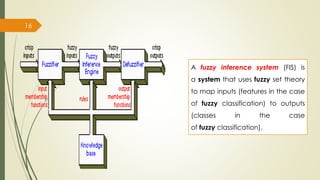
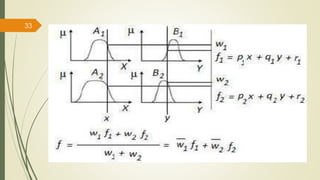
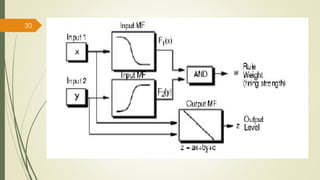
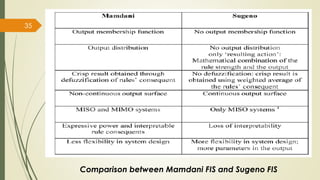
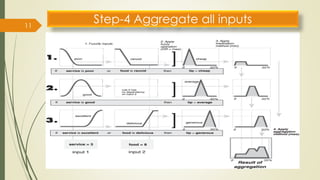
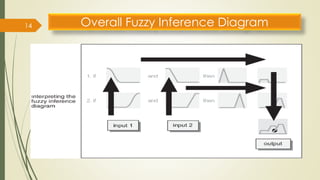
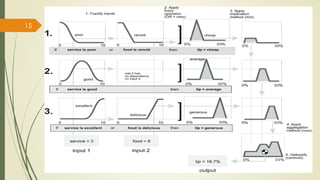
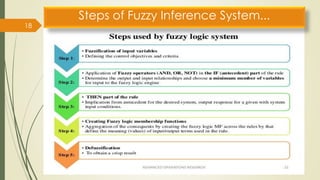
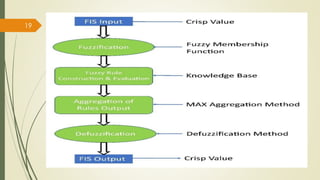
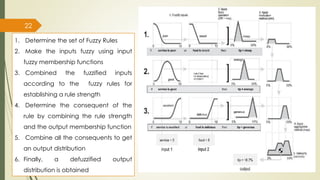
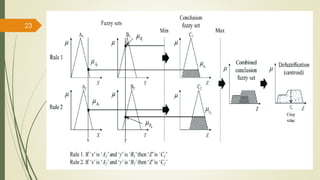
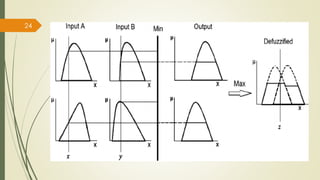
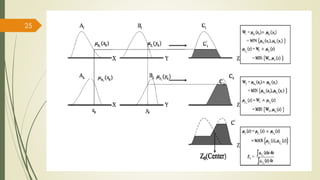
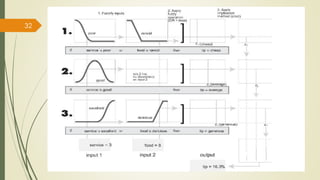
Fuzzy inference systems use fuzzy logic to map inputs to outputs. There are two main types: Mamdani systems use fuzzy outputs and are well-suited for problems involving human expert knowledge. Sugeno systems have faster computation using linear or constant outputs. The fuzzy inference process involves fuzzifying inputs, applying fuzzy logic operators, and using if-then rules. Outputs are determined through implication, aggregation, and defuzzification. Mamdani systems find the centroid of fuzzy outputs while Sugeno uses weighted averages, making it more efficient.

1. Fuzzy Inference Systems
Course: Computational Intelligence Engineering (Soft Computing)
Prof. (Dr.) Pravat Kumar Rout
Department of EEE, ITER,
Siksha ‘O’Anusandhan (Deemed to be University),
Bhubaneswar, Odisha, India
1

2. Definition
2
✓Fuzzy inference (reasoning) is the
actual process of mapping from a given
input to an output using fuzzy logic.
✓The process involves all the pieces that
we have discussed in the previous
sections: membership functions, fuzzy
logic operators, and if-then rules

3. Fuzzy Inference System
 Fuzzy inference is a method that interprets the values in the input vector and, based
on some sets of rules, assigns values to the output vector. In fuzzy logic, the truth of
any statement becomes a matter of a degree.
 Fuzzy inference is the process of formulating the mapping from a given input to an
output using fuzzy logic. The mapping then provides a basis from which decisions
can be made or patterns discerned.
 The process of fuzzy inference involves all of the pieces described so far, i.e.,
membership functions, fuzzy logic operators, and if-then rules.
 Two main types of fuzzy inference systems can be implemented: Mamdani-type
(1977) and Sugeno-type (1985). These two types of inference systems vary
somewhat in the way outputs are determined.
3

4. 4
Structure

5. 5

6. 6
Basic Structure

7. 7
FUZZIFIER • Converts the crisp input to a
linguistic variable using the membership
functions stored in the fuzzy knowledge
base. This process is known as fuzzification
.
Step-1 Fuzzify Inputs

8. 8
After the inputs are fuzzified, you know the degree to which each part of the antecedent
is satisfied for each rule. If the antecedent of a given rule has more than one part, the
fuzzy operator is applied to obtain one number that represents the result of the
antecedent for that rule.
This number is then applied to the output function.
The input to the fuzzy operator is two or more membership values from fuzzified input
variables. The output is a single truth value.
Step-2 Apply Fuzzy
Operators

9. 9
Step-3 Apply Implication Method

10. 10
In fuzzy logic systems, the fuzzy
knowledge base represents the facts of
the rules and linguistic variables based on
the fuzzy set theory so that the knowledge
base systems will allow
approximate reasoning.

11. 11
Step-4 Aggregate all inputs

12. 12
Step-5 Defuzzify

13. 13
•Defuzzification is the process of producing
a quantifiable result in Crisp logic, given
fuzzy sets and corresponding membership
degrees.
•It is the process that maps a fuzzy set to a
crisp set.
•It is typically needed in fuzzy
control systems. These will have a number
of rules that transform a number of
variables into a fuzzy result, that is, the
result is described in terms of membership
in fuzzy sets .
•For example, rules designed to decide
how much pressure to apply might result in
"Decrease Pressure (15%), Maintain
Pressure (34%), Increase Pressure (72%)".
Defuzzification is interpreting the
membership degrees of the fuzzy sets into
a specific decision or real value.

14. 14 Overall Fuzzy Inference Diagram

15. 15

16. 16
A fuzzy inference system (FIS) is
a system that uses fuzzy set theory
to map inputs (features in the case
of fuzzy classification) to outputs
(classes in the case
of fuzzy classification).

17. Steps of Fuzzy Inference System
The steps of fuzzy reasoning (inference operations upon fuzzy IF–THEN rules)
performed by FISs are:
 1.Compare the input variables with the membership functions on the
antecedent part to obtain the membership values of each linguistic label. (this
step is often called fuzzification.)
 2. Combine (usually multiplication or min) the membership values on the
premise part to get firing strength (deree of fullfillment) of each rule.
 3. Generate the qualified consequents (either fuzzy or crisp) or each rule
depending on the firing strength.
 4. Aggregate the qualified consequents to produce a crisp output. (This step is
called defuzzification.)
17

18. 18
Steps of Fuzzy Inference System...

19. 19

20. Mamdani-type inference
 Mamdani-type inference expects the output membership functions to be fuzzy sets.
 After the aggregation process, there is a fuzzy set for each output variable, which
needs defuzzification.
 It is possible, and sometimes more efficient, to use a single spike as the output
membership function rather than a distributed fuzzy set.
 This, sometimes called a singleton output membership function, can be considered
a pre-defuzzified fuzzy set.
 It enhances the efficiency of the defuzzification process because it greatly simplifies
the computation required by the more general Mamdani method, which finds the
centroid of a two-dimensional function. Instead of integrating across the two-
dimensional function to find the centroid, the weighted average of a few data
points can be used.
20

21. Mamdani Fuzzy Inference Systems
 Mamdani fuzzy inference was first introduced as a method to create a control
system by synthesizing a set of linguistic control rules obtained from experienced
human operators. In a Mamdani system, the output of each rule is a fuzzy set.
 Since Mamdani systems have more intuitive and easier to understand rule bases,
they are well-suited to expert system applications where the rules are created from
human expert knowledge, such as medical diagnostics.
 The output of each rule is a fuzzy set derived from the output membership function
and the implication method of the FIS. These output fuzzy sets are combined into a
single fuzzy set using the aggregation method of the FIS. Then, to compute a final
crisp output value, the combined output fuzzy set is defuzzified using one of the
methods described in Defuzzification Methods .
21

22. 22
1. Determine the set of Fuzzy Rules
2. Make the inputs fuzzy using input
fuzzy membership functions
3. Combined the fuzzified inputs
according to the fuzzy rules for
establishing a rule strength
4. Determine the consequent of the
rule by combining the rule strength
and the output membership function
5. Combine all the consequents to get
an output distribution
6. Finally, a defuzzified output
distribution is obtained

23. 23

24. 24

25. 25

26. Mamdani Fuzzy Inference System
 Intuitive
 Well-suited to human input
 More interpretable rule base
 Have widespread acceptance
26

27. Sugeno method of fuzzy inference
 The Sugeno method of fuzzy inference is similar to the Mamdani method in
many respects.
 The first two parts of the fuzzy inference process, fuzzifying the inputs and
applying the fuzzy operator, are exactly the same.
 The main difference between Mamdani-type and Sugeno-type fuzzy
inference is that the output membership functions are only linear or constant
for the Sugeno-type fuzzy inference.
 A typical fuzzy rule in a first-order Sugeno fuzzy model has the form. where A
and B are fuzzy sets in the antecedent, while p, q, and r are all constants.
27

28. Continue...
 Higher-order Sugeno fuzzy models are possible, but they introduce significant
complexity with little obvious merit.
 Because of the linear dependence of each rule on the system’s input
variables, the Sugeno method is ideal for acting as an interpolating supervisor
of multiple linear controllers that are to be applied, respectively, to different
operating conditions of a dynamic nonlinear systems.
 A Sugeno fuzzy inference system is extremely well suited to the task of
smoothly interpolating the linear gains that would be applied across the input
space, i.e., it is a natural and efficient gain scheduler.
 Similarly, a Sugeno system is suitable for modeling nonlinear systems by
interpolating multiple linear models.
28

29. Sugeno Fuzzy Inference System
 Sugeno fuzzy inference, also referred to as Takagi-Sugeno-Kang fuzzy inference,
uses singleton output membership functions that are either constant or a linear
function of the input values.
 The defuzzification process for a Sugeno system is more computationally efficient
compared to that of a Mamdani system, since it uses a weighted average or
weighted sum of a few data points rather than compute a centroid of a two-
dimensional area.
29

30. 30

31. 31

32. 32

33. 33

34. Sugeno Fuzzy Inference System
 Computationally efficient
 Work well with linear techniques, such as PID control
 Work well with optimization and adaptive techniques
 Guarantee output surface continuity
 Well-suited to mathematical analysis
34

35. 35
Comparison between Mamdani FIS and Sugeno FIS

36. 36