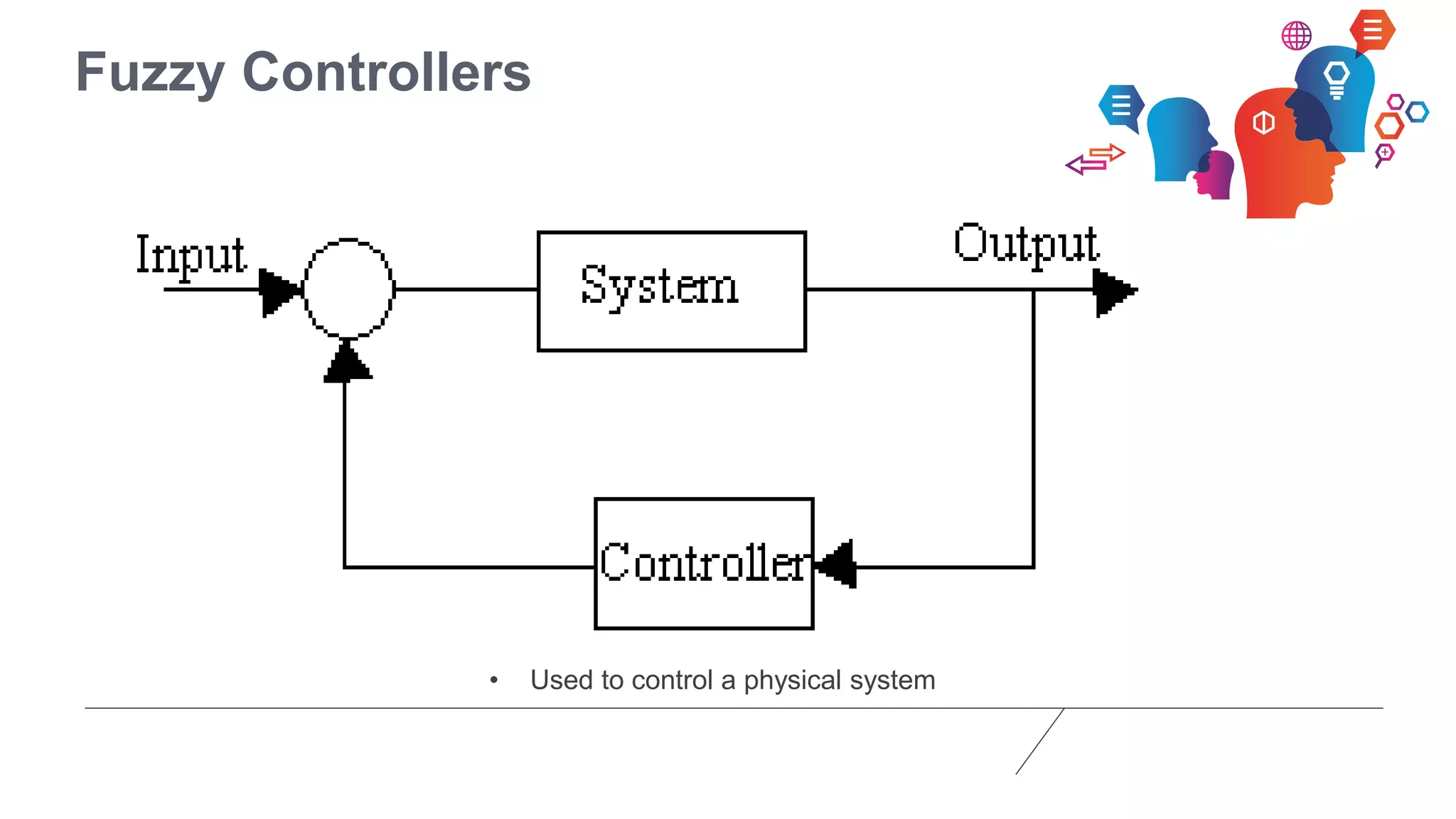
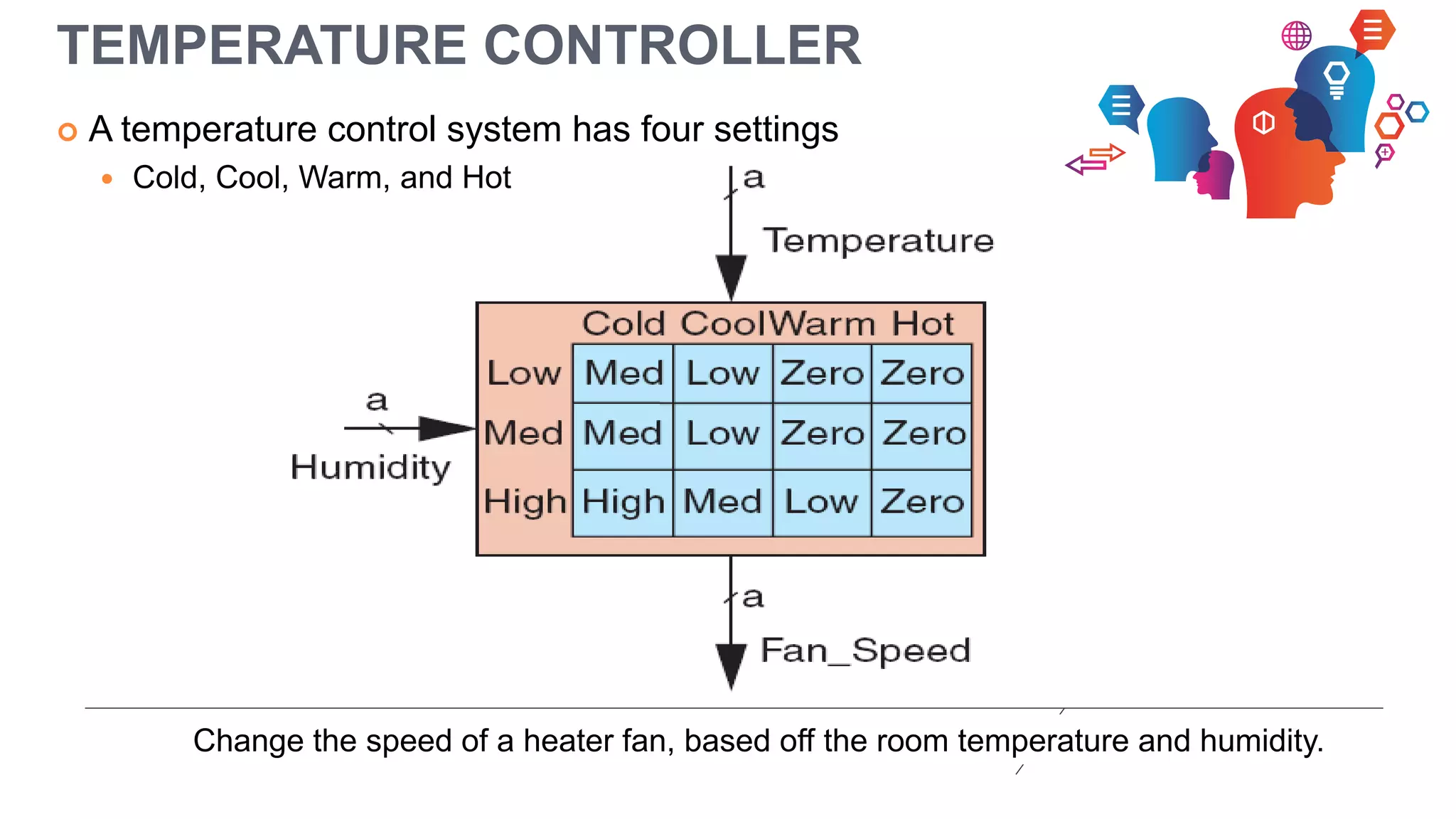
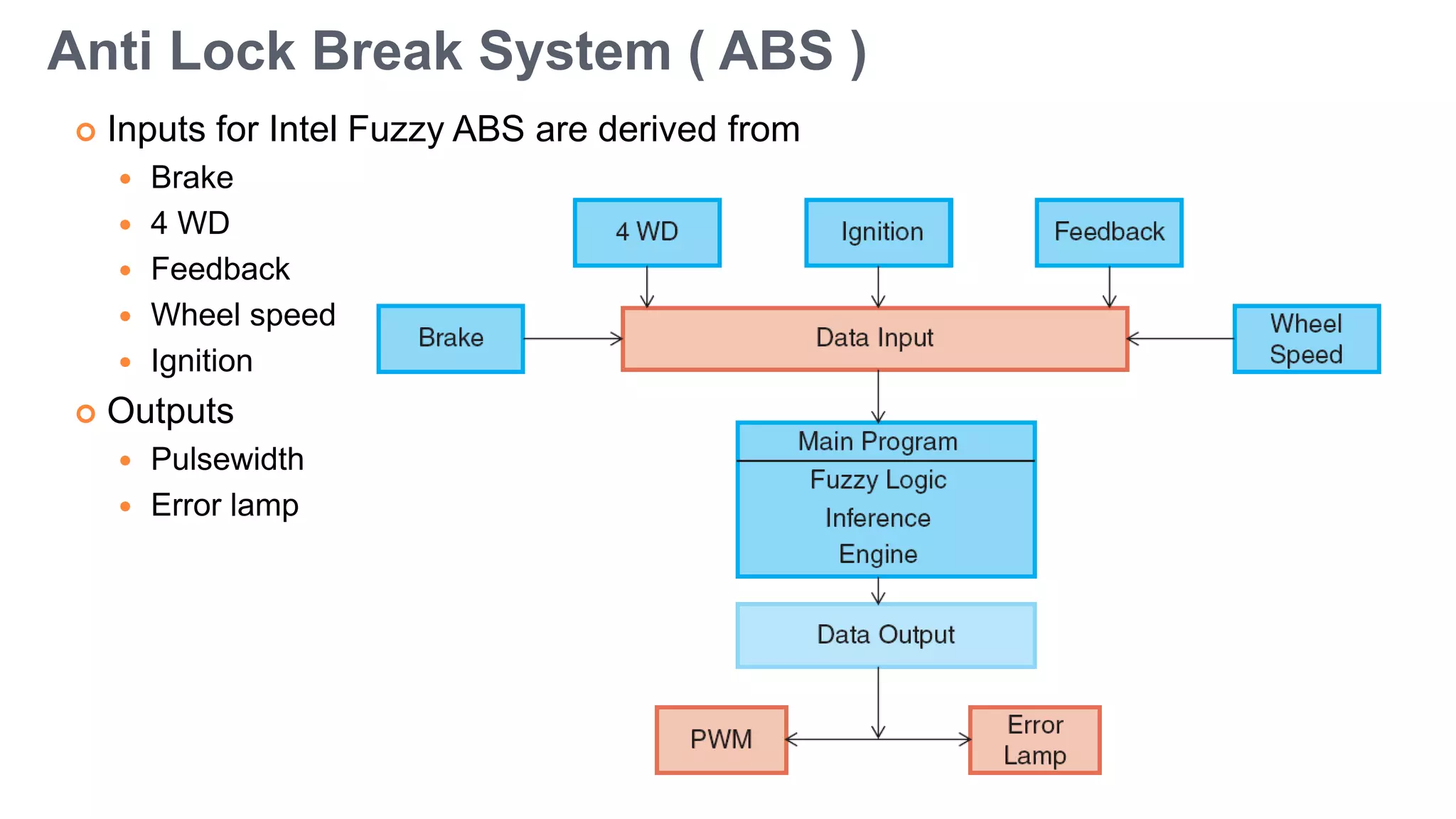
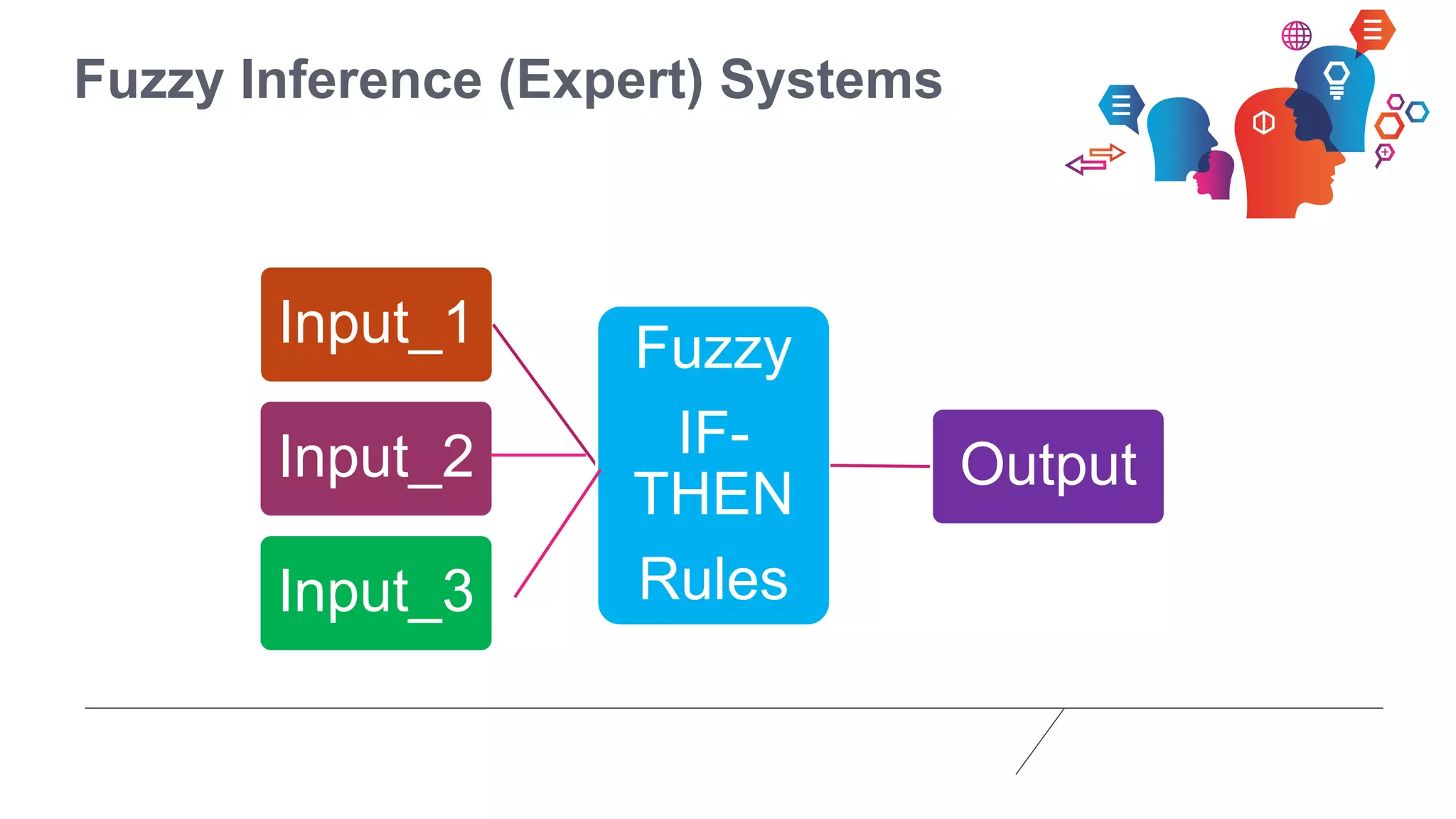
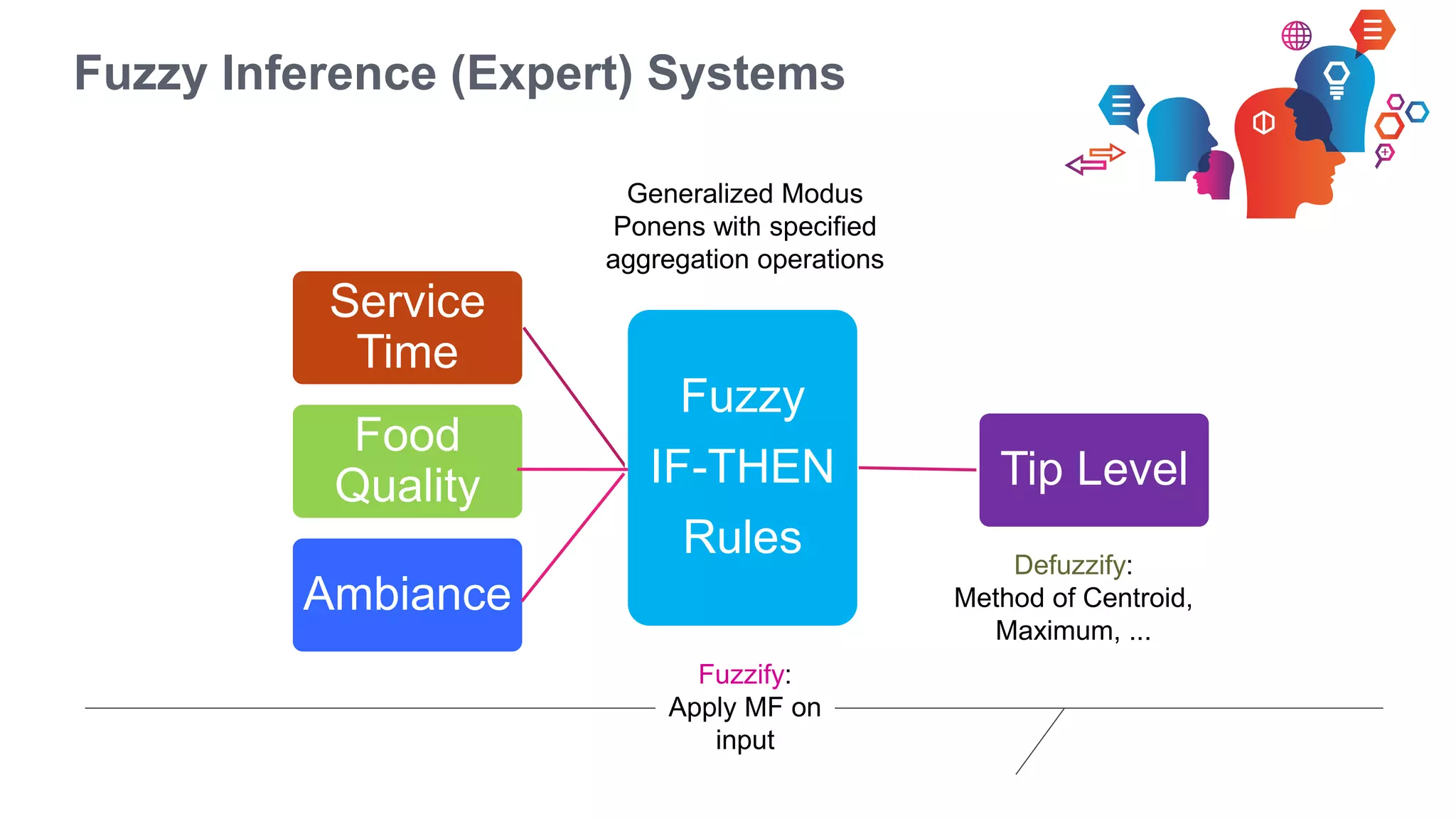
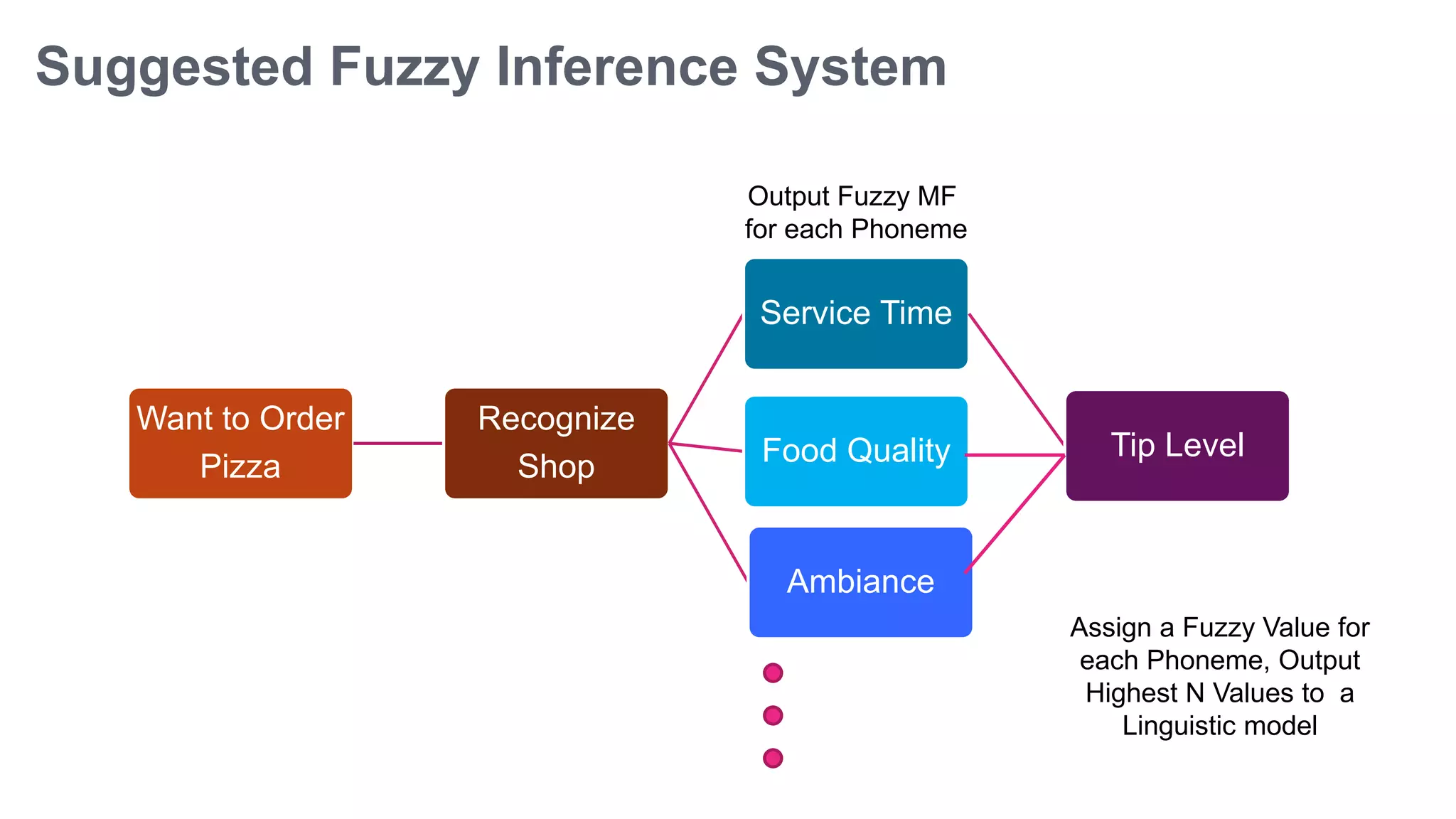
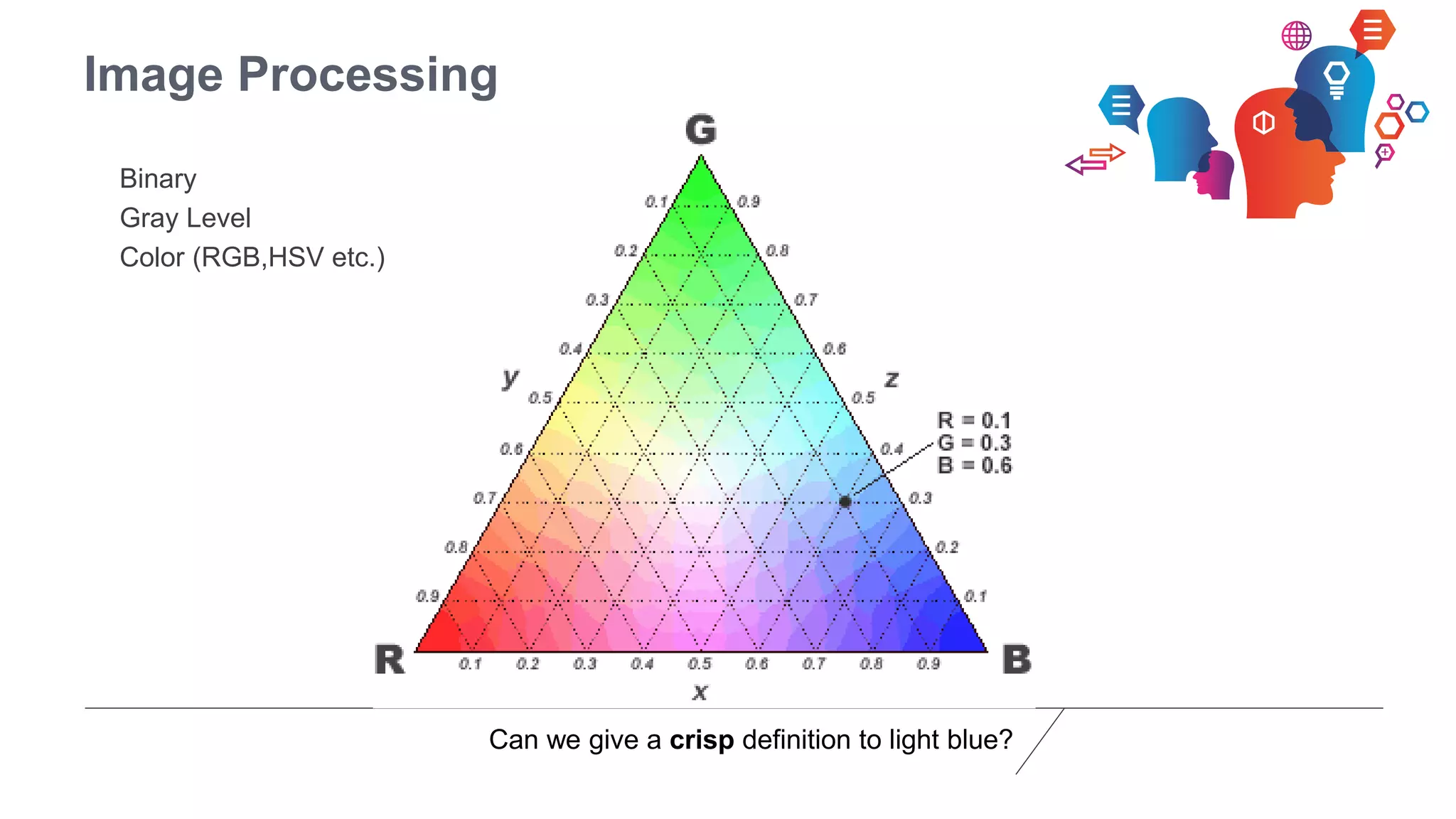
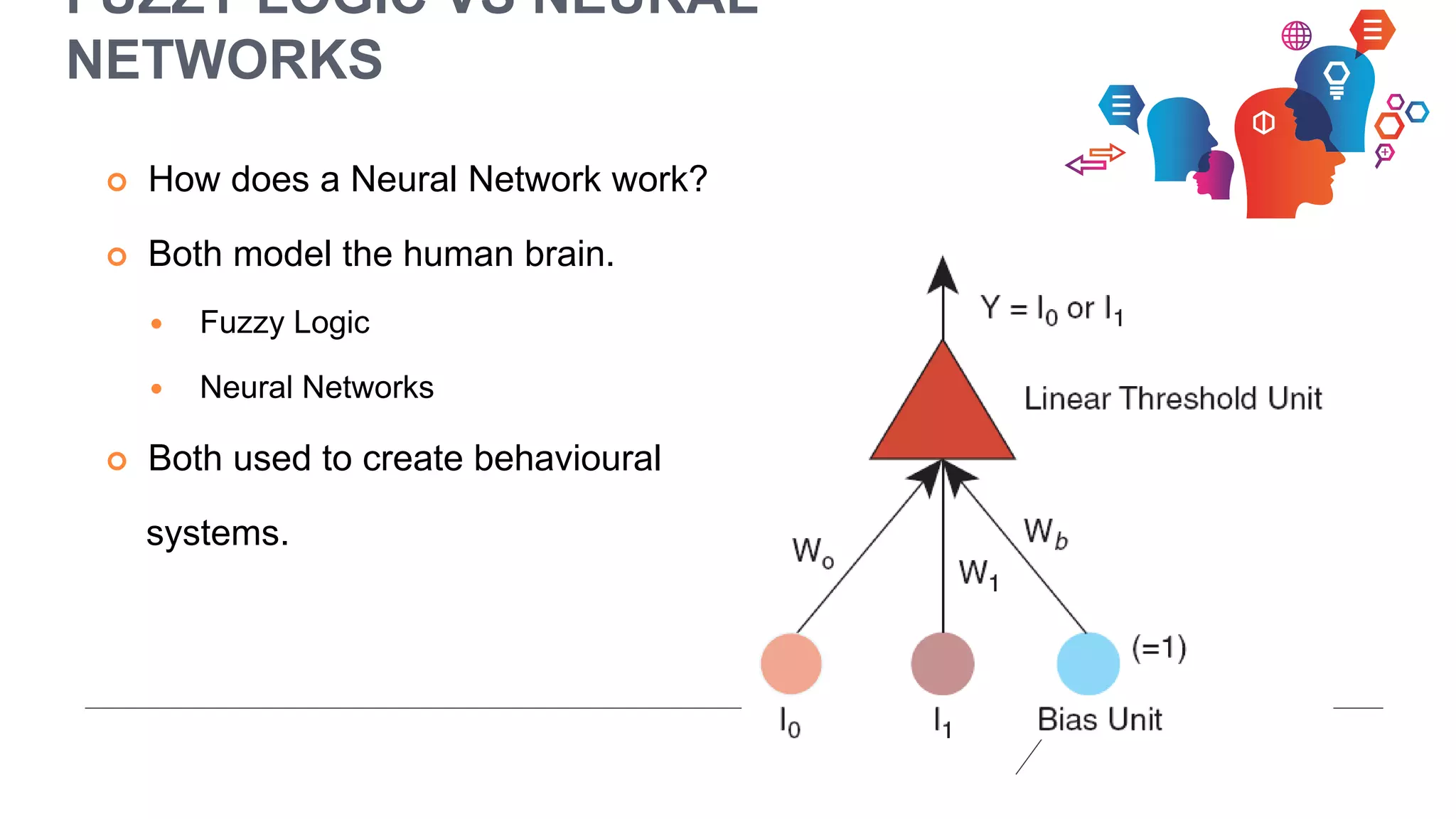
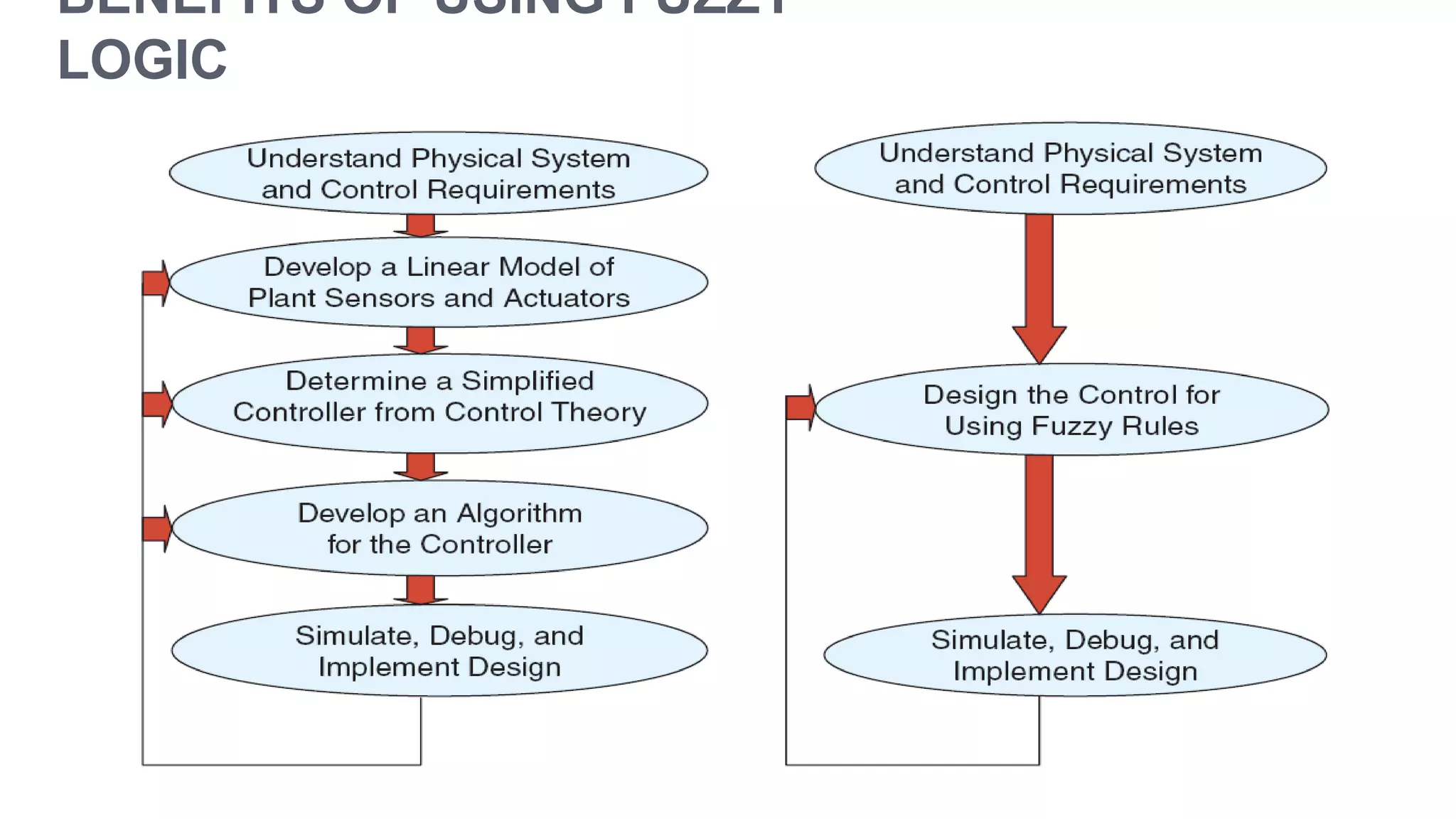
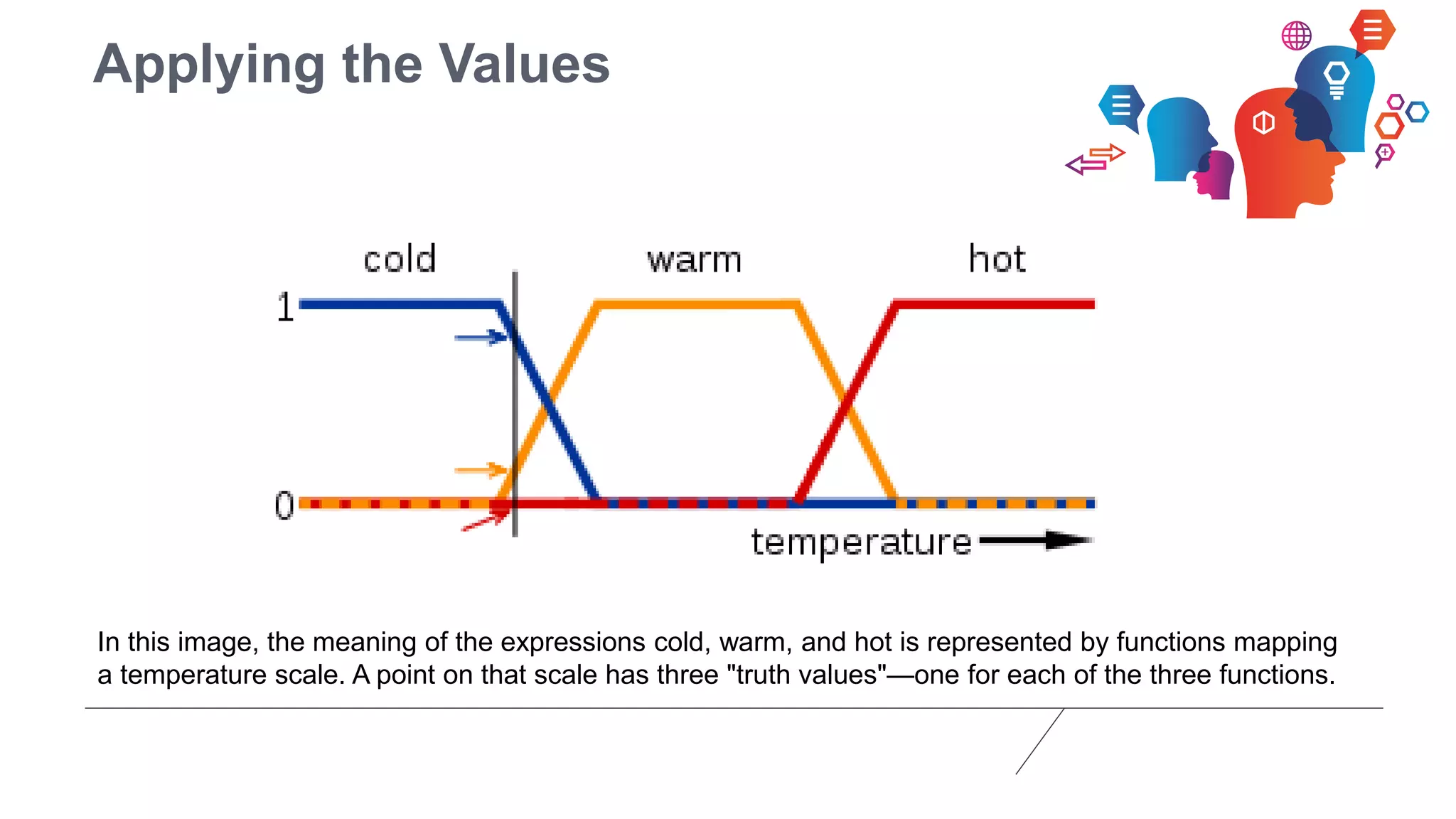
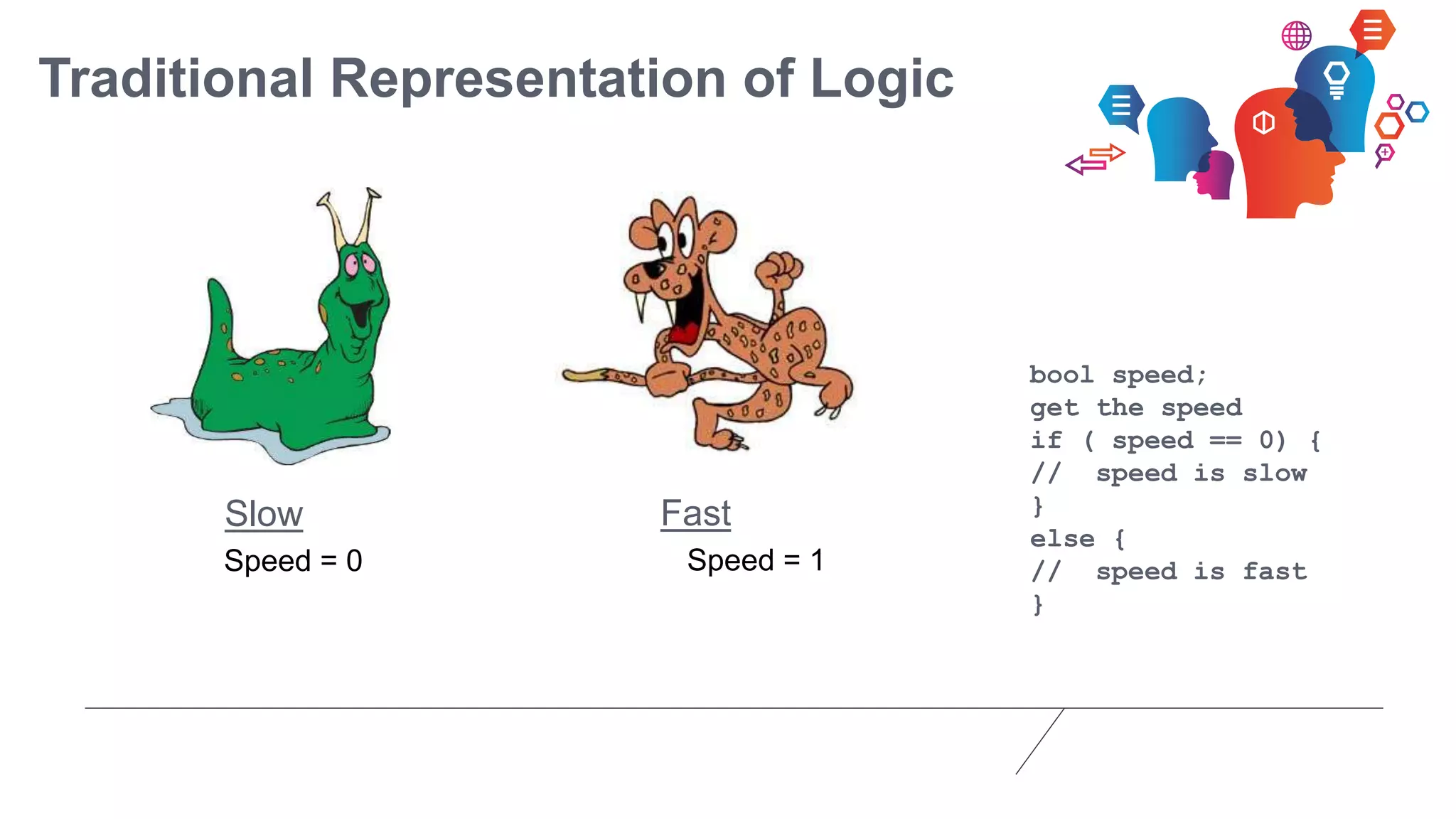
Fuzzy logic is a form of many-valued logic that helps in representing knowledge for ambiguous concepts and is closely aligned with human reasoning. Its applications range from control systems, such as anti-lock brakes and temperature controllers, to expert systems. The technique allows for approximate solutions and processes incomplete data, filling gaps left by traditional binary logic methods.

1. Fuzzy Logic
Intelligent Technique
Qamar Wajid Ali

2. OVERVIEW
 Where did it begin?
 What is Fuzzy Logic?
 Fuzzy Logic in Control Systems
 Fuzzy Logic in Other Fields
 Fuzzy Logic vs. Neural Networks
 Fuzzy Logic Benefits

3. Fuzzy Logic began
 Traces back to Ancient Greece
 Lotfi Asker Zadeh ( 1965 )
 First to publish ideas of fuzzy logic.
 Professor Toshire Terano ( 1972 )
 Organized the world's first working group on fuzzy
systems.
 F.L. Smidth & Co. ( 1980 )
 First to market fuzzy expert systems.

4. WHAT IS FUZZY LOGIC?
 Definition of fuzzy
 Fuzzy – “not clear, distinct, or precise; blurred”
 Definition of fuzzy logic
 A form of knowledge representation suitable for notions that cannot
be defined precisely, but which depend upon their contexts.

5. What is Fuzzy Logic? Contd.
 Fuzzy logic is a form of many-valued logic
 In contrast with traditional logic theory, where binary sets
have two-valued logic:
 true or false,
 completely true or completely false
 0 or 1

6. WHY FUZZY LOGIC
 The reason for the most successful of today's technologies which is very
simple.
 Fuzzy logic addresses such applications perfectly as it resembles human
decision making
 It fills an important gap in engineering design methods left vacant by
purely mathematical approaches (e.g. linear control design), and
purely logic-based approaches (e.g. expert systems) in system
design.

7. WHY FUZZY CONTROL?
 The reasoning in fuzzy logic is similar to human reasoning
 It allows for approximate values and inferences as well as
incomplete or ambiguous data (binary yes/no choices)
 Fuzzy logic is able to process incomplete data and provide
approximate solutions to problems

8. Fuzzy Control Procedure
 Fuzzy control, which directly uses fuzzy rules is the most
important application in fuzzy theory.
 Using a procedure originated by Ebrahim Mamdani in the late
70s, three steps are taken to create a fuzzy controlled machine:
 Fuzzification(Using membership functions to graphically describe a
situation)
 Rule evaluation(Application of fuzzy rules)
 DE-fuzzification(Obtaining the crisp or actual results)

9. Degrees of Truth
 Both degrees of truth and probabilities range between 0 and 1
and hence may seem similar at first. For example, let a
100 ml glass contain 30 ml of water. Then we may consider
two concepts: Empty and Full. The meaning of each of them
can be represented by a certain fuzzy set.
 Then one might define the glass as being 0.7 empty and 0.3
full

10. Applying the Values
In this image, the meaning of the expressions cold, warm, and hot is represented by functions mapping
a temperature scale. A point on that scale has three "truth values"—one for each of the three functions.

11. Fig. below illustrates bivalent sets to characterize the temperature of a
room
Example

12. Traditional Representation of Logic
Slow Fast
Speed = 0 Speed = 1
bool speed;
get the speed
if ( speed == 0) {
// speed is slow
}
else {
// speed is fast
}

13. Fuzzy Logic Representation
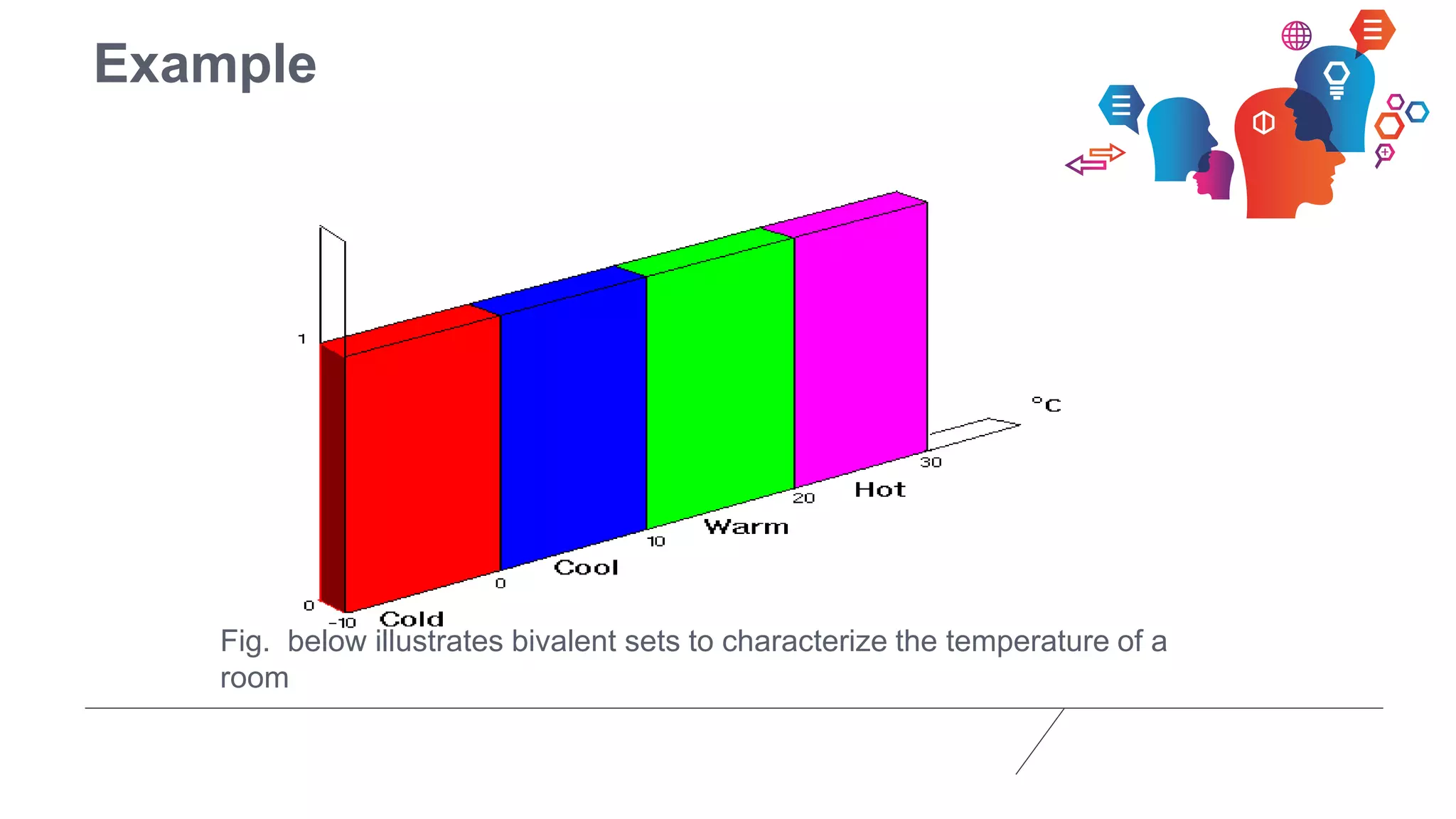
 For every problem must represent in terms of fuzzy sets
 What are fuzzy sets?
Slowest Fastes
t
Slow Fast
[ 0.0 – 0.25 ] [ 0.25 – 0.50
]
[ 0.50 – 0.75
]
[ 0.75 – 1.00
]

14. Fuzzy Logic Representation Cont.
Slowest Fastest
float speed;
get the speed
if ((speed >= 0.0)&&(speed < 0.25)) {
// speed is slowest
}
else if ((speed >= 0.25)&&(speed <
0.5))
{
// speed is slow
}
Slow Fast
else if ((speed >= 0.5)&&(speed < 0.75))
{
// speed is fast
}
else // speed >= 0.75 && speed < 1.0
{
// speed is fastest
}

15. How do fuzzy sets differ from classical
sets?
 In classical set theory we assume that all sets rare well-defined (or
crisp), that is given any object in our universe we can always say that
object either is or is not the member of a particular set.
 CLASSICAL SETS
 The set of people that can run a mile in 4 minutes or less.
 The set of children under age seven that weigh more than 1oo pounds.
 FUZZY SETS
 The set of fast runners
 The set of overweight children

16. Applications
 ABS Brakes
 Expert Systems
 Control Units
 Bullet train between Tokyo and Osaka
 Video Cameras
 Automatic Transmissions
 Washing Machines

17. Fuzzy Controllers
• Used to control a physical system

18. TEMPERATURE CONTROLLER
 A temperature control system has four settings
 Cold, Cool, Warm, and Hot
Change the speed of a heater fan, based off the room temperature and humidity.

19. Anti Lock Break System ( ABS )
 Inputs for Intel Fuzzy ABS are derived from
 Brake
 4 WD
 Feedback
 Wheel speed
 Ignition
 Outputs
 Pulsewidth
 Error lamp

20. Fuzzy Inference (Expert) Systems
Input_1 Fuzzy
IF-
THEN
Rules
OutputInput_2
Input_3

21. Service
Time
Fuzzy
IF-THEN
Rules
Tip Level
Ambiance
Food
Quality
Fuzzy Inference (Expert) Systems
Fuzzify:
Apply MF on
input
Generalized Modus
Ponens with specified
aggregation operations
Defuzzify:
Method of Centroid,
Maximum, ...

22. Suggested Fuzzy Inference System
Want to Order
Pizza
Recognize
Shop
Service Time
Tip LevelFood Quality
Ambiance
Output Fuzzy MF
for each Phoneme
Assign a Fuzzy Value for
each Phoneme, Output
Highest N Values to a
Linguistic model

23. Image Processing
Binary
Gray Level
Color (RGB,HSV etc.)
Can we give a crisp definition to light blue?

24. FUZZY LOGIC VS NEURAL
NETWORKS
 How does a Neural Network work?
 Both model the human brain.
 Fuzzy Logic
 Neural Networks
 Both used to create behavioural
systems.

25. BENEFITS OF USING FUZZY
LOGIC