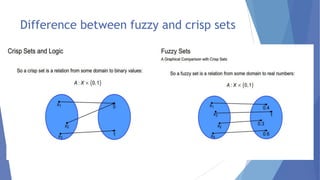
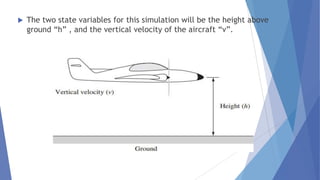
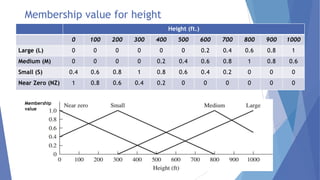
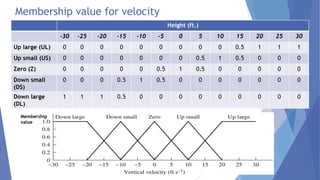
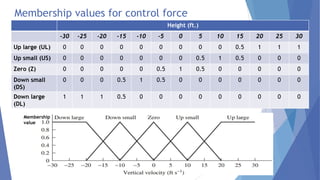
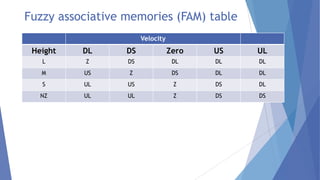
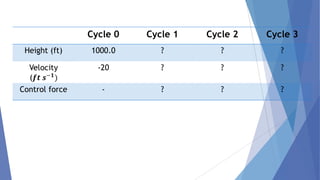
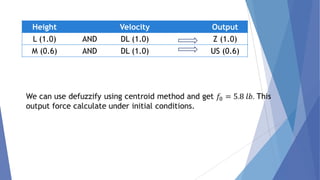
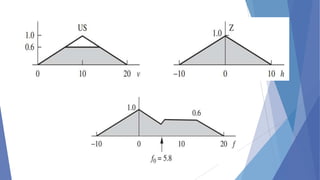
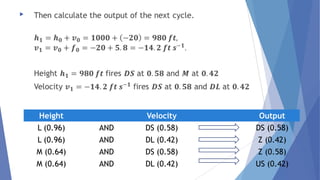
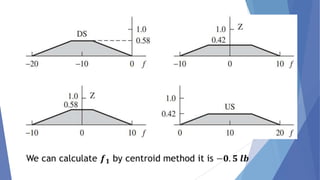
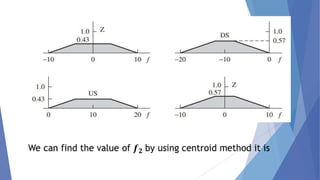
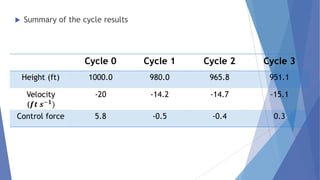
This document describes a study conducted by undergraduate students at Uva Wellassa University of Sri Lanka on applying fuzzy logic to aircraft landing control. It provides background on fuzzy logic and fuzzy set theory. It then presents the students' simulation of an aircraft's final descent and landing approach, where fuzzy logic is used to control the aircraft's vertical velocity based on its current height above ground. Over multiple cycles, the simulation demonstrates how the fuzzy logic system gradually reduces the aircraft's velocity as it gets closer to landing for a soft touchdown.

1. Fuzzy logic applications
Aircraft landing control
Uva Wellassa University of Sri Lanka

2. Group Members…

Samarathunga S.M.B.P.B.

Karunarathna R.M.C.P.

Thennakoon H.M.D.J.

Somasiri K.G.H.A.

3. What is fuzzy logic?
There are many areas of uncertainty or fuzziness in real world
systems and an efficient way of dealing with this fuzziness is
by the mechanism of fuzzy logic.
Owing to its ease of implementation and robustness, fuzzy
logic control (FLC) is increasingly growing in popularity among
control engineers.
Fuzzy logic relates to the way of people think and talk, in
other words, their use of natural language.

4. Difference between fuzzy and crisp sets

5. Fuzzy Logic applications

Power system stability controllers.

Temperature controller.

Anti lock break system(ABS).

Hybrid modelling.

Fuzzy controlled washing machine.

Air Condition machine.

6. Aircraft Landing Control Problem

We will conduct a simulation of the final descent and landing approach of
an aircraft.

The desired downward velocity is proportional to the square of the
height. Thus, at higher altitudes, a large downward velocity is desired.

As the height (altitude) diminishes, the desired downward velocity gets
smaller and smaller.

In the limit, as the height becomes vanishingly small, the downward
velocity also goes to zero.

In this way, the aircraft will descend from altitude promptly but will touch
down very gently to avoid damage.

7. 
The two state variables for this simulation will be the height above
ground “h” , and the vertical velocity of the aircraft “v”.

8. 

9. 

10. Membership value for height
Height (ft.)
0
100
200
300
400
500
600
700
800
900
1000
Large (L)
0
0
0
0
0
0
0.2
0.4
0.6
0.8
1
Medium (M)
0
0
0
0
0.2
0.4
0.6
0.8
1
0.8
0.6
0.4
0.6
0.8
1
0.8
0.6
0.4
0.2
0
0
0
1
0.8
0.6
0.4
0.2
0
0
0
0
0
0
Small (S)
Near Zero (NZ)
Membership
value

11. Membership value for velocity
Height (ft.)
-30
-25
-20
-15
-10
-5
0
5
10
15
20
25
30
Up large (UL)
0
0
0
0
0
0
0
0
0
0.5
1
1
1
Up small (US)
0
0
0
0
0
0
0
0.5
1
0.5
0
0
0
Zero (Z)
0
0
0
0
0
0.5
1
0.5
0
0
0
0
0
Down small
(DS)
0
0
0
0.5
1
0.5
0
0
0
0
0
0
0
Down large
(DL)
1
1
1
0.5
0
0
0
0
0
0
0
0
0
Membership
value

12. Membership values for control force
Height (ft.)
-30
-25
-20
-15
-10
-5
0
5
10
15
20
25
30
Up large (UL)
0
0
0
0
0
0
0
0
0
0.5
1
1
1
Up small (US)
0
0
0
0
0
0
0
0.5
1
0.5
0
0
0
Zero (Z)
0
0
0
0
0
0.5
1
0.5
0
0
0
0
0
Down small
(DS)
0
0
0
0.5
1
0.5
0
0
0
0
0
0
0
Down large
(DL)
1
1
1
0.5
0
0
0
0
0
0
0
0
0
Membership
value

13. Fuzzy associative memories (FAM) table
Velocity
Height
DL
DS
Zero
US
UL
L
Z
DS
DL
DL
DL
M
US
Z
DS
DL
DL
S
UL
US
Z
DS
DL
NZ
UL
UL
Z
DS
DS

14. Cycle 0
Control force
Cycle 2
Cycle 3
1000.0
?
?
?
-20
Height (ft)
Cycle 1
?
?
?
-
?
?
?

15. 

16. Height
L (1.0)
M (0.6)
Velocity
AND
AND
Output
DL (1.0)
DL (1.0)
Z (1.0)
US (0.6)

18. 
Height
L (0.96)
L (0.96)
M (0.64)
M (0.64)
AND
AND
AND
AND
Velocity
DS (0.58)
DL (0.42)
DS (0.58)
DL (0.42)
Output
DS (0.58)
Z (0.42)
Z (0.58)
US (0.42)

20. 
Height
L (0.93)
L (0.93)
M (0.67)
M (0.67)
AND
AND
Velocity
DL (0.43)
DS (0.57)
Output
Z (0.43)
DS (0.57)
AND
AND
DL (0.43)
DS (0.57)
US (0.43)
Z (0.57)

22. 

23. 
Summary of the cycle results
Cycle 0
Control force
Cycle 2
Cycle 3
1000.0
980.0
965.8
951.1
-20
Height (ft)
Cycle 1
-14.2
-14.7
-15.1
5.8
-0.5
-0.4
0.3

24. 
Summary of the cycle results
Cycle 0
Control force
Cycle 2
Cycle 3
1000.0
980.0
965.8
951.1
-20
Height (ft)
Cycle 1
-14.2
-14.7
-15.1
5.8
-0.5
-0.4
0.3

25. References…

Ross, T.J., 2010, FUZZY LOGIC WITH ENGINEERING APPLICATIONS, 3rd edition,
John Wiley & Sons, Ltd..

Sisil Kumarawadu, 2010, CONTROL SYSTEMS Theory and Implementations,
Narosa Publishing House.