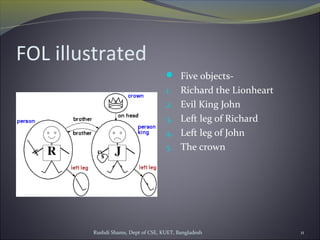
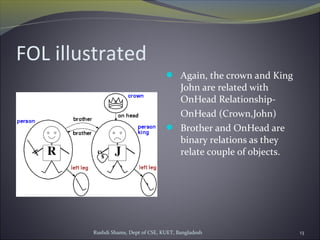
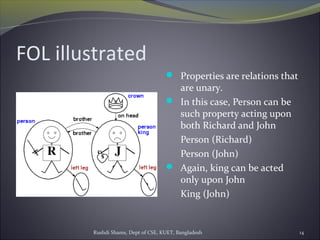
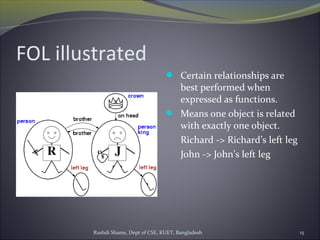
The document discusses first-order logic (FOL) and its advantages over propositional logic for representing knowledge. It introduces the basic elements of FOL syntax, such as constants, predicates, functions, variables, and connectives. It provides examples of FOL expressions and discusses how objects and relations between objects can be represented. It also covers quantification in FOL using universal and existential quantifiers.


















![Order of application of quantifiers
When more than one variables are quantified in a wff
such as ∃ y ∀ x P( x, y ), they are applied from the
inside, that is, the one closest to the atomic formula is
applied first.
Thus ∃ y ∀ x P( x, y ) reads ∃ y [∀ x P( x, y )], and
we say "there exists a y such that for every x, P( x,
y ) holds" or "for some y, P( x, y ) holds for every x".
Rushdi Shams, Dept of CSE, KUET, Bangladesh 23](https://image.slidesharecdn.com/firstorderlogic-130930084554-phpapp01/85/First-order-logic-23-320.jpg)

























