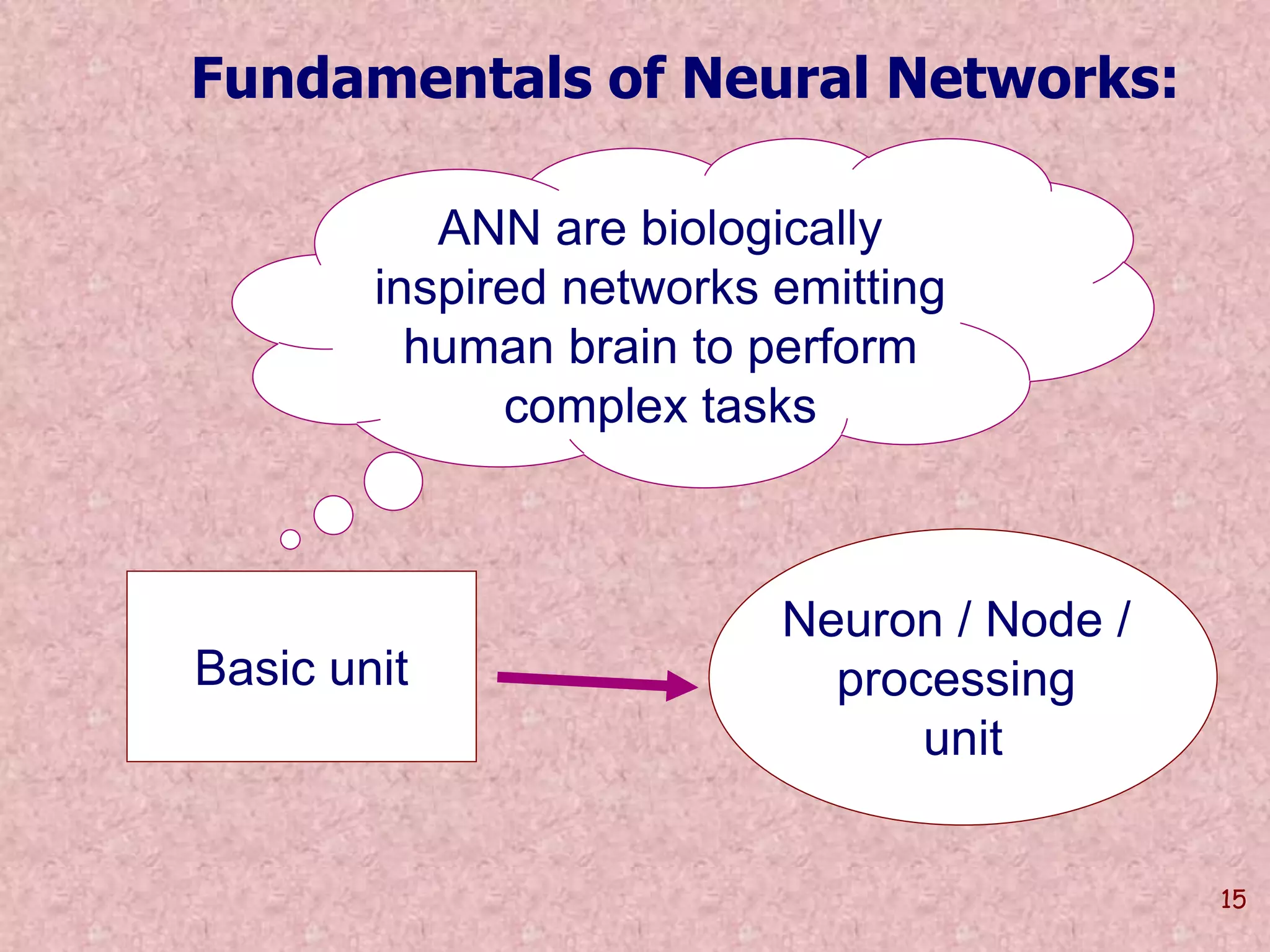
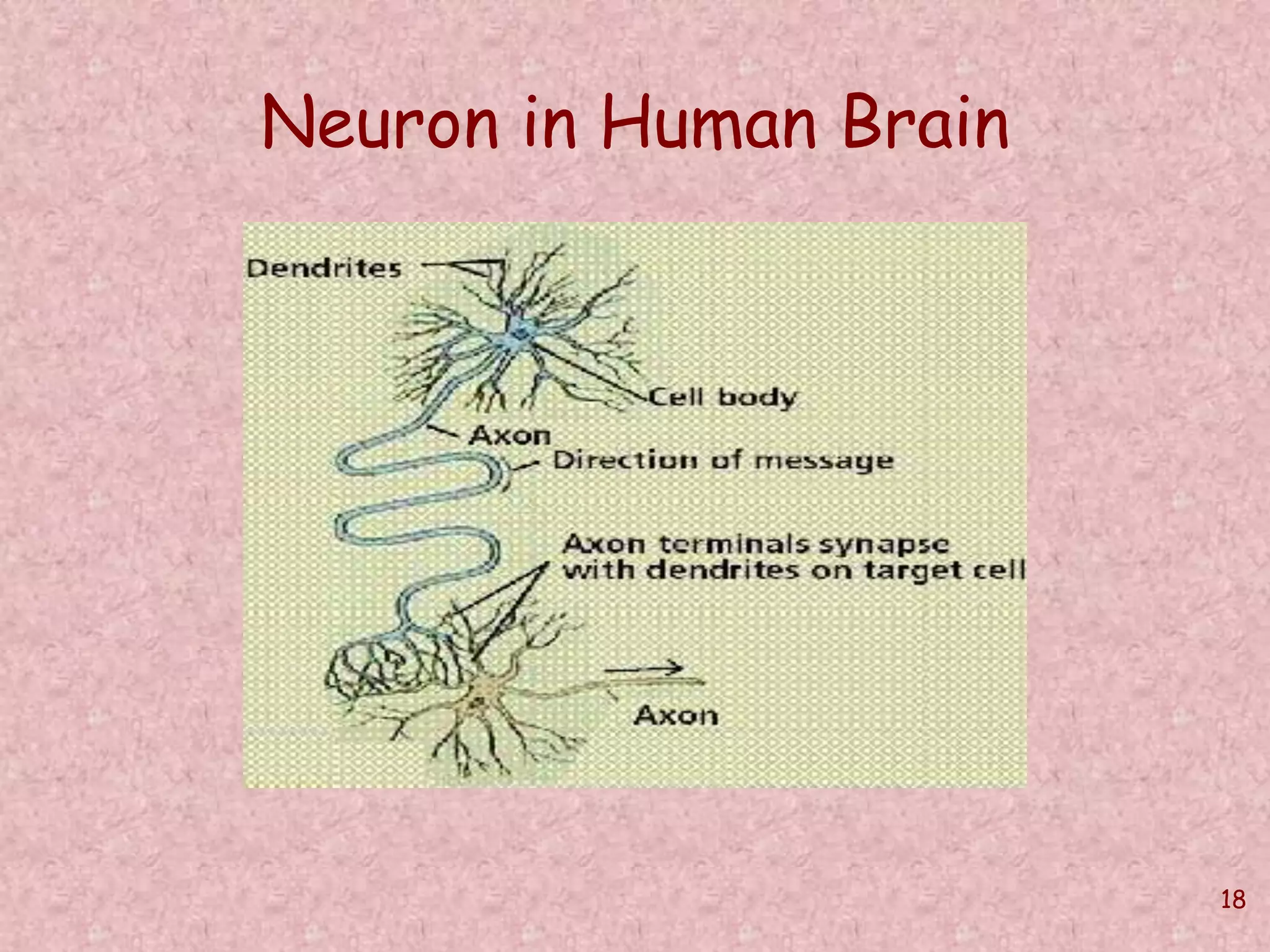
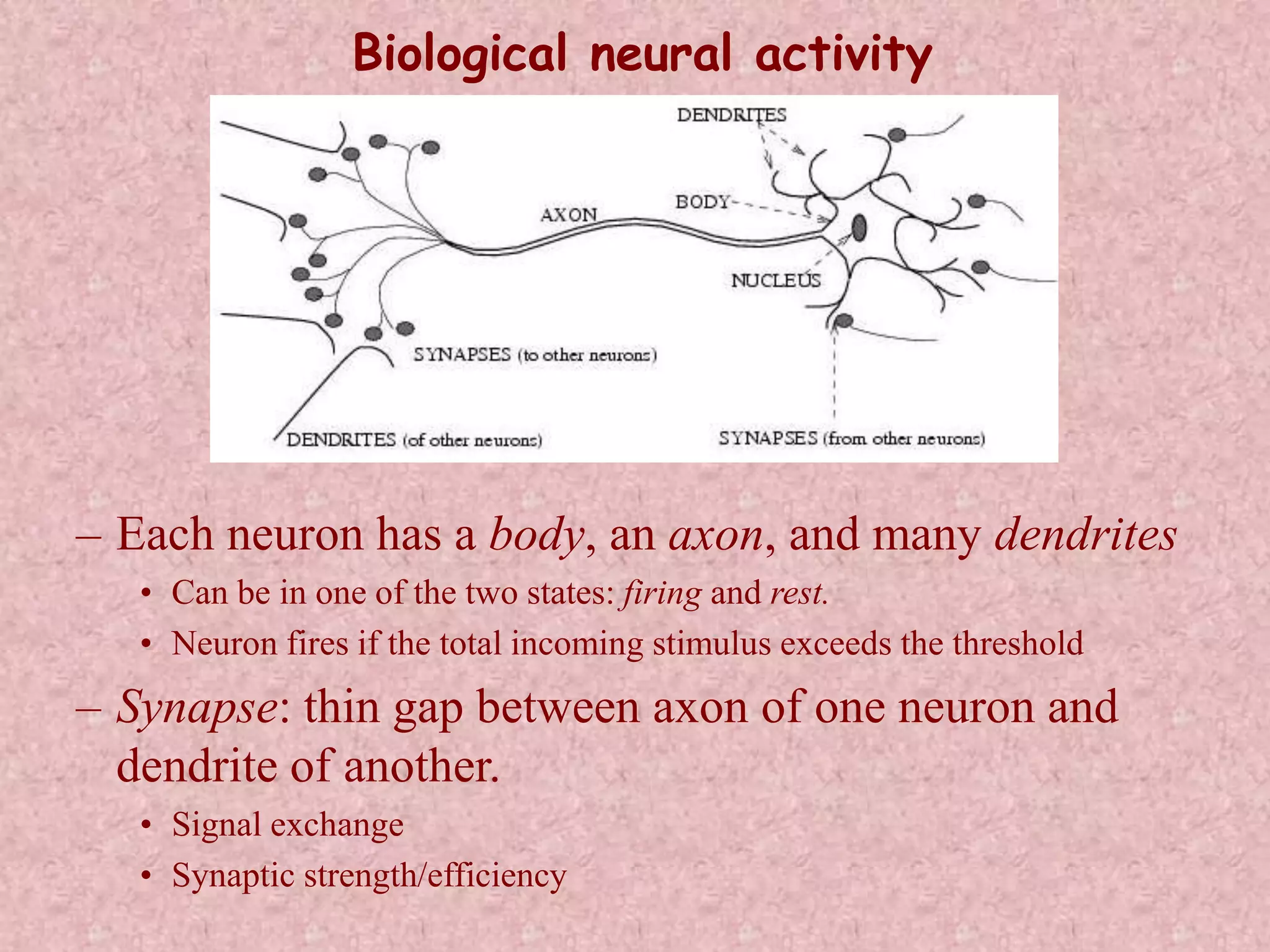
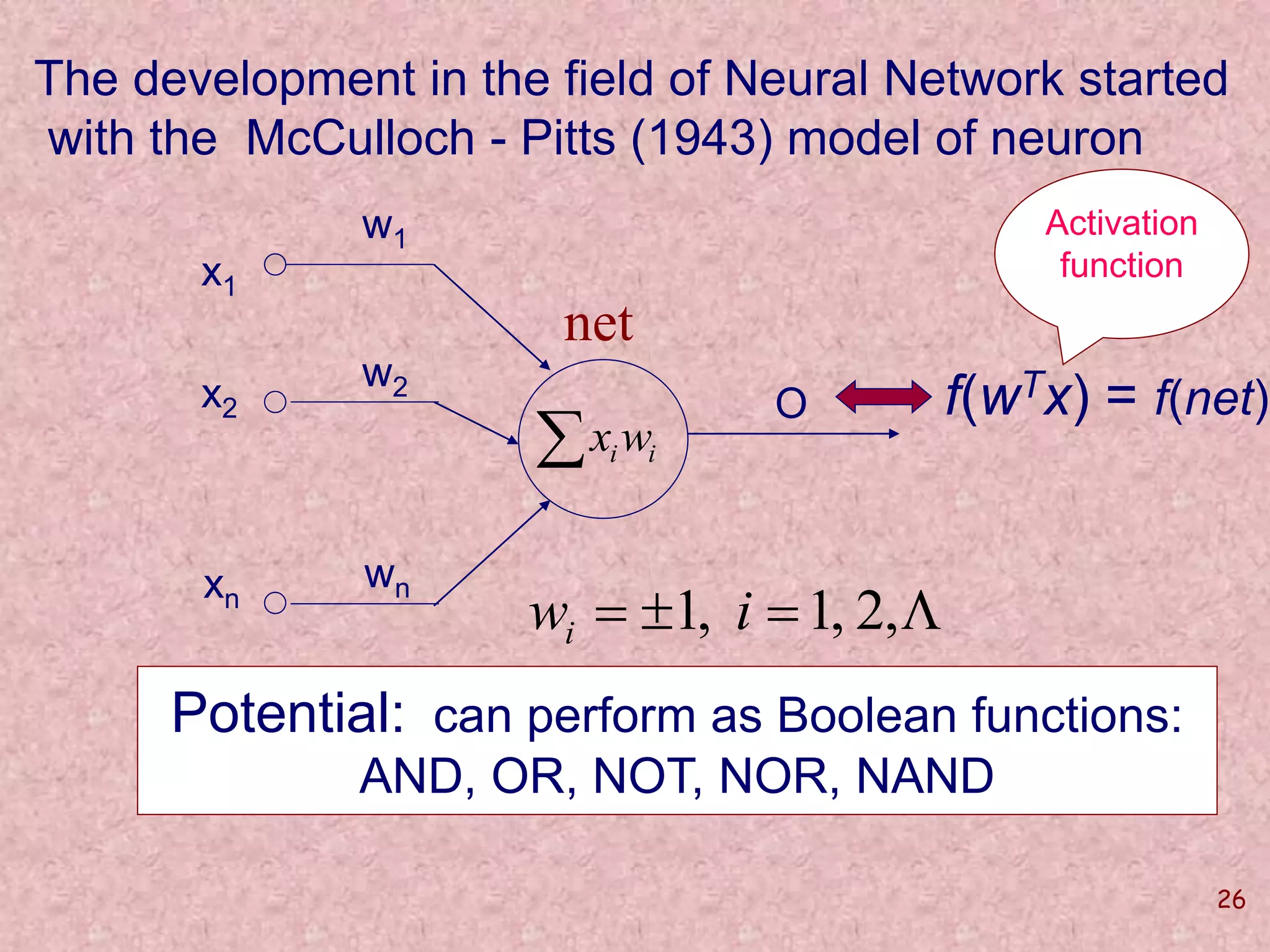
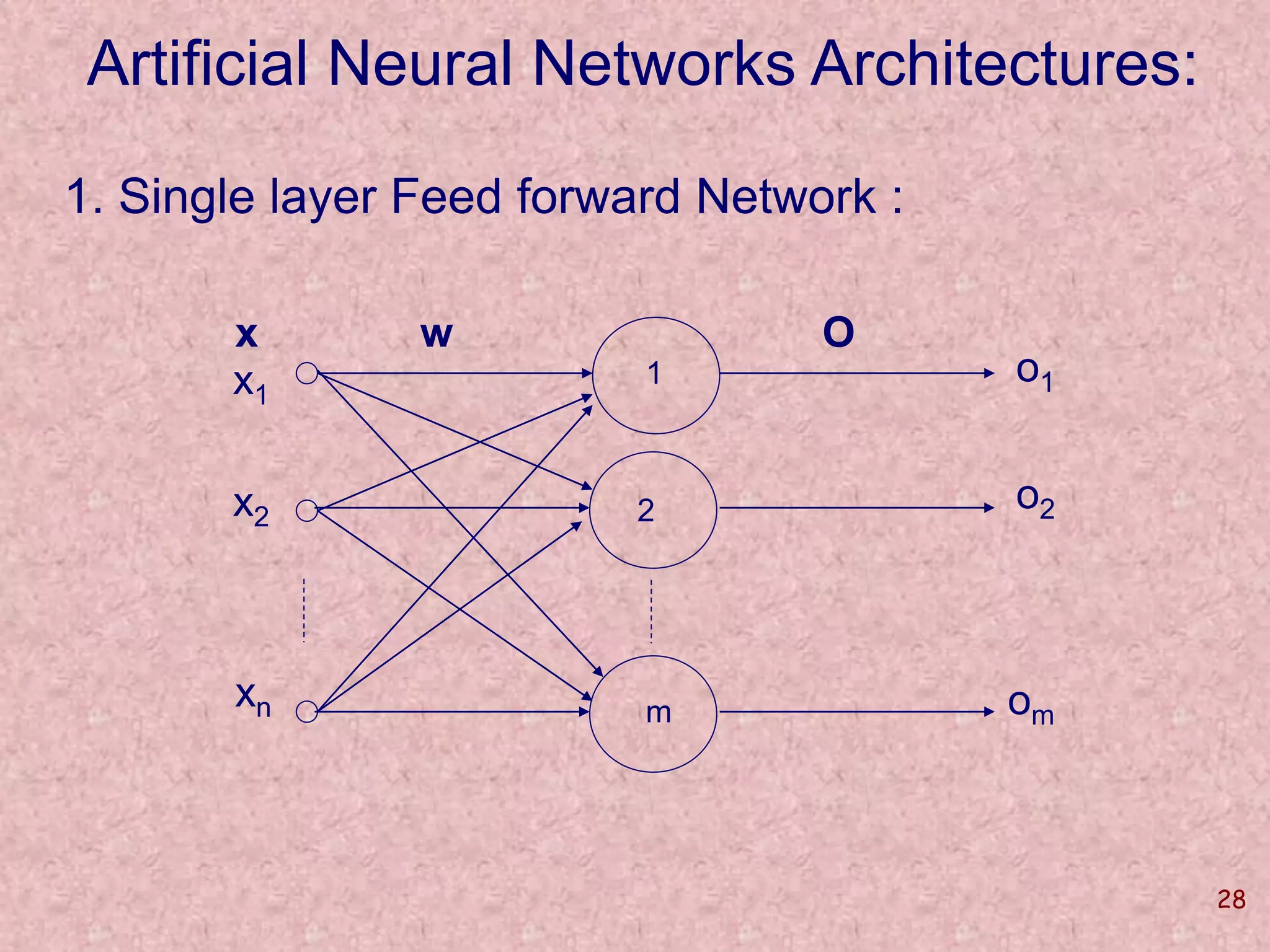
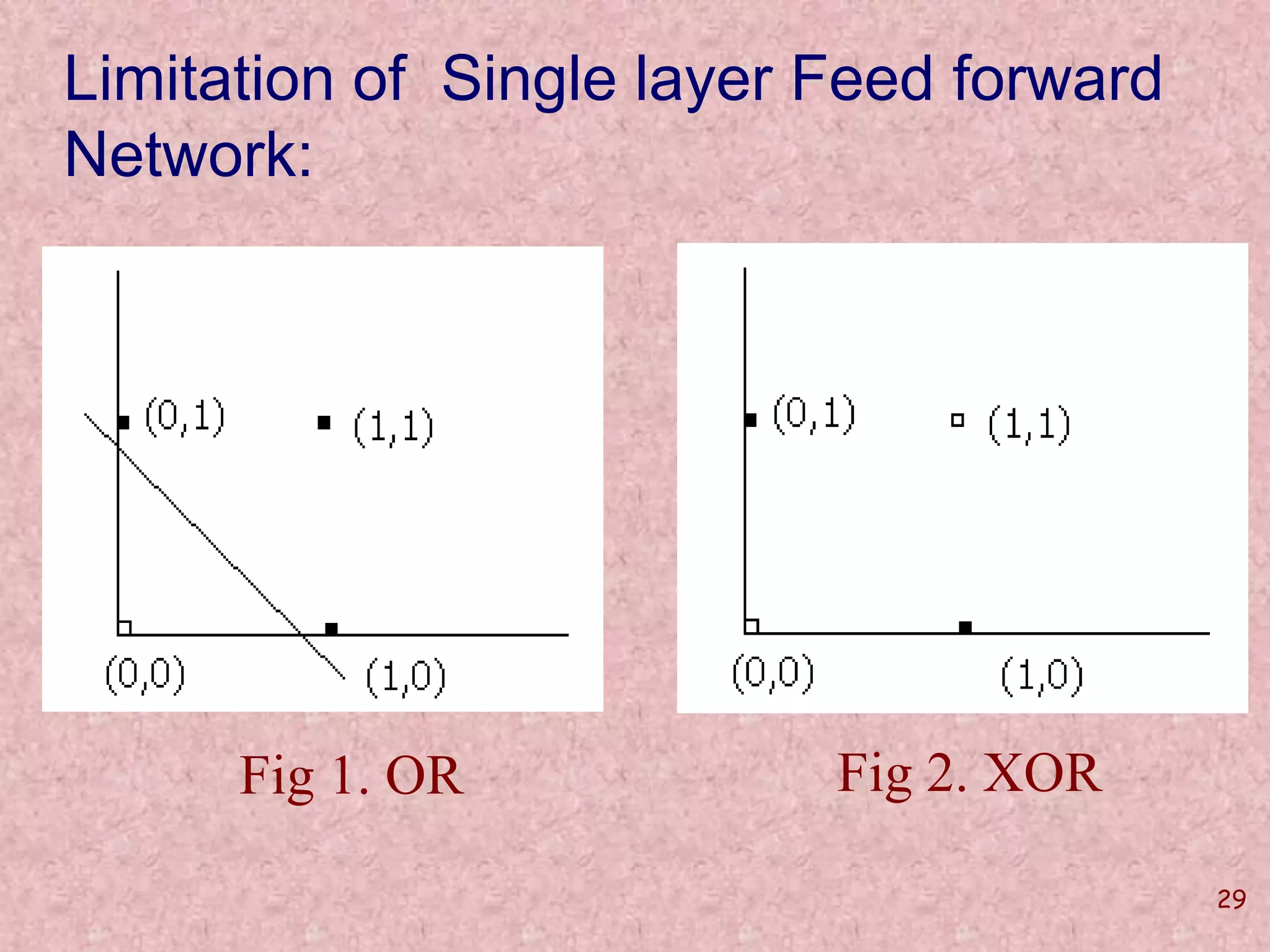
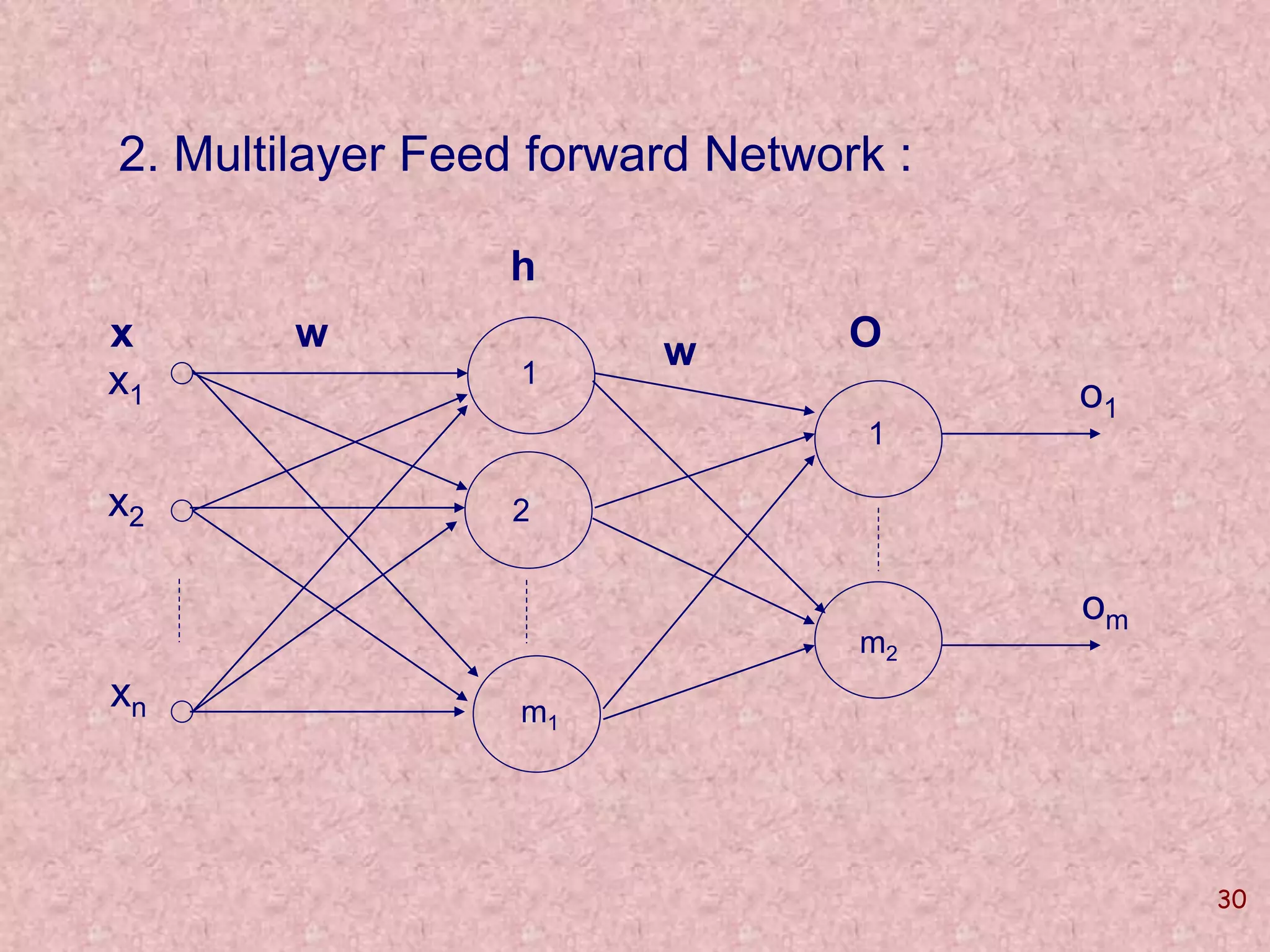
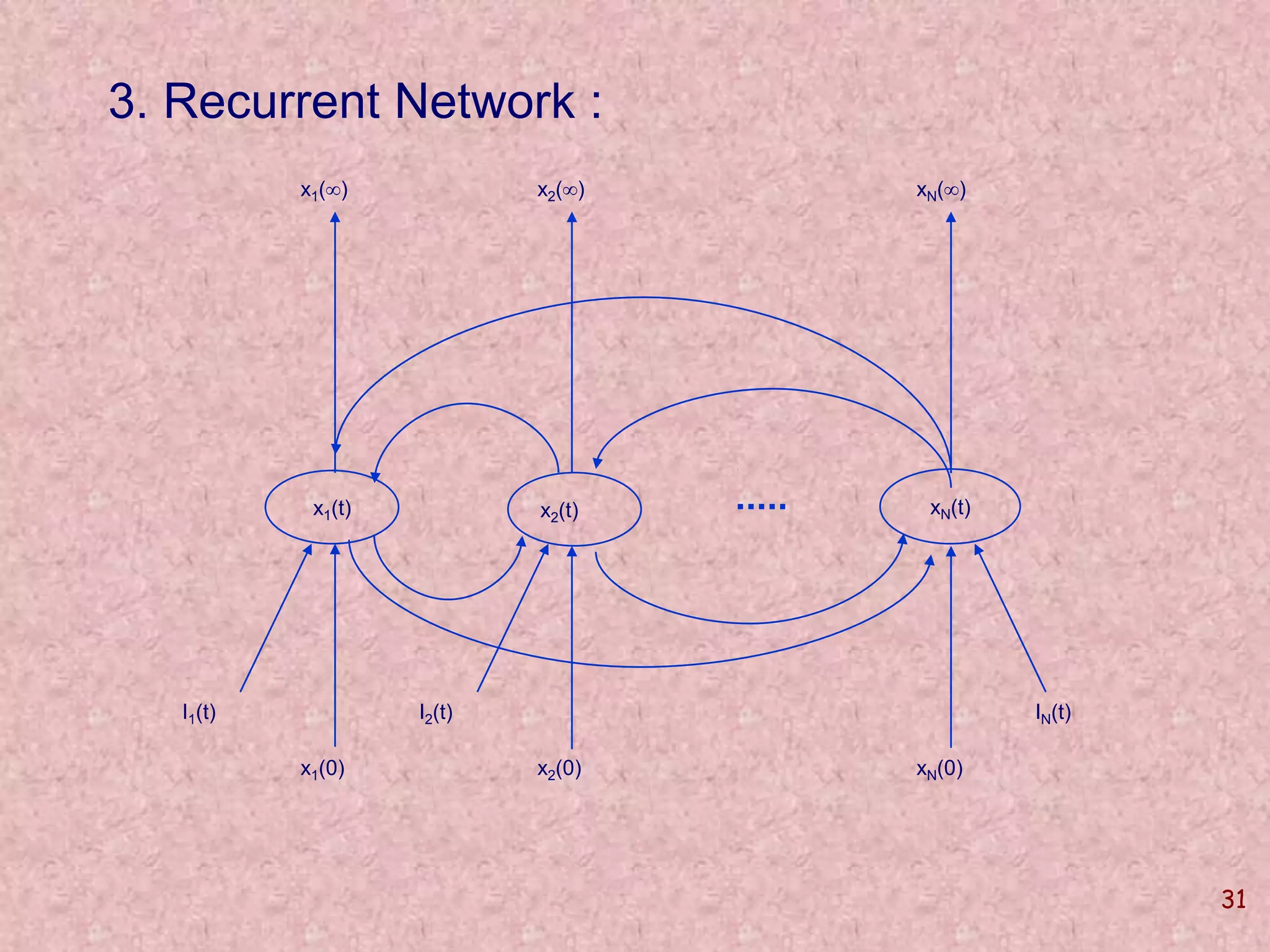
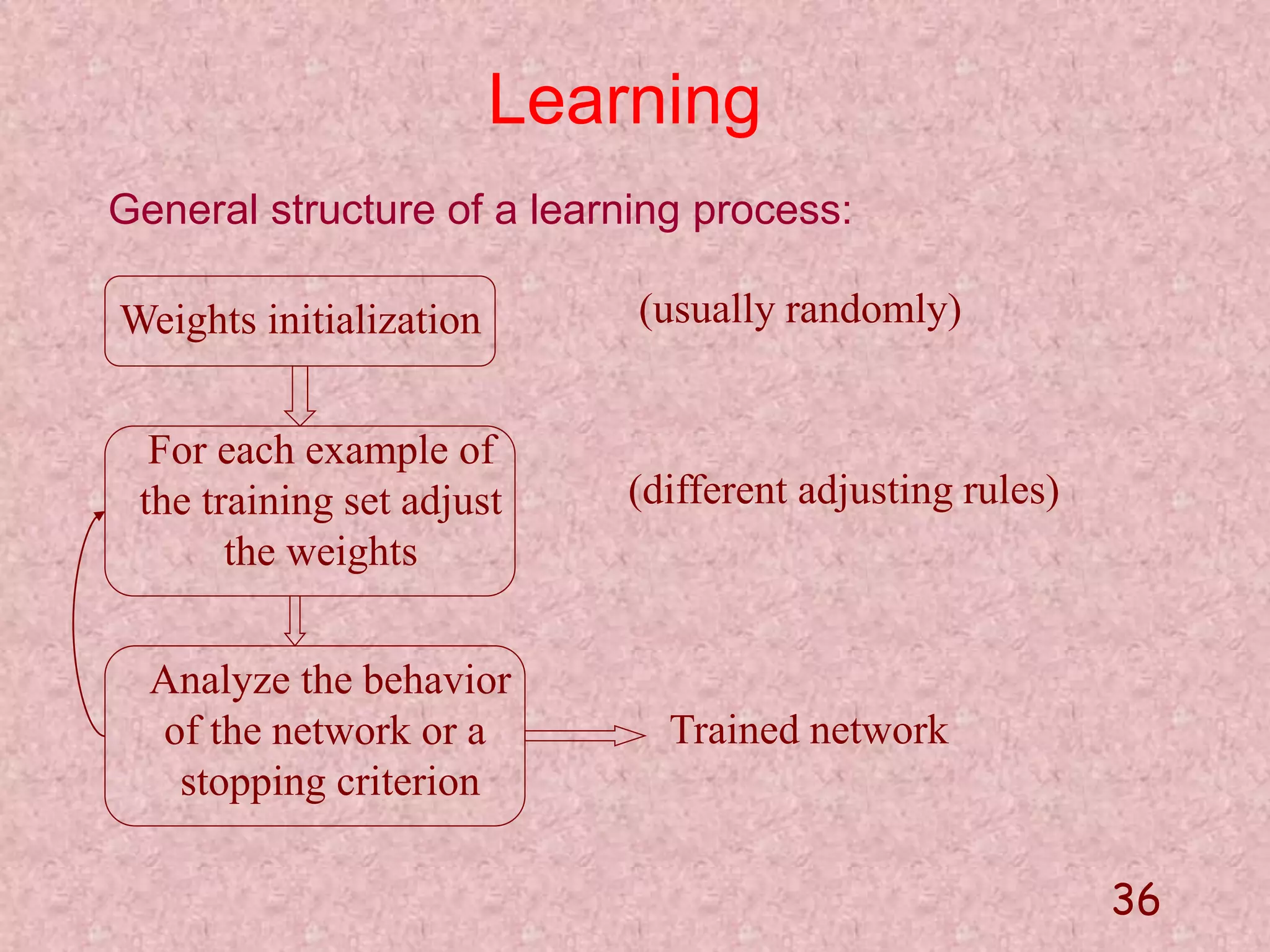
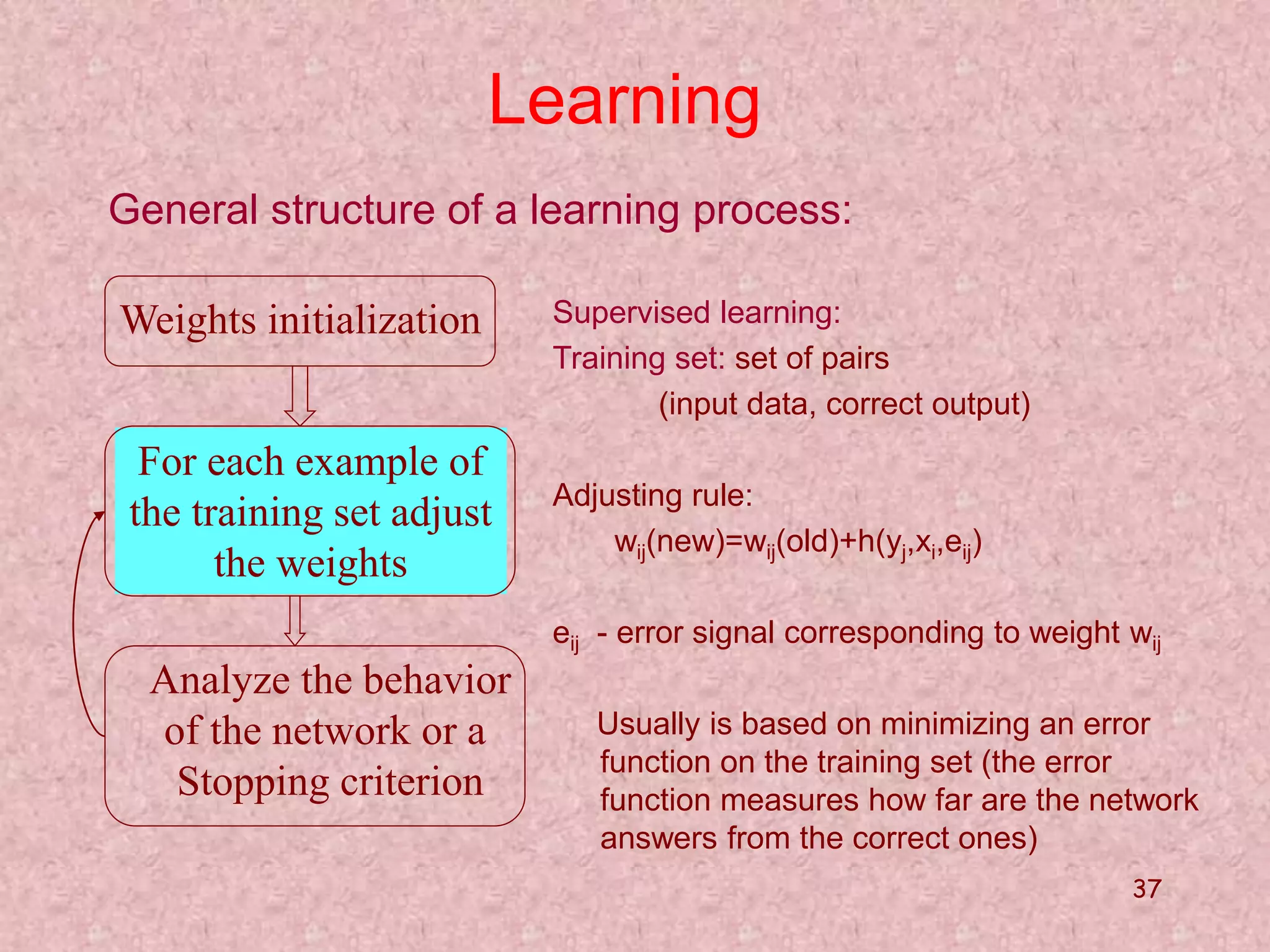
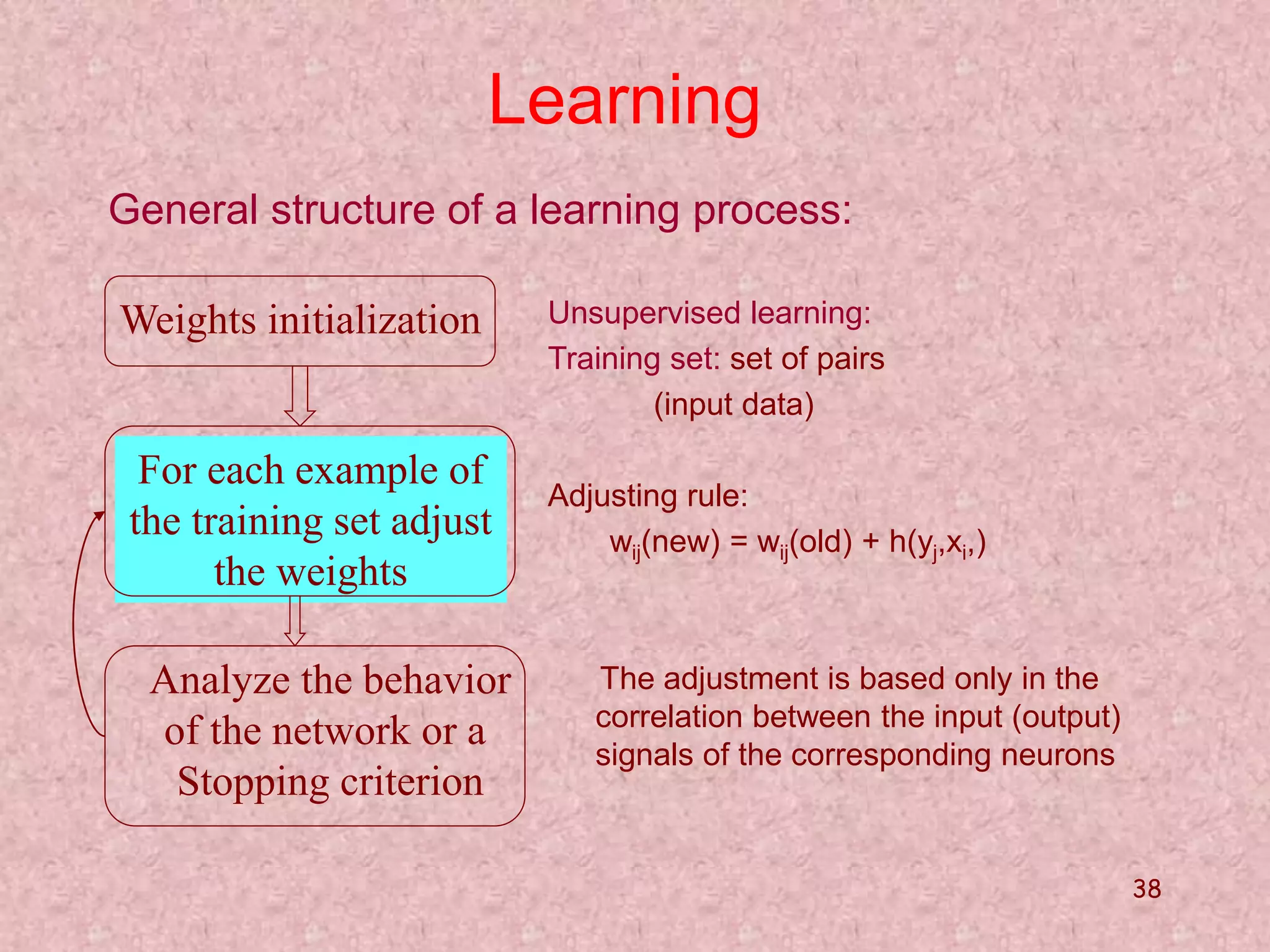
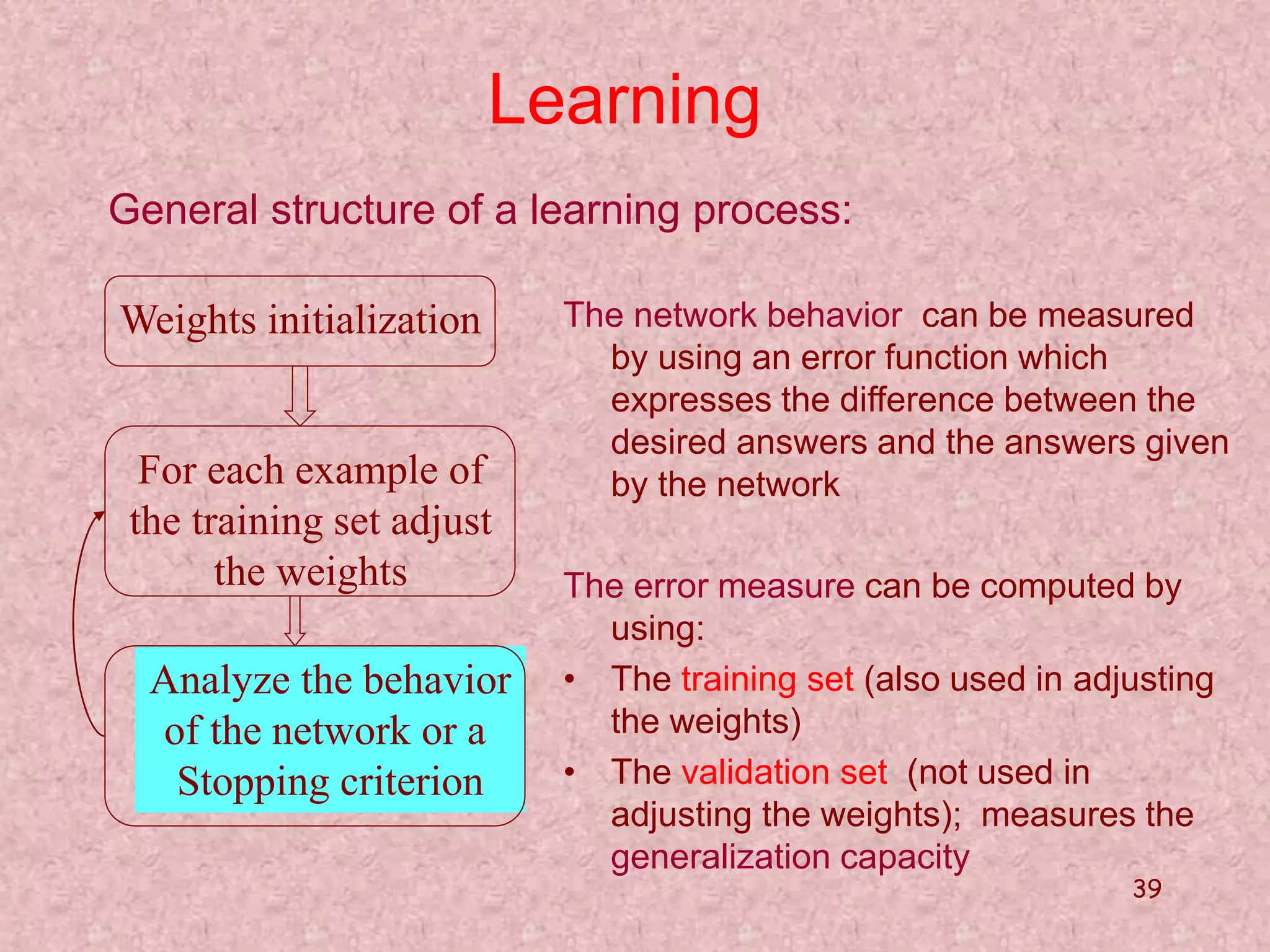
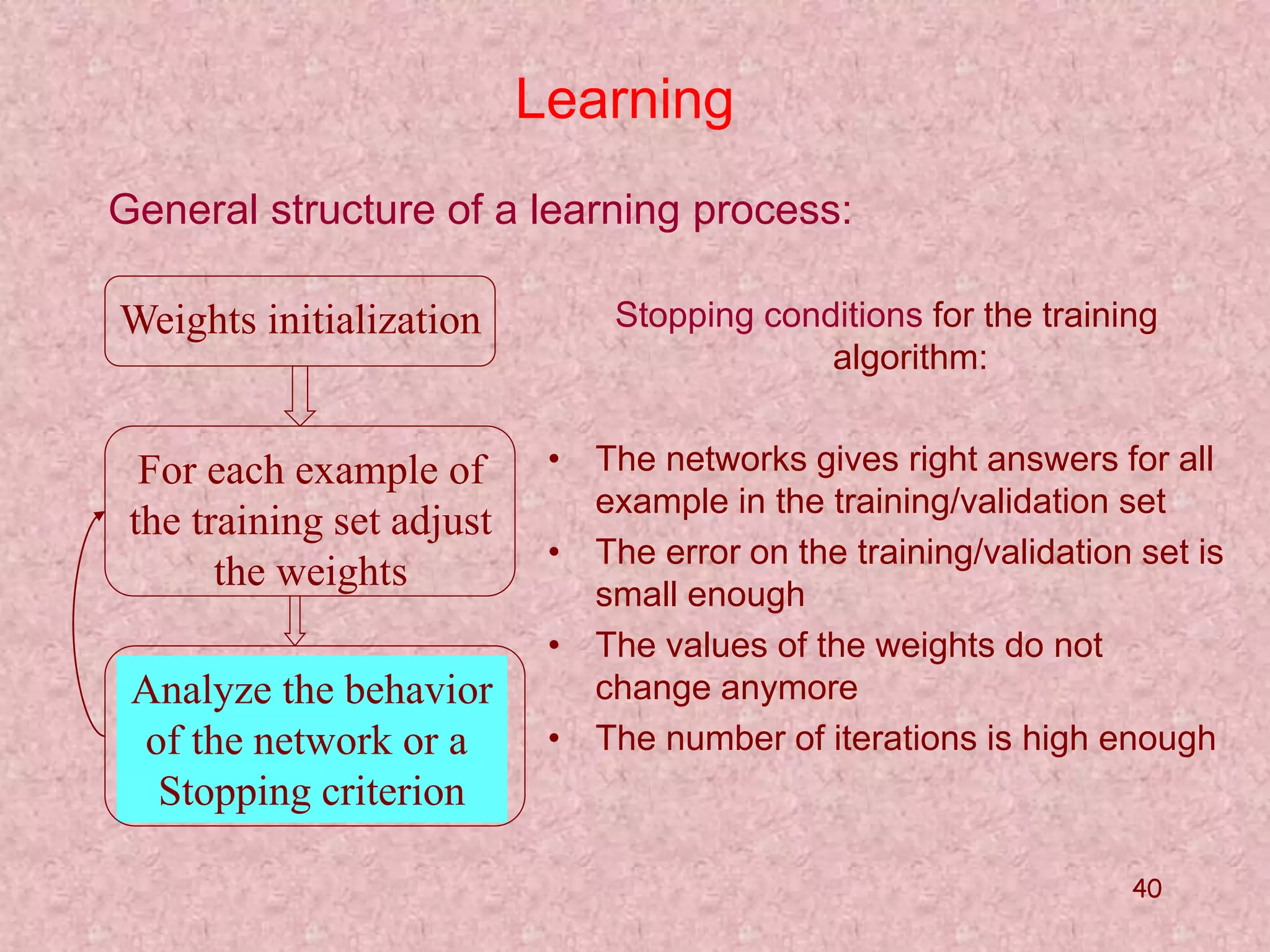
The document discusses soft computing and its techniques, including artificial neural networks (ANN). It provides an overview of ANN, including how biological neurons inspired the basic ANN model. A neuron has inputs, outputs, weights, and an activation function. Networks can be single or multilayer. Learning involves updating weights to minimize error, with backpropagation commonly used for multilayer networks. Applications include pattern recognition, function approximation, and parameter estimation. A simple example is provided to estimate the slope and intercept of a line using ANN.

1. 1
Soft Computing
(ANN & Fuzzy Logic)
Dr. Purnima Pandit
(pkpandit@yahoo.com)
Department of Applied Mathematics
Faculty of Tech. and Engg.
The M.S. University of Baroda

2. What is soft computing ?
Techniques used in soft
computing?

3. What is Soft Computing ?
(adapted from L.A. Zadeh)
• Soft computing differs from
conventional (hard) computing in that,
unlike hard computing, it is tolerant
of imprecision, uncertainty, partial
truth, and approximation. In effect,
the role model for soft computing is
the human mind.

4. What is Hard Computing?
• Hard computing, i.e., conventional
computing, requires a precisely stated
analytical model and often a lot of
computation time.
• Many analytical models are valid for ideal
cases.
• Real world problems exist in a non-ideal
environment.

5. Techniques of Soft Computing
• The principal constituents, i.e., tools,
techniques, of Soft Computing (SC) are
– Fuzzy Logic (FL), Neural Networks (NN),
Support Vector Machines (SVM),
Evolutionary Computation (EC), and
– Machine Learning (ML) and Probabilistic
Reasoning (PR)

6. Premises of Soft Computing
• The real world problems are
pervasively imprecise and uncertain
• Precision and certainty carry a cost

7. Guiding Principles of Soft
Computing
• The guiding principle of soft computing
is:
– Exploit the tolerance for imprecision,
uncertainty, partial truth, and
approximation to achieve tractability,
robustness and low solution cost.

8. Hard Computing
• Premises and guiding principles of Hard
Computing are
– Precision, Certainty, and rigor.
• Many contemporary problems do not lend
themselves to precise solutions such as
– Recognition problems (handwriting,
speech, objects, images)
– Mobile robot coordination, forecasting,
combinatorial problems etc.

9. Implications of Soft Computing
• Soft computing employs NN, SVM, FL etc, in a
complementary rather than a competitive way.
• One example of a particularly effective
combination is what has come to be known as
"neurofuzzy systems.”
• Such systems are becoming increasingly visible
as consumer products ranging from air
conditioners and washing machines to
photocopiers, camcorders and many industrial
applications.

10. Unique Property of Soft computing
• Learning from experimental data
• Soft computing techniques derive their
power of generalization from
approximating or interpolating to
produce outputs from previously unseen
inputs by using outputs from previous
learned inputs
• Generalization is usually done in a high
dimensional space.

11. Current Applications using Soft
Computing
• Application of soft computing to handwriting recognition
• Application of soft computing to automotive systems
and manufacturing
• Application of soft computing to image processing and
data compression
• Application of soft computing to architecture
• Application of soft computing to decision-support
systems
• Application of soft computing to power systems
• Neurofuzzy systems
• Fuzzy logic control

12. Future of Soft Computing
(adapted from L.A. Zadeh)
• Soft computing is likely to play an especially
important role in science and engineering, but
eventually its influence may extend much
farther.
• Soft computing represents a significant paradigm
shift in the aims of computing
– a shift which reflects the fact that the human
mind, unlike present day computers, possesses a
remarkable ability to store and process
information which is pervasively imprecise,
uncertain and lacking in categorization.

13. Techniques in Soft
Computing
• Neural networks
• Support Vector Machines
• Fuzzy Logic
• Genetic Algorithms in Evolutionary
Computation

14. 14
Artificial Neural Networks
– What are they?
– How do they work?
– Different architecture
– Learning Algorithms
– Application to simple parameter
estimation

15. 15
Fundamentals of Neural Networks:
Basic unit
Neuron / Node /
processing
unit
ANN are biologically
inspired networks emitting
human brain to perform
complex tasks

16. Introduction
• Why ANN
– Some tasks can be done easily (effortlessly)
by humans but are hard by conventional
paradigms on Von Neumann machine with
algorithmic approach
• Pattern recognition (old friends, hand-written
characters)
• Content addressable recall
• Approximate, common sense reasoning (driving,
playing piano, baseball player)
– These tasks are often ill-defined,
experience based, hard to apply logic

17. Introduction
Von Neumann machine
---------------------------------------------------------------------------------------------------
------------------------------------------------------------
• One or a few high speed
(ns) processors with
considerable computing
power
• One or a few shared high
speed buses for
communication
• Sequential memory access
by address
• Problem-solving knowledge
is separated from the
computing component
• Hard to be adaptive
Human Brain
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Large # (1011) of low speed
processors (ms) with limited
computing power
Large # (1015) of low speed
connections
Content addressable recall
(CAM)
Problem-solving knowledge
resides in the connectivity
of neurons
Adaptation by changing the
connectivity

18. 18
Neuron in Human Brain

19. Biological neural activity
– Each neuron has a body, an axon, and many dendrites
• Can be in one of the two states: firing and rest.
• Neuron fires if the total incoming stimulus exceeds the threshold
– Synapse: thin gap between axon of one neuron and
dendrite of another.
• Signal exchange
• Synaptic strength/efficiency

20. An (artificial) neural network has:
– A set of nodes (units, neurons, processing
elements)
• Each node has input and output
• Each node performs a simple computation by its
node function
– Weighted connections between nodes
• Connectivity gives the structure/architecture
of the net
• What can be computed by a NN is primarily
determined by the connections and their
weights
– A very much simplified version of networks of
neurons in animal nerve systems

21. ANN -------------------------------------------------------------------------------------
--------------------------------------------------------------------
• Nodes
– input
– output
– node function
• Connections
– connection
strength
Bio NN
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------
• Cell body
– signal firing mechanism
– from other neurons
– firing frequency
• Synapses
– synaptic strength
• Highly parallel, simple local computation (at neuron level)
achieves global results as emerging property of the interaction (at
network level)
• Pattern directed (meaning of individual nodes only in the context
of a pattern)
• Fault-tolerant/graceful degrading
• Learning/adaptation plays important role.

22. History of NN
• Pitts & McCulloch (1943)
– First mathematical model of biological neurons
– All Boolean operations can be implemented by these
neuron-like nodes (with different threshold and
excitatory/inhibitory connections).
– Competitor to Von Neumann model for general purpose
computing device
– Origin of automata theory.
• Hebb (1949)
– Hebbian rule of learning: increase the connection
strength between neurons i and j whenever both i and j
are activated.
– Or increase the connection strength between nodes i
and j whenever both nodes are simultaneously ON or
OFF.

23. History of NN
• Early booming (50’s – early 60’s)
– Rosenblatt (1958)
• Perceptron: network of threshold
nodes for pattern classification
x1 x2 xn
Perceptron learning rule
• Percenptron convergence theorem:
everything that can be represented by a perceptron
can be learned
– Widow and Hoff (1960, 19062)
• Learning rule based on gradient descent (with
differentiable unit)
– Minsky’s attempt to build a general purpose
machine with Pitts/McCullock units

24. History of NN
• The setback (mid 60’s – late 70’s)
– Serious problems with perceptron model
(Minsky’s book 1969)
• Single layer perceonptrons cannot represent (learn)
simple functions such as XOR
• Multi-layer of non-linear units may have greater
power but there is no learning rule for such nets
• Scaling problem: connection weights may grow
infinitely
– The first two problems overcame by latter
effort in 80’s, but the scaling problem persists
– Death of Rosenblatt (1964)
– Striving of Von Neumann machine and AI

25. History of NN
• Renewed enthusiasm and flourish (80’s –
present)
– New techniques
• Backpropagation learning for multi-layer feed forward nets
(with non-linear, differentiable node functions)
• Thermodynamic models (Hopfield net, Boltzmann machine,
etc.)
• Unsupervised learning
– Impressive application (character recognition,
speech recognition, text-to-speech transformation,
process control, associative memory, etc.)
– Traditional approaches face difficult challenges
– Caution:
• Don’t underestimate difficulties and limitations
• Poses more problems than solutions

26. The development in the field of Neural Network started
with the McCulloch - Pitts (1943) model of neuron
26
O
x1
x2
xn
w1
w2
wn
f(wTx) = f(net)
net
w  1, i 1, 2, i
Potential: can perform as Boolean functions:
AND, OR, NOT, NOR, NAND
Activation
function
i i w x

27. 27
Typical activation functions are:
Bipolar
Continuous
Bipolar
binary
Unipolar
Continuous
Unipolar
binary
1
2
1 exp( )

 net
net
 
1, 0

 



1, 0
sgn( )
net
net
1
 net
1 exp( )
net
1, 0






0, 0
sgn( )
net
net
-1
1
-1
1
0
1
0
1

28. 28
Artificial Neural Networks Architectures:
1. Single layer Feed forward Network :
x O
x1
x2
xn
w
1
2
m
o1
o2
om

29. 29
Limitation of Single layer Feed forward
Network:
Fig 1. OR Fig 2. XOR

30. 30
2. Multilayer Feed forward Network :
x O
x1
x2
xn
w
1
2
m1
o1
om
1
m2
h
w

31. 31
3. Recurrent Network :
I1(t)
x xN() 2x () 1()
x1(t) xNx (t) 2(t)
x2(0)
xN(0)
I2(t)
IN(t)
x1(0)

32. 32
LEARNING :
Knowledge in Artificial Neural
Networks lies in the weights.
Acquiring the knowledge i.e.
learning in NN means updating the
weights so that they act as a smart
Black Box.
This NN learning process may be
under supervision or may be
unsupervised one.

33. Learning
• The procedure that consists in estimating the
parameters of neurons so that the whole network can
perform a specific task
• 2 types of learning
– The supervised learning
– The unsupervised learning
• The Learning process (supervised)
– Present the network a number of inputs and their
corresponding outputs
– See how closely the actual outputs match the desired ones
– Modify the parameters to better approximate the desired
outputs

34. Unsupervised learning
• Idea : group typical input data in function
of resemblance criteria un-known a priori
• Data clustering
• No need of a professor
– The network finds itself the correlations
between the data
– Examples of such networks :
• Kohonen feature maps

35. Supervised learning
• The desired response of the neural
network in function of particular
inputs is well known.
• A “Professor” may provide examples
and teach the neural network how to
fulfill a certain task

36. 36
Learning
General structure of a learning process:
Weights initialization
For each example of
the training set adjust
the weights
Analyze the behavior
of the network or a
stopping criterion
(usually randomly)
(different adjusting rules)
Trained network

37. 37
Learning
General structure of a learning process:
Weights initialization
For each example of
the training set adjust
the weights
Analyze the behavior
of the network or a
Stopping criterion
Supervised learning:
Training set: set of pairs
(input data, correct output)
Adjusting rule:
wij(new)=wij(old)+h(yj,xi,eij)
eij - error signal corresponding to weight wij
Usually is based on minimizing an error
function on the training set (the error
function measures how far are the network
answers from the correct ones)

38. 38
Learning
General structure of a learning process:
Weights initialization
For each example of
the training set adjust
the weights
Analyze the behavior
of the network or a
Stopping criterion
Unsupervised learning:
Training set: set of pairs
(input data)
Adjusting rule:
wij(new) = wij(old) + h(yj,xi,)
The adjustment is based only in the
correlation between the input (output)
signals of the corresponding neurons

39. 39
Learning
General structure of a learning process:
Weights initialization
For each example of
the training set adjust
the weights
Analyze the behavior
of the network or a
Stopping criterion
The network behavior can be measured
by using an error function which
expresses the difference between the
desired answers and the answers given
by the network
The error measure can be computed by
using:
• The training set (also used in adjusting
the weights)
• The validation set (not used in
adjusting the weights); measures the
generalization capacity

40. 40
Learning
General structure of a learning process:
Weights initialization
For each example of
the training set adjust
the weights
Analyze the behavior
of the network or a
Stopping criterion
Stopping conditions for the training
algorithm:
• The networks gives right answers for all
example in the training/validation set
• The error on the training/validation set is
small enough
• The values of the weights do not
change anymore
• The number of iterations is high enough

41. 41
Among the different learning
rules the Back
propagation Algorithm for
the multi layer Feed Forward
NN uses the Delta Rule for
the weight updating.

42. 42
Applications of ANN :
• Pattern Association
• Pattern recognition
• Filtering
• Memory
• Function Approximation
•Parameter Estimation

43. 43
Neural Networks
• How do they work?
– The network is trained with a set of
known facts that cover the solution
space (I/O pairs)
• During the training the weights in the
network are adjusted until the correct
answer is given for all the facts in the
training set
– After training, the weights are fixed
and the network answers questions not in
the training data.
• These “answers” are consistent with the
training data

44. 44
Neural Networks
• Concurrent NNs accept all inputs at
once
• Recurrent or dynamic NNs accept
input sequentially and may have one or
more outputs fed back to input
• We consider only concurrent NNs

45. 45
MATLAB® NN Toolbox
• Facilitates easy construction, training
and use of NNs
– Concurrent and recurrent networks
– Linear, tansig, and logsig activation
functions
– Variety of training algorithms
• Backpropagation
• Descent methods (CG, Steepest Descent…)

46. 46
Simple Parameter Estimation
Y = mx+b
• Given a number of points on a line,
determine the slope (m) and intercept
(b) of the line
– Fix number of points at 6
– Restrict domain 0 ≤ x ≤ 1
– Restrict range of b and m to [ -1, 1 ]

47. 47
Simple Example
Approach:
• let the six values of x be fixed at 0,
0.2, 0.4, 0.6, 0.8, and 1.0
• Inputs to the network will be the six
values of y corresponding to these
• Outputs of the network will be the
slope m and intercept b

48. 48
Simple Example

49. 49
Simple Example
%Training data
clear
x = 0:.2:1
par = rand(2,20)
y = zeros(6,20)
for i = 1:20
for j = 1:6
y(j,i) = par(1,i)*x(j)+par(2,i);
end
end
– 20 columns of 6 rows of y data

50. 50
Parameter estimation:
%Training data
– 6 columns of 6 rows of y data
- Corresponding parameter values

51. 51
Parameter estimation:
Neural Network
– 6 inputs – linear activation function
– 10 neurons in hidden layer
• Use tansig activation function
– 2 outputs – tansig activation function
– trained until MSE < 10-6

52. 52
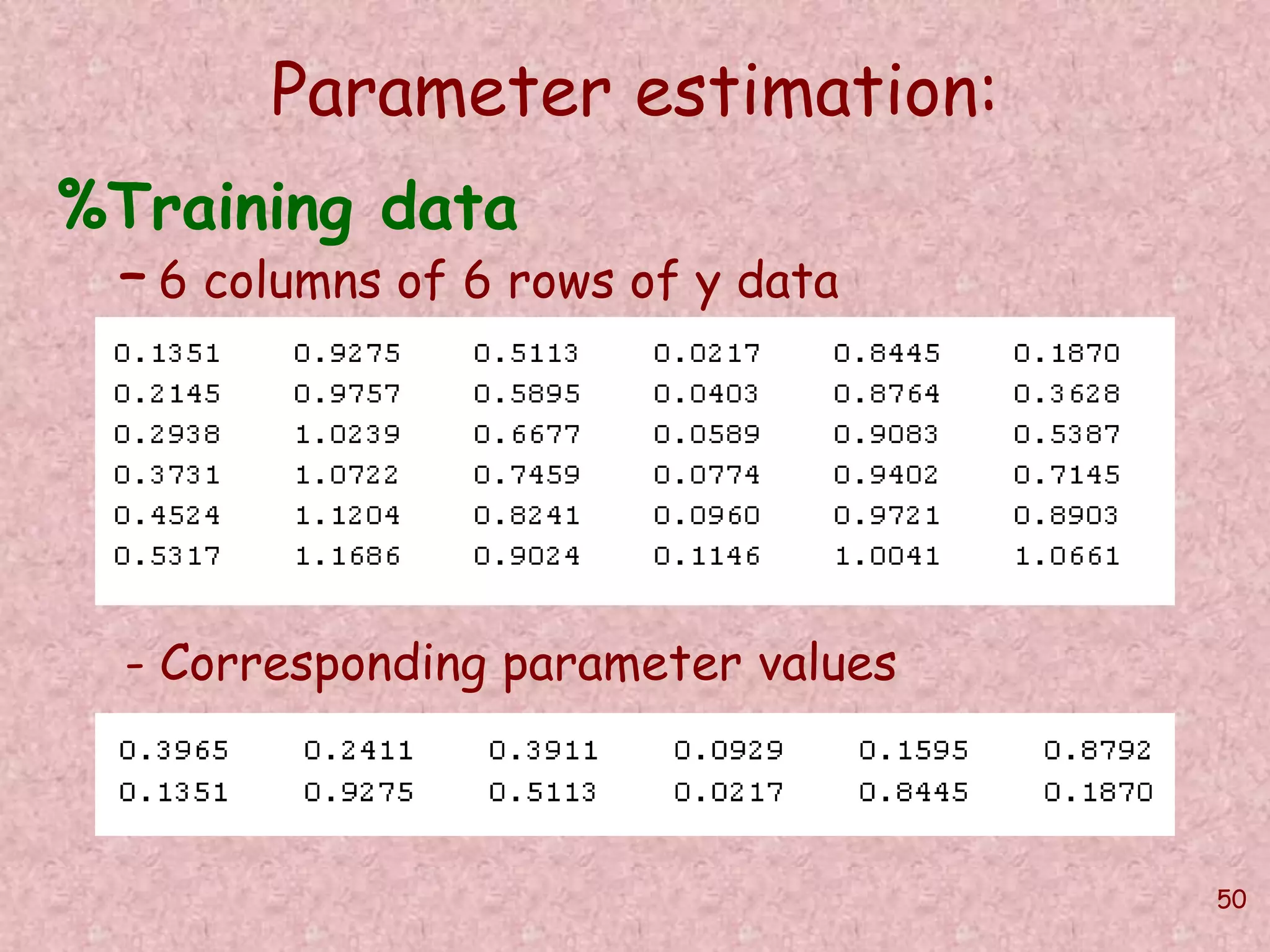
Parameter estimation:
netu = newff([0 1;0 1;0 1;0 1;0 1; 0 1],[10,
2],{'tansig' 'tansig'}, 'trainlm', 'learngdm',
'mse');
netu = init(netu);
Pu = y;
Tu = par;
netu.trainParam.epochs = 100000;
netu.trainParam.goal = 0.000001;
netu = train(netu,Pu,Tu);
yu = sim(netu,Pu)

53. 53
Parameter estimation:

54. 54
Parameter estimation:
Simulation results:
Values used for training:
Values obtained from network:

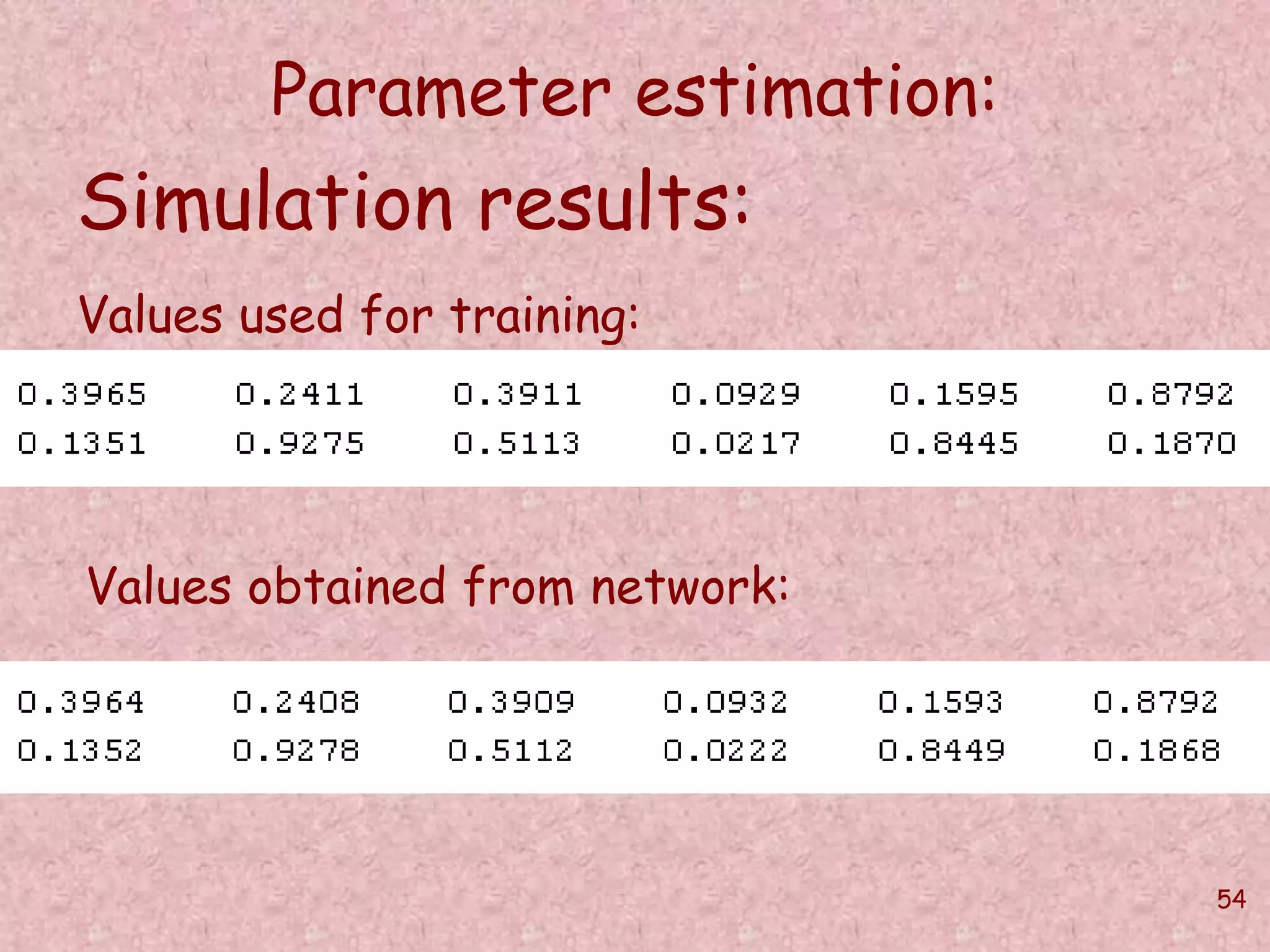
55. 55
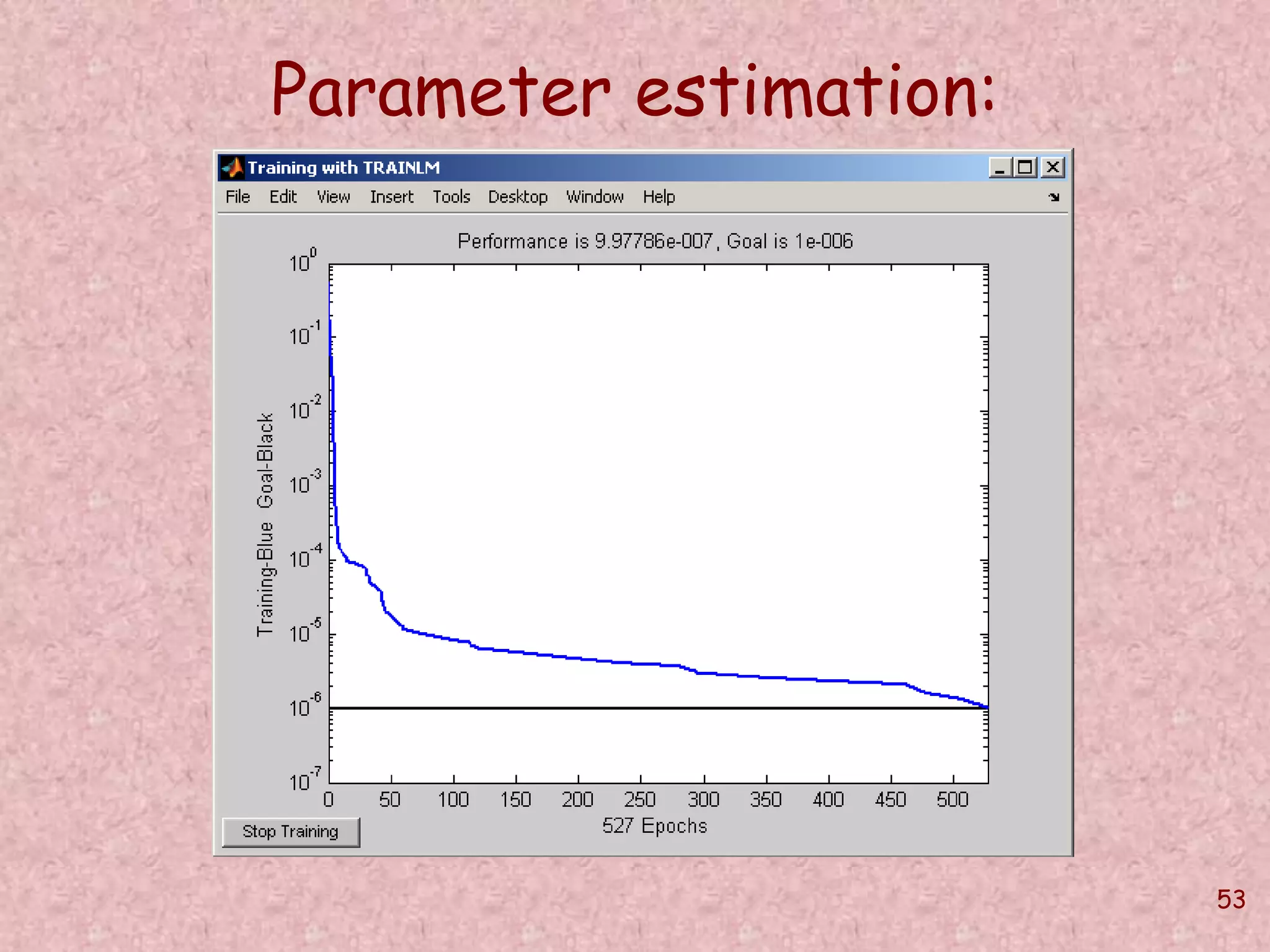
Parameter estimation:
Generalization validation:
Using parameter values
m = 0.3974 and b = 0.7316
we generate input vector:
[ 0.7316 0.8110 0.8905 0.9700 1.0495 1.1290 ]’
For this input vector the trained Neural Network
produces the output as:
0.3946
0.7323

56. 56
Network Design
• First add more neurons in each
layer
• Add more hidden layers if
necessary

57. 57
Neural Networks - Conclusions
• NNs offer possibility of solution of
parameter estimation
• Proper design of the network and
training set is essential for
successful application

58. Instructional Worshop on MATLAB 11 - 13 Dec, 2007
58
FUZZY Toolbox
(MATLAB®)

59. 59
Overview
• Fuzzy Sets
• Fuzzy Logic
• How is Fuzzy Logic used?
• General Fuzzified Applications
• Expert Fuzzified Systems
• An Example
• MATLAB ® Toolbox

60. Introduction
• In 1965* Zadeh published his seminal work
"Fuzzy Sets" which described the mathematics
of Fuzzy Set Theory.
• FST has numbers of applications in various
fields- artificial intelligence, automata theory,
computer science, control theory, decision
making, finance etc.
• It is being applied on a major scale in
industries for machine-building (cars, engines,
ships, etc.) through intelligent robots and
controls.
*L. A. ZADEH, Fuzzy Sets, Information Control, 1965, 8, 338-353.

61. Lotfi A. Zadeh

62. Fuzzy Set Theory deals with the uncertainty and
fuzziness arising from interrelated humanistic types of
phenomena:
Subjectivity
Thinking
Reasoning
Cognition
Perception

63. This approach provides a way to translate a linguistic
model of the human thinking process into a mathematical
framework for developing the computer algorithms for
computerized decision-making processes.
crisp
fuzzy
very cold

64. In general, fuzziness describes
objects or processes that are not
acquiescent to precise definition or
precise measurement. Thus, fuzzy
processes can be defined as processes
that are vaguely defined and have some
uncertainty in their description. The
data arising from fuzzy systems are in
general, soft, with no precise
boundaries.

65. Fuzziness in Everyday World
John is tall;
Temperature is hot;
The girl next door is pretty;
The sun is getting relatively hot;
The people living close to Vadodara;
My car is slow, your car is fast;

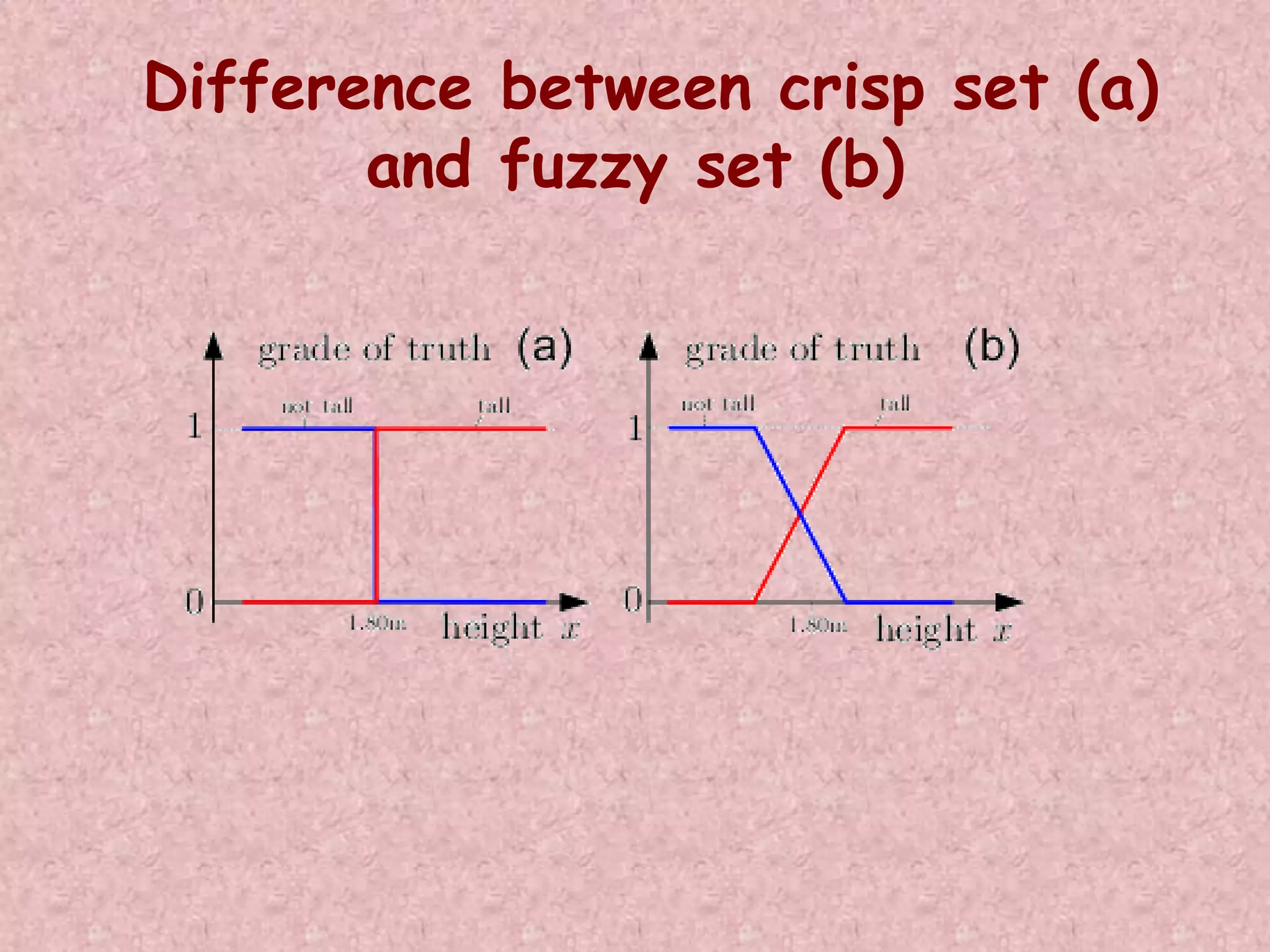
66. Characteristic Function in the Case
of Crisp Sets and Fuzzy Sets
P: X  {0,1}
P(x) =
A : X  [0,1]
A = {X, A(x)} if x  X
1 if



x X

x 
X
0 if
A Fuzzy Set is a generalized set to which objects can
belongs with various degrees (grades) of memberships
over the interval [0,1].

67. Difference between crisp set (a)
and fuzzy set (b)

68. Operations on Fuzzy sets
• Standard complement :-
A’(x) = 1 − A(x)
• Standard intersection:-
(A ∩ B)(x) = min [A(x), B(x)]
• Standard union:-
(A U B)(x) = max [A(x), B(x)]

69. 69
Fuzzy Logic – A Definition
Fuzzy logic provides a method to formalize reasoning when
dealing with vague terms.
Traditional computing requires finite precision which is not
always possible in real world scenarios.
Not every decision is either true or false, or as with
Boolean logic either 0 or 1.
Fuzzy logic allows for membership functions, or degrees of
truthfulness and falsehoods.
Or as with Boolean logic, not only 0 and 1 but all the
numbers that fall in between.

70. 70
How is Fuzzy Logic Used?
Fuzzy Mathematics
Fuzzy Numbers – almost 5, or more
than 50
Fuzzy Geometry – Almost Straight
Lines
Fuzzy Algebra – Not quite a
parabola
Fuzzy graphs – based on fuzzy
points

71. 71
General Fuzzified Applications
• Quality Assurance
• Error Diagnostics
• Control Theory
• Pattern Recognition

72. 72
Expert Fuzzified Systems
• Medical Diagnosis
• Legal
• Stock Market Analysis
• Mineral Prospecting
• Weather Forecasting
• Economics
• Politics

73. 73
MATLAB® Fuzzy Toolbox
newfis - Create new FIS.
FIS=NEWFIS(FISNAME) creates a new
Mamdani-style FIS structure
FIS=NEWFIS(FISNAME, FISTYPE) creates a
FIS structure for a Mamdani or Sugeno-style
system with the name FISNAME.

74. 74
MATLAB® Fuzzy Toolbox
Illustration : Fuzzy Washing Machine
Depending on two fuzzy inputs dirt and
type of dirt the fuzzy inference system
calculates the wash time.
w = newfis('Wash');

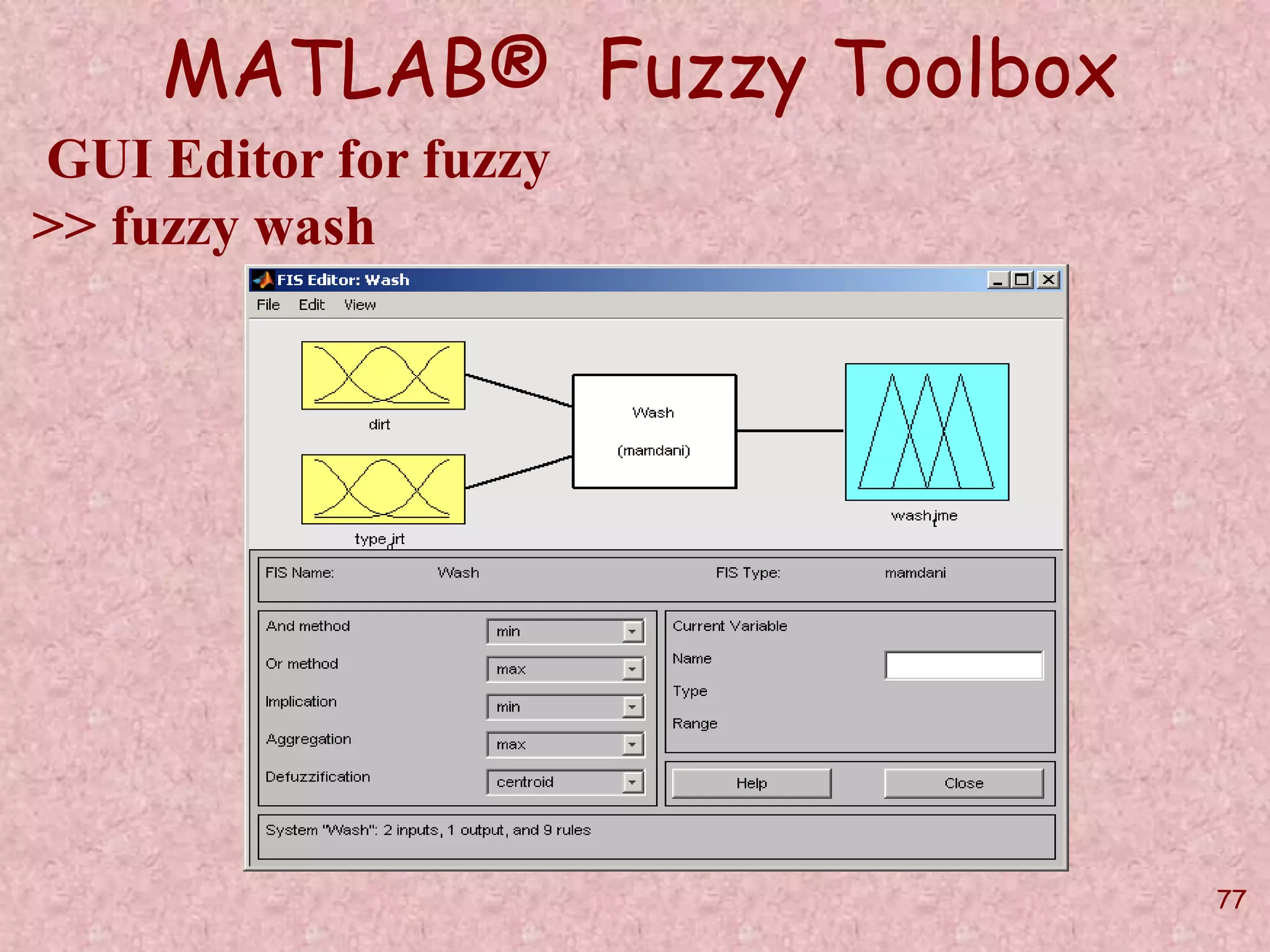
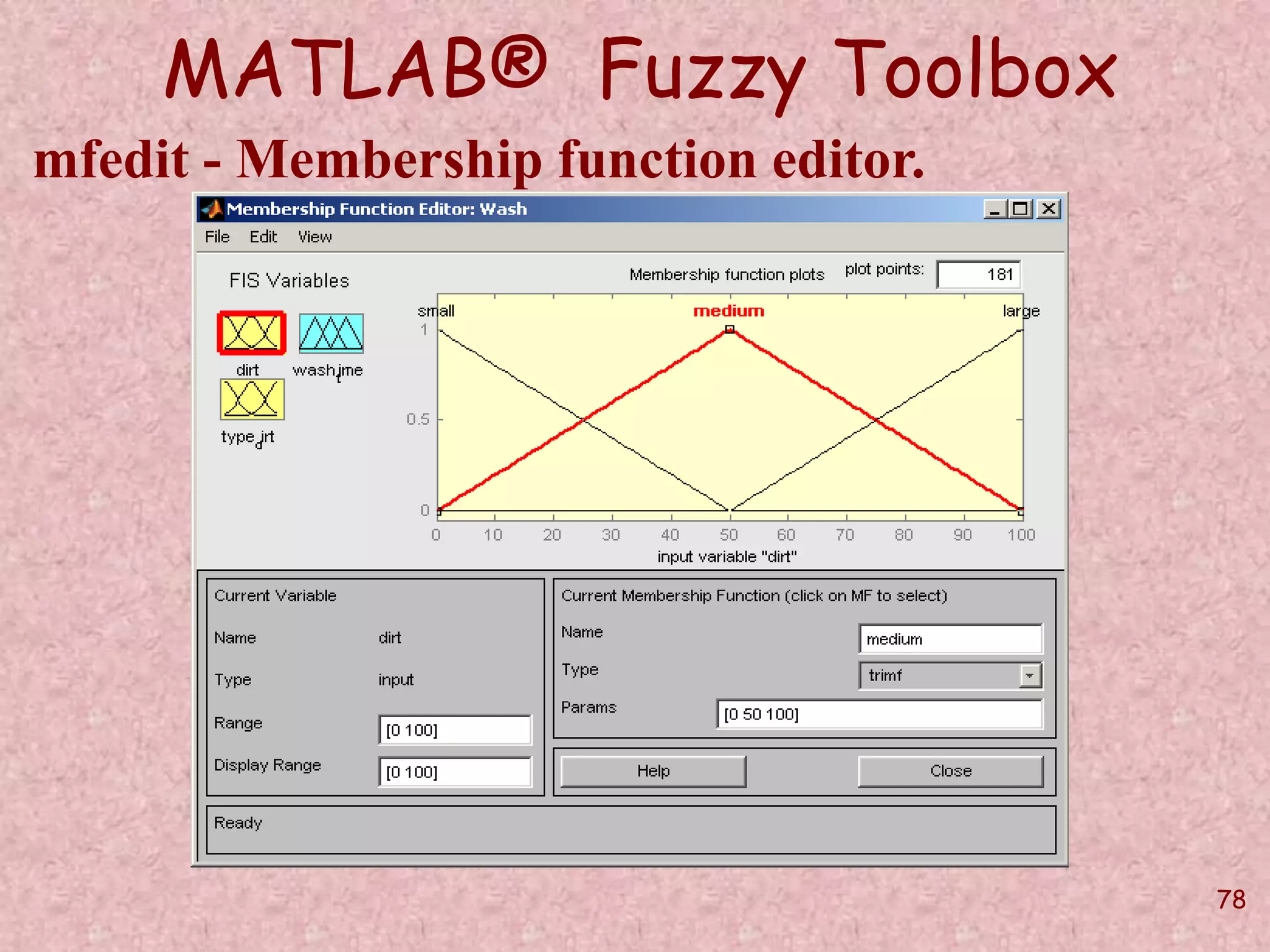
75. 75
MATLAB® Fuzzy Toolbox
addvar - Add variable to FIS.
w = addvar(w,varType,varName,varBounds)
w = addvar(w,'input','dirt',[0,100]);
addmf - Add membership function to FIS
w = addmf(w,varType,varIndex,mfName,
mfType, mfParams)
w = addmf(w,'input',1,'small','trimf',[-50 0 50]);

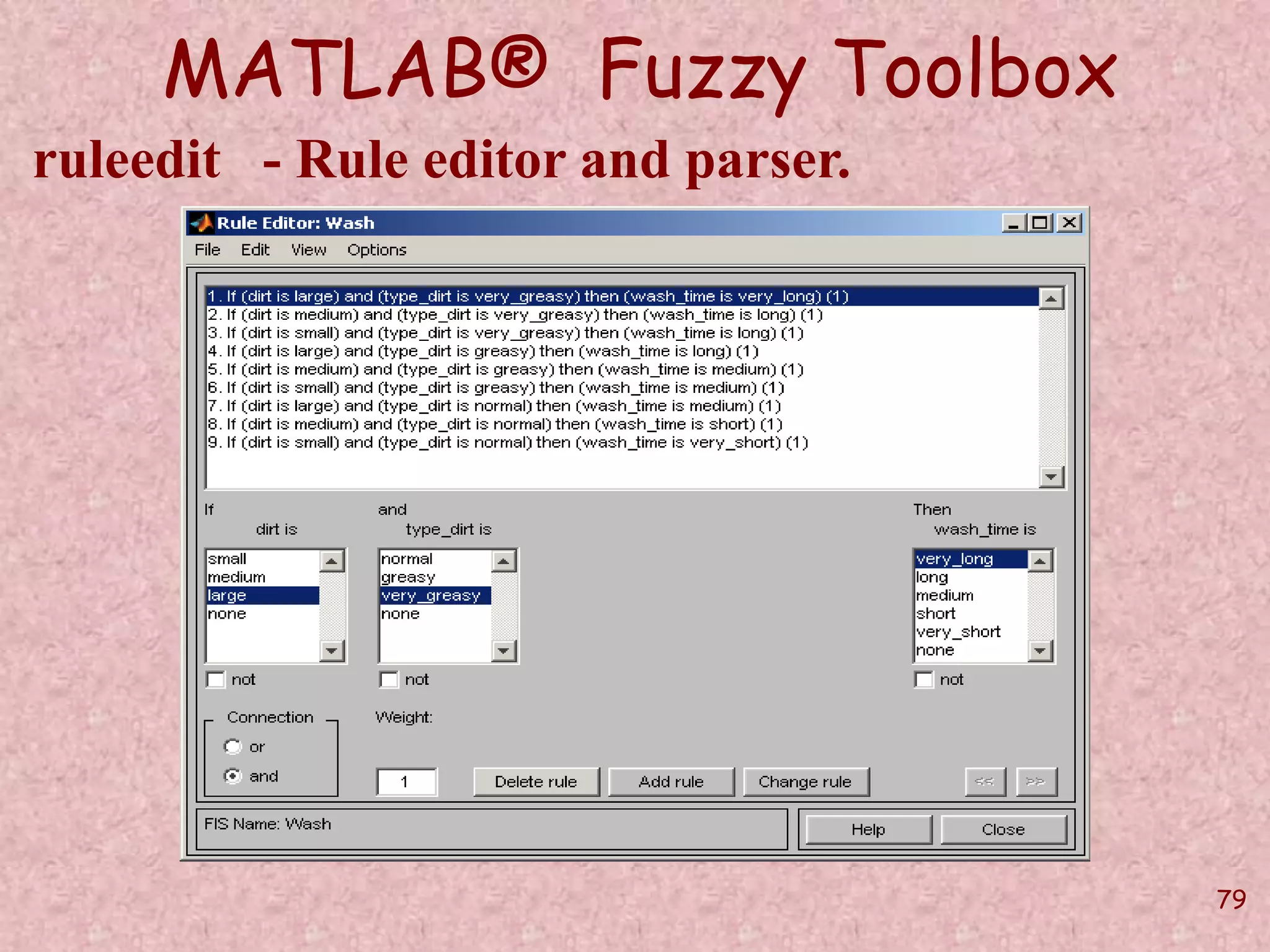
76. 76
MATLAB® Fuzzy Toolbox
addrule - Add rule to FIS.
ruleList=[1 1 1 1 1;
1 2 2 1 1];
w = addrule(w,ruleList);

77. 77
MATLAB® Fuzzy Toolbox
GUI Editor for fuzzy
>> fuzzy wash

78. 78
MATLAB® Fuzzy Toolbox
mfedit - Membership function editor.

79. 79
MATLAB® Fuzzy Toolbox
ruleedit - Rule editor and parser.

80. 80
MATLAB® Fuzzy Toolbox
ruleview - Rule viewer and fuzzy inference
diagram.

81. 81
MATLAB® Fuzzy Toolbox
surfview - Output surface viewer.

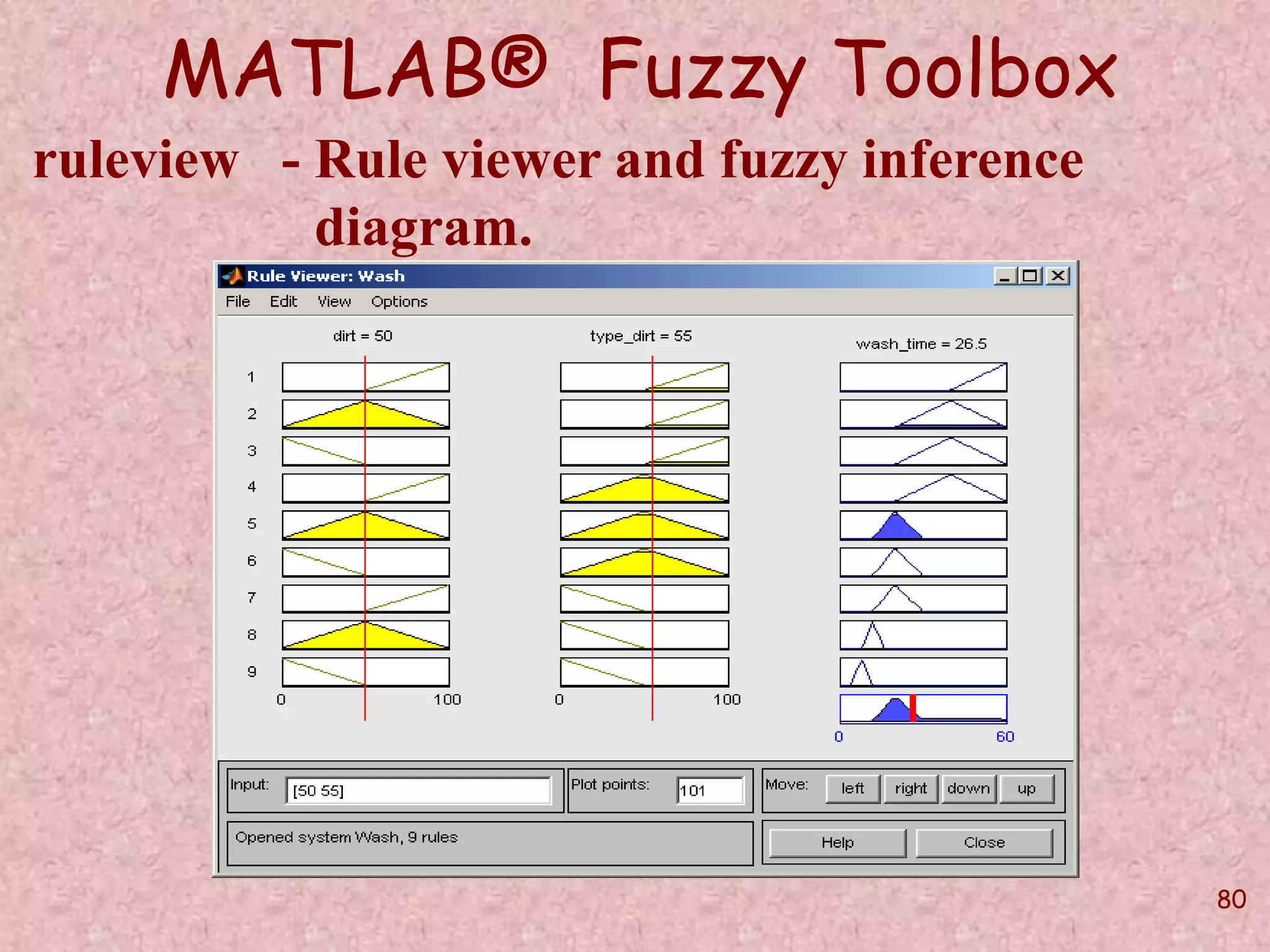
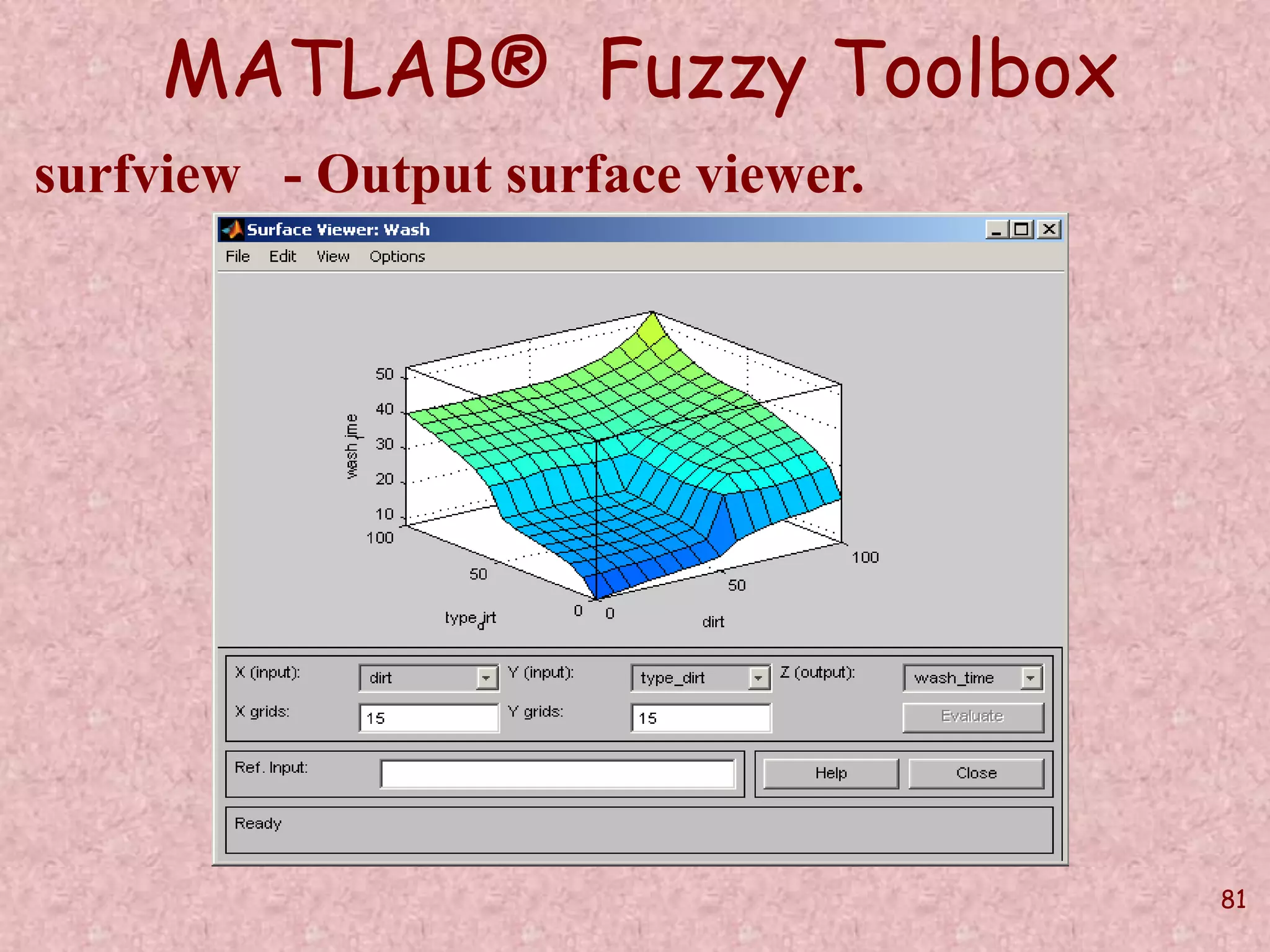
82. 82
MATLAB® Fuzzy Toolbox
w = newfis('Wash');
w = addvar(w,'input','dirt',[0,100]);
w = addvar(w,'input','type_dirt',[0,100]);
w = addvar(w,'output','wash_time',[0,60]);
w = addmf(w,'input',1,'small','trimf',[-50 0 50]);
w = addmf(w,'input',1,'medium','trimf',[0 50 100]);
w = addmf(w,'input',1,'large','trimf',[50 100 150]);
w = addmf(w,'input',2,'normal','trimf',[-50 0 50]);
w = addmf(w,'input',2,'greasy','trimf',[0 50 100]);
w = addmf(w,'input',2,'very_greasy','trimf',[50 100 150]);
w = addmf(w,'output',1,'very_long','trimf',[40 60 80]);
w = addmf(w,'output',1,'long','trimf',[20 40 60]);
w = addmf(w,'output',1,'medium','trimf',[12 20 30]);
w = addmf(w,'output',1,'short','trimf',[8 12 16]);
w = addmf(w,'output',1,'very_short','trimf',[4 8 12]);
ruleList = [3 3 1 1 1;2 3 2 1 1; 1 3 2 1 1; 3 2 2 1 1; 2 2 3 1 1; 1 2 3 1 1; 3 1 3 1 1;2 1 4 1 1;
1 1 5 1 1];
w = addrule(w,ruleList);
gensurf(w,[1 2]);
surfview(w)

83. 83
Happy Fuzzyfying
with MATLAB
for any of the following:
• Hair Dryers
• Cranes
• Electric Razors
• Camcorders
• Television Sets
• Showers
• Pen

84. 84
ALL THE BEST
HAVE A GREAT
SUCCESS
WITH
Soft Computing ANN, FL
and MATLAB