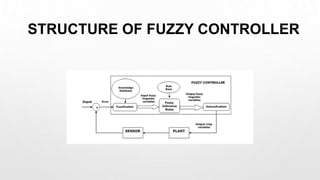
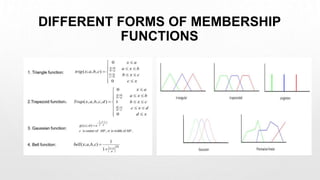
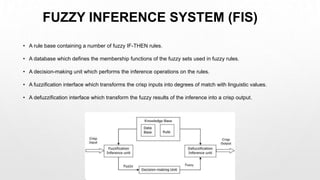
This document outlines the design procedure for a fuzzy controller, including its key components and their functions. It discusses fuzzification, membership functions, a knowledge base containing fuzzy rules, a fuzzy inference system for mapping inputs to outputs, and defuzzification to produce a crisp output. An example of a temperature control system is provided to illustrate these concepts. Fuzzy controllers are widely used in applications like process control due to their ability to handle imprecise and uncertain data through human-like reasoning.

1. Name Ammar Muhammad
Subject Intelligent Control Application
Topic Fuzzy Controller Design Procedure
Professor Chan Zhou

2. CONTENTS
• What is Fuzzy Controller?
• Structure of Fuzzy Controller
• Importance in Control Systems
• Example problem: Temperature Control
• Fuzzification
• Membership Functions And Linguistic Variables
• Knowledge base (Rule Set)
• Fuzzy inference system (FIS)
• Defuzzification in Fuzzy Logic
• Summary

3. WHAT IS FUZZY CONTROLLER?
• A fuzzy controller is a type of control system that uses linguistic variables to emulates human decision-making
in handling uncertain or imprecise information to handle complex and non-linear control systems.
• It employs fuzzy logic to interpret input variables, assess them against a set of rules, and produce continuous
output values.
• This controller operates by creating relationships between input and output using fuzzy sets, membership
functions, and rule-based reasoning, making it well-suited for systems where traditional binary control isn't
precise enough.
• This intelligent control system is widely used in various applications, such as robotics, process control, and
automation.

4. STRUCTURE OF FUZZY CONTROLLER

5. IMPORTANCE IN CONTROL SYSTEMS
1. Handling uncertainty: Traditional control systems often struggle with handling uncertain or imprecise information. Fuzzy logic excels here by
allowing for imprecise inputs and linguistic descriptions, enabling effective decision-making even with incomplete or vague data.
2. Human-like reasoning: it mimics human decision-making processes by allowing for linguistic variables and rules. This flexibility enables
controllers to be more natural, making it easier to incorporate expert knowledge into the control system.
3. Robustness: fuzzy control systems tend to be more robust in dealing with dynamic or nonlinear systems. They adapt well to changing
environments or system conditions, providing stability and improved performance.
4. Complex system control: fuzzy logic enables control over systems that are difficult to model precisely. It's particularly useful in systems where
mathematical modeling is challenging or where the system behavior is highly nonlinear.
5. Simple implementation: fuzzy controllers can often be implemented more straightforwardly compared to complex mathematical models. They
require fewer computations and can be easily understood and implemented in various hardware and software systems.
• Overall, the adaptability, robustness, and ability to handle uncertainty make fuzzy logic a valuable tool in control systems across various
industries and applications.

6. EXAMPLE PROBLEM: TEMPERATURE
CONTROL
Temperature control using fuzzy logic
Scenario: controlling room temperature
Objective: utilizing fuzzy controller for precision
Control variables
Input variable: Temperature Error
• Linguistic terms: cold, warm, hot
• Membership functions: representing fuzzy sets
Output variable: Heater Power
• Linguistic terms: low, medium, high
• Mapping membership functions for control output

7. Nonlinear mapping of an input data set to a scalar output data is known as fuzzy logic system. A fuzzy logic
system consists of four main parts:
• Fuzzifier
• Rules
• Inference engine
• Defuzzifier.
These components and the general architecture of a fuzzy logic system
Example Problem: Temperature Control

8. FUZZIFICATION
• Fuzzification is a process within fuzzy logic that converts crisp, numerical input values into fuzzy sets or
linguistic variables.
• In traditional logic or mathematics, inputs are precise and exact, but in real-world scenarios, information might
be imprecise, uncertain, or vague.
• Fuzzy logic addresses this by allowing inputs to be represented not just as precise values, but as linguistic terms
or fuzzy sets that capture degrees of membership.

9. MEMBERSHIP FUNCTIONS AND
LINGUISTIC VARIABLES
Membership function (MF) -
A function which represents
the graph of fuzzy sets that
allows users to quantify the
linguistic term.
Linguistic variables represent
crisp information in a form
and precision appropriate for
the problem.
Degree of membership- the
output of a membership
function, this value is always
limited to between 0 and 1.
Also known as a
membership value or
membership grade.
Each linguistic term covers a
relatively wide range of
numerical values. Its value is
not a number but word.

10. DIFFERENT FORMS OF MEMBERSHIP
FUNCTIONS

11. KNOWLEDGE BASE (RULE SET)
• Most of the fuzzy logic applications involve construction and processing of fuzzy rules.
• Fuzzy rules serve to describe, in linguistic terms, a qualitative relationship between two or more variables.
• In a fuzzy logic, a rule base is constructed to control the output variable.
• A fuzzy logic controller describes a control protocol by means of IF-THEN rules, such as "IF temperature is
low open heating valve slightly".

12. RULE BASE CREATION IN FUZZY LOGIC
• IF-THEN rules for decision making
Example rule: IF temperature is cold THEN heater power is high
Linguistic variables linked via IF-THEN statements
Explanation of rules reflecting control actions
• Components of rule base
Linguistic variables interconnection:
Temperature error ↔ heater power
Multiple IF-THEN statements for different scenarios

13. RULE BASE CREATION IN FUZZY LOGIC(CONT.)
• Rule base importance: forms core decision-making structure
• Human-like reasoning: allows incorporation of expert knowledge
• Flexibility: adaptable to varying control scenarios
• The concept of rule base creation in fuzzy logic, emphasizing the structure of IF-THEN rules connecting linguistic
variables and explaining their importance in decision-making within a fuzzy controller.
• The visual representation will aid in demonstrating how linguistic variables are interconnected to determine control
actions.

14. FUZZY INFERENCE SYSTEM (FIS)
• A rule base containing a number of fuzzy IF-THEN rules.
• A database which defines the membership functions of the fuzzy sets used in fuzzy rules.
• A decision-making unit which performs the inference operations on the rules.
• A fuzzification interface which transforms the crisp inputs into degrees of match with linguistic values.
• A defuzzification interface which transform the fuzzy results of the inference into a crisp output.

15. FIS (CONTINUED)
• Fuzzy operators: logical operations in fuzzy logic
Types of fuzzy operators
1. AND operator (t-norm):
1. Purpose: represents intersection
2. Example: MIN operator - t-norm representing minimum membership
2. OR operator (t-conorm):
1. Purpose: represents union
2. Example: MAX operator - t-conorm representing maximum membership
3. NOT operator:
1. Purpose: represents complement
2. Example: 1 - membership degree

16. CONT.
• DEGREE OF RELATIONSHIP:
Define degrees of membership or relationship in rules (e.g., High, low, very high)
• Fuzzy relation matrix
• Illustrate a matrix showing the degrees of relationship between input (temperature error) and output (heater
power) fuzzy sets.
• Rows represent input linguistic terms; columns represent output linguistic terms.
• Highlight how changes in input (e.g, From cold to warm) impact the output (e.G., From high to medium heater
power).
Slow Moderate Fast Very Fast
Slow Very Slow Slow Moderate Fast
Moderate Slow Moderate Fast Very Fast
Fast Moderate Fast Very Fast Very Fast
Very Fast Fast Very Fast Very Fast Very Fast

17. DEFUZZIFICATION IN FUZZY LOGIC
• The procedure of producing a quantitative outcome in fuzzy logic, given fuzzy sets and corresponding
membership degrees can be described as term “Defuzzification”.
• It is basically required in fuzzy control arrangements. These arrangements will contain large number of rules
which will convert a number of variables into a fuzzy result and eventually the converted variables called
results are expressed in terms of membership in fuzzy sets.
• In the defuzzification the methods (centroid and max membership), and their significance in obtaining crisp
outputs from fuzzy set outputs.
• Emphasizing the importance of this process in finalizing control actions and the consideration of method
selection based on application requirements.

18. SUMMARY
• Fuzzy controller design procedure
• Defined linguistic variables & fuzzy sets
• Created rule base & fuzzy inference mechanism
• Determined fuzzy relation & Defuzzified output
• Applications
• Widespread use: HVAC systems, robotics, traffic control
• Enhanced control: better performance in dynamic environments
• Fuzzy valuable in complex control systems
• The conclusion emphasizes the importance of fuzzy logic in addressing complex control challenges and its
continuous evolution to meet dynamic system demands.

19. REFERENCE
• BOOK OF FUZZY CONTROL KEVIN M. PASSINO DEPARTMENT OF ELECTRICAL ENGINEERING THE OHIO STATE UNIVERSITY.
• BOOK FUZZY CONTROLLERS LEONID REZNIK VICTORIA UNIVERSITY OF TECHNOLOGY, MELBOURNE, AUSTRALIA
• A. HAMAM AND N. D. GEORGANAS, “A COMPARISON OF MAMDANI AND SUGENO FUZZY INFERENCE SYSTEMS FOR EVALUATING THE QUALITY OF
EXPERIENCE OF HAPTO-AUDIO-VISUAL APPLICATIONS” HAVE 2008 – IEEE INTERNATIONAL WORKSHOP ON HAPTIC AUDIO VISUAL ENVIRONMENTS AND
THEIR APPLICATIONSOTTAWA CANADA, 18-19 OCTOBER 2008.
• RAJANI K. MUDI AND NIKHIL R. PAL, “A NOTE ON FUZZY PI-TYPE CONTROLLERS WITH RESETTING ACTION”, ELSEVIER, FUZZY SETS AND SYSTEMS 121
(2001) 149–159.
• RAJANI K. MUDI AND NIKHIL R. PAL, “A ROBUST SELF-TUNING SCHEME FOR PI- AND PD-TYPE FUZZY CONTROLLERS” IEEE HILL, G., HORSTKOTTE, E. AND
TEICHROW, J. (1990). )X]]& GHYHORSPHQW VVWHP ± XVHUV PDQXDO , TOGAI INFRALOGIC, 30 CORPORATE PARK, IRVINE, CA 92714, USA.
• HOLMBLAD, L. P. AND ØSTERGAARD, J.-J. (1982). CONTROL OF A CEMENT KILN BY FUZZY LOGIC, LQ GUPTA AND SANCHEZ (EDS), )X]] ,QIRUPDWLRQ DQG
'HFLVLRQ 3URFHVVHV, NORTH-HOLLAND, AMSTERDAM, PP. 389–399. (REPRINT IN: FLS REVIEW NO 67, FLS AUTOMATION A/S, HØFFDINGSVEJ 77, DK-
2500 VALBY, COPENHAGEN, DENMARK).