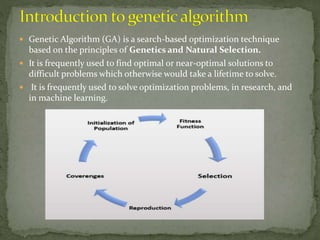
The document provides an overview of fuzzy set theory and its operations, distinguishing between crisp sets and fuzzy sets, and detailing their properties, including membership functions and fuzzy rules. It also introduces genetic algorithms as a search-based optimization technique, discussing their advantages, such as efficiency and parallel capabilities, alongside their limitations. Key concepts include fuzzy reasoning, inference systems (Mamdani and Sugeno), and the compositional rule of inference.

1. Present by . Absar Qureshi
E.No 0801IT193D01
Subject: Artificial Intelligence

2.  Introduction
 Differences between crisp sets & Fuzzy sets
 Operations on Fuzzy Sets
 Properties
 MF formulation and parameterization
 Fuzzy rules and Fuzzy reasoning
 Fuzzy interface systems
 Introduction to genetic algorithm

3.  Fuzzy sets have been introduced by Zadeh 1965.
 Fuzzy Sets: Those collection of objects where it is not
possible to make a sharp distinction between the
belongingness or non-belongingness to the collection.
 These are useful in cases where the source of
imprecision is the absence of sharply defined criteria
of the class of membership rather that the probability
theory.

4.  Let the universal set be denoted by X and its elements by x
i.e. X= {x}. We define a set A on X such that 𝐴 ⊂ 𝑋. We
define the term grade of membership denoted by fA(x)
which represents the information regarding the extent of
belongingness of x to set A.
 If 𝑥 ∈ 𝑋, if fA(x)= 0 or 1 only and no intermediate value,
then the set A is called the crisp set and if the value of fA x
belongs to the closed interval [0, 1], then A is called the
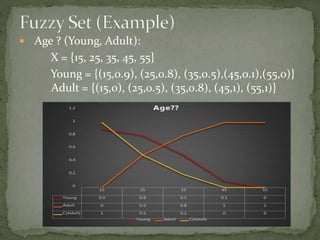
Fuzzy set. Eg: For the set X= set of real numbers close to 1,
we have fA 0 = 0; fA 10 = 0.2; fA 500 = 1

5.  Empty FS: 𝑓𝐴 𝑥 = 0 ∀𝑥 ∈ 𝑋
 Equal FSs:
Given two FSs A & B, then if 𝑓𝐴 𝑥 = 𝑓𝐵(𝑥)∀𝑥 ∈ 𝑋, then A=B
 Complement(𝑨 ′ ):
It is defined as 𝑓𝐴 ′ 𝑥 = 1 − 𝑓𝐴(𝑥)
 Subset:
𝐴 ⊂ 𝐵 ↔ 𝑓𝐴 ≤ 𝑓𝐵 𝑖. 𝑒. 𝑓𝐴 𝑥 ≤ 𝑓𝐵 𝑥 ∀𝑥 ∈ 𝑋
 Union:
Let 𝐶 = 𝐴 ∪ 𝐵,𝑡ℎ𝑒𝑛 𝑓𝑐 𝑥 = 𝑀𝑎𝑥 𝑓𝐴 𝑥 , 𝑓𝐵 𝑥 , ∀𝑥 ∈ 𝑋
Corollary: The union of A & B is the smallest fuzzy set containing both A & B.
 Intersection:
Let 𝐶 = 𝐴 ∩ 𝐵,𝑡ℎ𝑒𝑛 𝑓𝑐 𝑥 = 𝑀𝑖𝑛 𝑓𝐴 𝑥 , 𝑓𝐵 𝑥 , ∀𝑥 ∈ 𝑋
Corollary: The intersection of A & B is the largest fuzzy set containing both A & B.

6.  Age ? (Young, Adult):
X = {15, 25, 35, 45, 55}
Young = {(15,0.9), (25,0.8), (35,0.5),(45,0.1),(55,0)}
Adult = {(15,0), (25,0.5), (35,0.8), (45,1), (55,1)}

7.  Fuzzy set are defined as sets that contain elements having varying degrees
of membership values. Given A and B are two fuzzy sets, here are the main
properties of those fuzzy sets:
 Commutativity :-
(A ∪ B) = (B ∪ A)
(A ∩ B) = (B ∩ A)
 Associativity :-
(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
 Distributivity :-
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
 Idempotent :-
A ∪ A = A
A ∩ A = A

8.  Identity :-
A ∪ Φ = A => A ∪ X = X
A ∩ Φ = Φ => A ∩ X = A
Note: (1) Universal Set ‘X’ has elements with unity membership value.
(2) Null Set ‘Φ’ has all elements with zero membership value.
 Transitivity :-
If A ⊆ B, B ⊆ C, then A ⊆ C
 Involution :-
(Ac)c = A
 De morgan Property :-
(A ∪ B)c = Ac ∩ Bc
(A ∩ B)c = Ac ∪ Bc
 Note: A ∪ Ac ≠ X ; A ∩ Ac ≠ Φ

9. In the following, we try to parameterize the different MFs
on a continuous universe of discourse

10.  Fuzzy rules are used within fuzzy logic systems to
infer an output based on input variables. Modus
ponens and modus tollens are the most important
rules of inference.[1]A modus ponens rule is in the form
 Premise: x is AImplication: IF x is A THEN y is
BConsequent: y is B
 In crisp logic, the premise x is A can only be true or
false. However, in a fuzzy rule, the premise x is A and
the consequent y is B can be true to a degree, instead
of entirely true or entirely false

11.  Fuzzy reasoning, also known as approximate reasoning, is a inference
procedure that derives conclusions from a set of fuzzy if-then rules and
known facts. Before introducing fuzzy reasoning, we shall discuss the
compositional rule of inference, which plays a key role in fuzzy
reasoning.
 The basic rule of inference in traditional two-value topic is modus
ponens , according to which we can infer the truth of a proposition B
from the truth of A and the implication A → B. For instance, if A is
identified with "the tomato is red" and B with "the tomato is ripe," then
if it is true that "the tomato is red," it is also true that "the tomato is
ripe".
 This concept is illustrated as follows:

12.  A fuzzy inference system (FIS) is a system that uses fuzzy set
theory to map inputs (features in the case of fuzzy classification)
to outputs (classes in the case of fuzzy classification). Two FIS�s
will be discussed here, the Mamdani and the Sugeno.
Example of Fuzzy Interface System
 An example of a Mamdani inference system is shown
in figure To compute the output of this FIS given the
inputs, one must go through six steps:
 1. determining a set of fuzzy rules
 2. fuzzifying the inputs using the input membership
functions,

13. 3. combining the fuzzified inputs according to the fuzzy rules to establish a rule
strength,
4. finding the consequence of the rule by combining the rule strength and the
output membership function,
5. combining the consequences to get an output distribution, and
6. defuzzifying the output distribution (this step is only if a crisp output (class) is
needed)
Example of Fuzzy Interface System

14.  Genetic Algorithm (GA) is a search-based optimization technique
based on the principles of Genetics and Natural Selection.
 It is frequently used to find optimal or near-optimal solutions to
difficult problems which otherwise would take a lifetime to solve.
 It is frequently used to solve optimization problems, in research, and
in machine learning.

15. GAs have various advantages which have made them immensely popular.
These include −
 Does not require any derivative information (which may not be available for
many real-world problems).
 Is faster and more efficient as compared to the traditional methods.
 Has very good parallel capabilities.
 Optimizes both continuous and discrete functions and also multi-objective
problems.
 Provides a list of “good” solutions and not just a single solution.
Limitations of GAs
Like any technique, GAs also suffer from a few limitations. These include −
 GAs are not suited for all problems, especially problems which are
simple and for which derivative information is available.
 Fitness value is calculated repeatedly which might be computationally
expensive for some problems.
 Being stochastic, there are no guarantees on the optimality or the quality
of the solution.
 If not implemented properly, the GA may not converge to the optimal
solution.