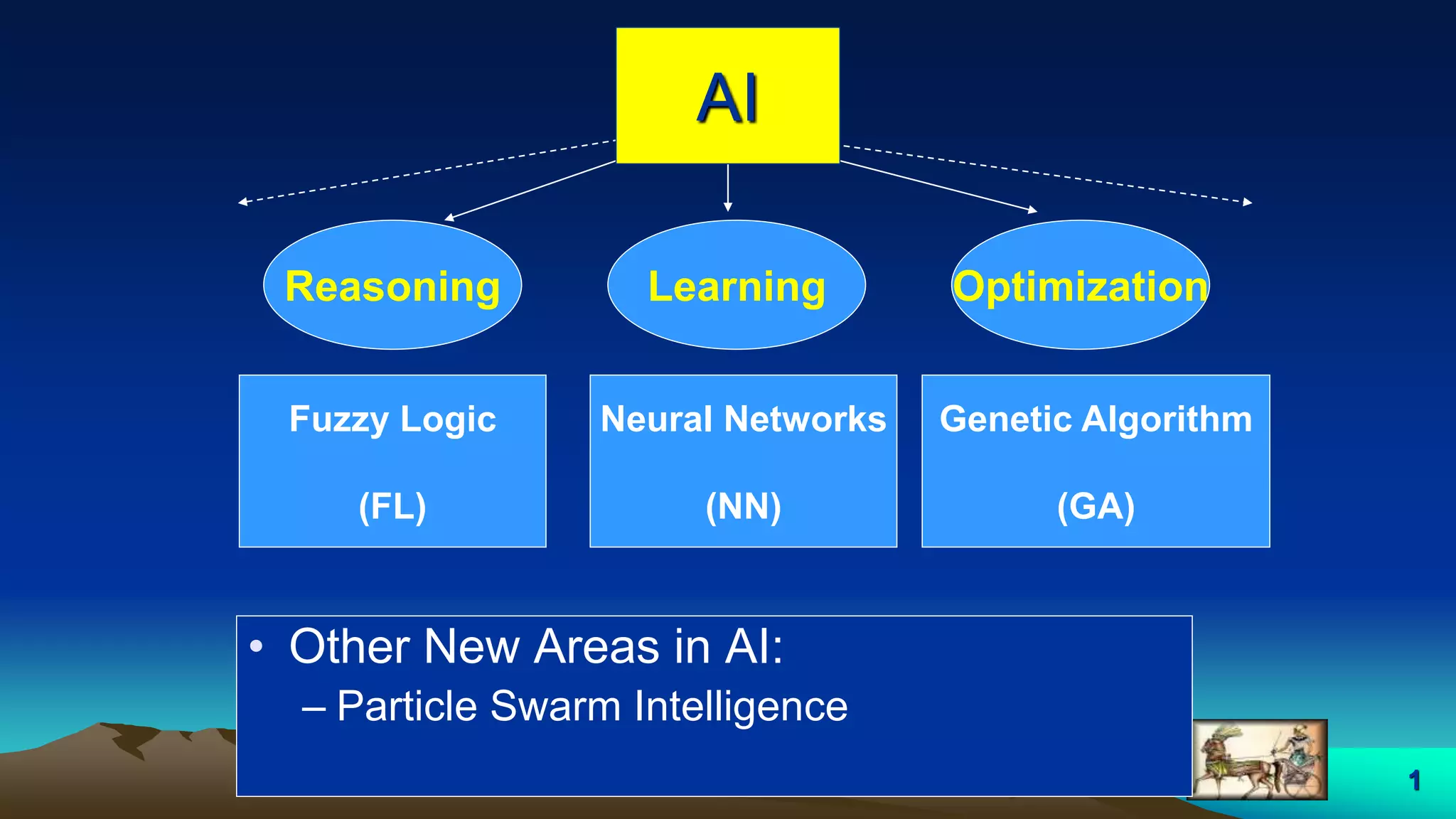
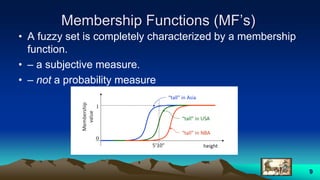
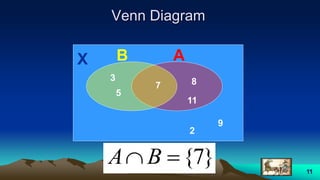
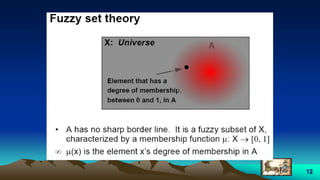
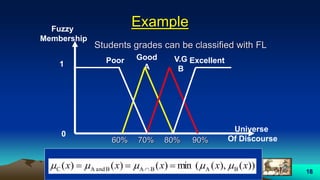
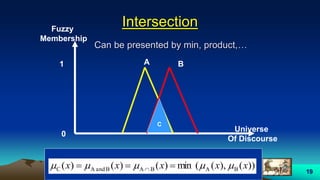
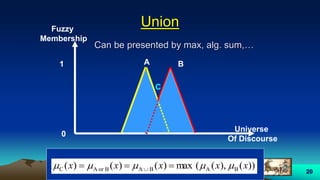
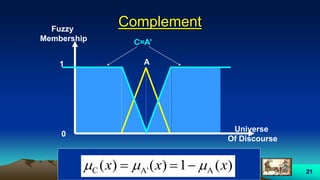
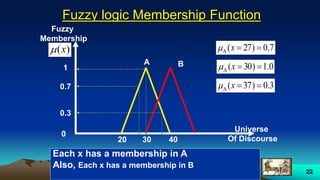
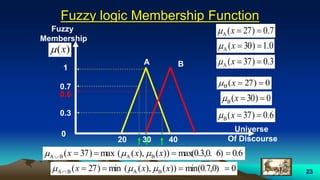
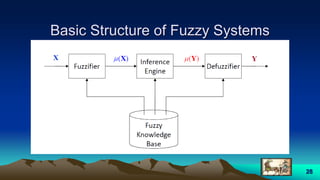
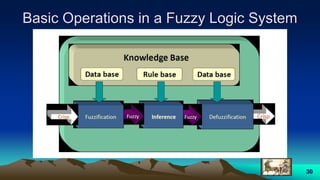
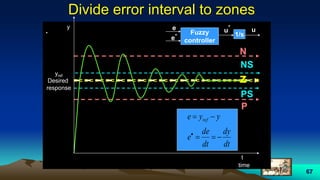
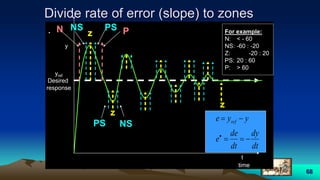
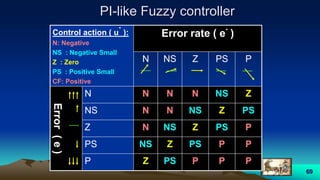
This document provides an overview of fuzzy logic, including its origins, key concepts, and applications. It discusses how fuzzy logic allows for approximate reasoning and decision making under uncertainty by using linguistic variables and fuzzy set theory. Membership functions are used to characterize fuzzy sets and assign degrees of truth between 0 and 1 rather than binary true/false values. Common fuzzy logic operations like intersection, union, and complement are also covered. Finally, some examples of fuzzy logic control systems are presented, including how they are designed using fuzzy rule bases and inference methods like Mamdani and Sugeno.

1. 1
• Other New Areas in AI:
– Particle Swarm Intelligence
Reasoning Learning Optimization
Fuzzy Logic
(FL)
Neural Networks
(NN)
Genetic Algorithm
(GA)
AI

2. 2
Fuzzy Logic
• Fuzzy Logic was initiated in 1965 by Lotfy
Zadeh, professor for computer science at
the University of California in Berkeley.
• Fuzzy stated on the reasoning of facts.
• There is nothing in the world is definite,
there is nothing is absolute. All is a matter
of membership degree to a certain
reference (we must have reference)

3. 3
Fuzzy Logic
• There are two main characteristics of
fuzzy systems that give them better
performance for specific applications:
– Fuzzy systems are suitable for uncertain or
approximate reasoning, especially for the
system with a mathematical model that is
difficult to derive.
– Fuzzy logic allows decision making with
estimated values under incomplete or
uncertain information.

4. 4
Who is Who in Fuzzy Logic
• Lotfy Zadah:
– Established the concept of Fuzzy Logic.
• Mamdani:
– 1st one used fuzzy logic concepts for reasoning
in control (control of steam turbine).
• Sugeno:
– 1st one used fuzzy logic concepts in plane
control.

5. Crisp and fuzzy set
• Crisp Logic
• –A proposition can be true or false only.
• Bob is a student (true)
• Smoking is healthy (false)
• The degree of truth is 0 or 1.
• Fuzzy Logic
• The degree of truth is between 0 and 1.
• • William is young (0.3 truth)
• • Ariel is smart (0.9 truth)
5

6. Crisp set
• Crisp Sets
• Classical sets are called crisp sets
• either an element belongs to a set or not, i.e.,
• Member Function of crisp set
6

7. Crisp set
7

8. Fuzzy set
8

9. Membership Functions (MF’s)
• A fuzzy set is completely characterized by a membership
function.
• – a subjective measure.
• – not a probability measure
9

10. 10

11. 11
Venn Diagram
7
3
5
8
11
2
9
X AB
}7{ BA

12. 12

13. 13
Fuzzy Logic Versus Probability
• Fuzzy  Probability
• Fuzzy is said to measure “possibility” rather than
“probability”.
• Example :
– The probability that a fair die will show six is 1/6. This is a
crisp probability. All credible mathematicians will agree
on this exact number.
• While in Fuzzy Logic nothing is definite at all, it is
designed based on an expert vision which could
differ form another expert.

14. 14
Correspondence between set theory and logic in the fuzzy case
like in the classical case
Where :
Is the Membership Function
Of the classical/fuzzy set A
in the variable x
)(xA

15. comparsion
15

16. 16

17. MF formulation
17

18. 18
Example
Good
A
V.G
B
Universe
Of Discourse
1
0
Fuzzy
Membership
Students grades can be classified with FL
))(,)((min)()()( BABABandAC xxxxx   
60% 70% 80% 90%
ExcellentPoor

19. 19
Intersection
A B
Universe
Of Discourse
1
0
Fuzzy
Membership
Can be presented by min, product,…
C
))(,)((min)()()( BABABandAC xxxxx   

20. 20
Union
A B
Universe
Of Discourse
1
0
Fuzzy
Membership
Can be presented by max, alg. sum,…
))(,)((max)()()( BABABorAC xxxxx   
C

21. 21
Complement
A
Universe
Of Discourse
1
0
Fuzzy
Membership
)(1)()( AA'C xxx  
C=A’

22. 22
Fuzzy logic Membership Function
A
Universe
Of Discourse
1
0
Fuzzy
Membership
Each x has a membership in A
Also, Each x has a membership in B
7.0)27(A x)(x
0.7
0.3
20 30 40
3.0)37(A x
0.1)30(A xB

23. 23
Fuzzy logic Membership Function
0)27(B x
A
Universe
Of Discourse
1
0
Fuzzy
Membership
)(x
0.7
0.3
20 30 40
6.0)37(B x
0)30(B x
B
0.6
7.0)27(A x
3.0)37(A x
0.1)30(A x
0.66)max(0.3,0.))(,)((max)37( BABA  xxx 
0min(0.7,0)))(,)((min)27( BABA  xxx 

24. 24
Fuzzy logic Kinds of operators

25. 25
Fuzzy Logic in control
How to
Design
How to
use
? ?

26. 26
How to design a Fuzzy Logic Controller?
• Basic Steps:
– Determine the linguistic variables & linguistic
values: (from the phenomena under study)
– Construct the rule-base:
(from logic, experience, templates)
– Tune parameters
( By trials or using any other tuning technique
like ANFIS depending on Neural Networks)

27. 27
Fuzzy Linguistic Variables
• Linguistic Variable: The term (noun) used to
represent phenomena under study in a fuzzy sets.
• Linguistic value: is the value (adjective) which can
be assigned to the variable with degree of
membership.
• Examples:
System Linguistic Variable Linguistic Values
Furnace Temperature {cold, worm, hot }
School ExamGrade {fail, poor, good, very
good, excellent}
Car Speed {fast, medium, slow}

28. Basic Structure of Fuzzy Systems
28

29. Basic Structure of Fuzzy Systems
29
• Fuzzifier :Converts the crisp input to a linguistic variable
using the membership functions stored in the fuzzy
knowledge base.
• Defuzzifier : Converts the fuzzy output of the inference
engine to crisp using membership functions analogous to
the ones used by the fuzzifier .
• Fuzzy Knowledge Base that include Information storage for
• 1. Linguistic variables definitions.
• 2. Fuzzy rules.

30. Basic Operations in a Fuzzy Logic System
30

31. Types of inference
• 1.Mamadani Fuzzy Model
• 2.Sugeno Fuzzy Model
• 3.Tsukamoto Fuzzy Model
31

32. Fuzzy inference Mamadani
• One of the most commonly used fuzzy inference
technique is the so-called Mamdani method. In 1975,
Professor Ebrahim Mamdani of London University built
one of the first fuzzy systems to control a steam
engine and boiler combination. He applied a set of
fuzzy rules supplied by experienced human operators.
32

33. Fuzzy inference Mamadani
• The Mamdani-style fuzzy inference process is performed
in four steps:
• fuzzification of the input variables,
• rule evaluation;
• aggregation of the rule outputs, and finally
• defuzzification.
33

34. Mamadani FIS
• Rule base
• If X is A1 and Y is B1 then Z is C1
• If X is A2 and Y is B2 then Z is C2
34

35. Sugeno fuzzy inference
• Mamdani-style inference, as we have just seen, requires
us to find the centroid of a two-dimensional shape by
integrating across a continuously varying function. In
general, this process is not computationally efficient.
• Michio Sugeno suggested to use a single spike, a
singleton, as the membership function of the rule
consequent. A singleton, or more precisely a fuzzy
singleton, is a fuzzy set with a membership function that
is unity at a single particular point on the universe of
discourse and zero everywhere else.
35

36. Sugeno types
• Zero order type
• First order type
36

37. First-Order Sugeno FIS
• Rule base
• If X is A1 and Y is B1 then Z = p1*x + q1*y + r1
• If X is A2 and Y is B2 then Z = p2*x + q2*y + r2
• Fuzzy reasoning
37

38. TSUKAMOTO FIS
• Rule base
• If X is A1 and Y is B1 then Z is C1
• If X is A2 and Y is B2 then Z is C2
38

39. 39
Example 1.1: Restaurant
Fuzzy system in Restaurant
Service and Tips.
Service quality: is a matter of degrees.
Also Tips is a matter of degrees.
But there is some relation between this
input (the service) and that output (the
tips).
Represent the system

40. 40
Ex: Service and Tips in Restaurant
If Antecedent then Consequent
Linguistic Variables
Linguistic Values
If Antecedent then Consequent

41. 41
Ex: Service and Tips in Restaurant
If Antecedent then Consequent
Linguistic Variables
Linguistic Values
If Antecedent then Consequent

42. 42
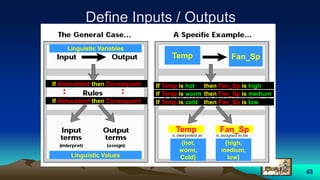
Example 1.2
Air Conditioning
• We have an air conditioned room, we want
to control the temperature of the room in
the range [0:60] degrees.
• Investigate this problem regarding classical
set theory and the fuzzy set theory.

43. 43
Define Inputs / Outputs
Temp Fan_Sp
Temp
{hot,
worm,
Cold}
Fan_Sp
{high,
medium,
low}
If Temp is hot then Fan_Sp is high
If Antecedent then Consequent
Linguistic Variables
Linguistic Values
If Antecedent then Consequent
If Temp is worm then Fan_Sp is medium
If Temp is cold then Fan_Sp is low

44. 44
Ex(1.1): Air Conditioning
Using Classical sets
Cold Worm Hot
Temperature
1
0
Crisp
Membership
20 40 60
This can be a part of an expert system
Linguistic Variable: Temp
Linguistic Value: Cold, Worm, Hot
Think:
What will happen when move among :
0, 10, 15,19.99 , 20, 20.01 ,40 degrees ???! Is this good ?!

45. 45
Using Fuzzy Logic
Cold
Worm
Hot
Temperature
1
0
Fuzzy
Membership
20 40 60
This can be in a Fuzzy system
Linguistic Variable: Temp
Linguistic Value: Cold, Worm, Hot
Think:
This is a fuzzy inference systems replacing the actual
30

46. 46
Output
low
medium
high
FanSpeed
rpm
1
0
Fuzzy
Membership
200 400 600
This can be in a Fuzzy system
Linguistic Variable: FanSpeed
Linguistic Value: low, medium, high
Think:
This is a fuzzy inference systems replacing the actual
300

47. 47
How to use a Fuzzy Logic Controller?
e.g.: by Mamdani criteria (Max of min)
• For each rule: Calculate firing strength of inputs
– And -> min
– Or -> max
• For each rule: Map to degree of match of the Output
– Implication -> min
• Aggregation -> max
• Defuzzification-> centroid
– Now, The Output is mapped.

48. 48
Fuzzy Inference System for
Multi-Input Single Output System
X1 is A1 & …
X1 is A2 & …
X1 is An & …
Y is B1
Y is B2
Y is Bn
Rule #1
Rule #2
Rule #n
Then
Then
Then
Antecedent Consequent
Aggregation
X
Fuzzy
Or
Crisp
Multi
Input
Y
Crisp
Defuzzification
Single
Output
Fuzzy Inference System
(FIS)

49. 49
Assume Multi-Input Single Output
(MISO) with just two rules
A1 A21
Fuzzy
Controller
X
Y
Z
Output
Inputs
X
B1 B21
Y
C1 C21
Z
The Two rules
Rule #1 : If (x is A1) and (y is B1) then z is C1
Rule #2 : If (x is A2) and (y is B2) then z is C2
x y

50. 50
A11
X
B11
Y
C11
Rule #1 : If (x is A1) and (y is B1) then z is C1
x y
A21
X
B21
Y
C21
x y
Rule #2 : If (x is A2) and (y is B2) then z is C2
&
&
Aggregation
Z
Z
With defuzzification
(centroid) We get z z
Z

51. 51
How to use a Fuzzy Logic Controller?
e.g.: by Mamdani criteria (Max of min)
• For each rule: Calculate firing strength of inputs
– And  min
– Or  max
• For each rule: Map to degree of match of the Output
– Implication  min
• Aggregation  max
• Defuzzification  centroid
– Now, The Output is mapped. AGAIN !!!

52. 52
Fuzzy Inference System for
Multi-Input Single Output System
X1 is A1 & …
X1 is A2 & …
X1 is An & …
Y is B1
Y is B2
Y is Bn
Rule #1
Rule #2
Rule #n
Then
Then
Then
Antecedent Consequent
Aggregation
X
Fuzzy
Or
Crisp
Multi
Input
Y
Crisp
Defuzzification
Single
Output
Fuzzy Inference System
(FIS)

53. 53

54. 54
Matlab Demo

55. 55
Example2.1: Multi-Input Multi-Output
MIMO
Washing machine:
Based on clothes Load and Dirtiness the washing program
will set Cycle Time, Soap Amount, and Temperature.
Represent the system using Fuzzy logic

56. 56
Fuzzy
controller
Load Cycle Time
Fuzzy
controller
inputs outputs
Soap amountDirtiness
Temperature
≡
Fuzzy
controller
Load
Soap amountDirtiness
Fuzzy
controller
Load
Dirtiness
Temperature
Fuzzy
controller
Load
Cycle Time
Dirtiness
MIMO
Equivalent
Number of
MISO

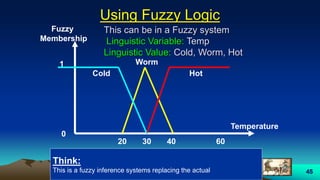
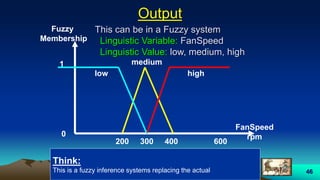
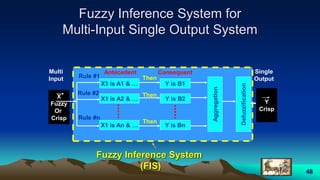
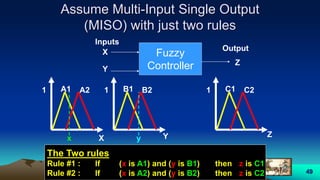
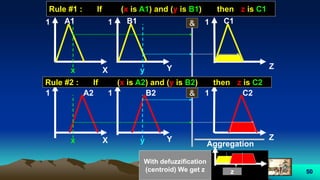
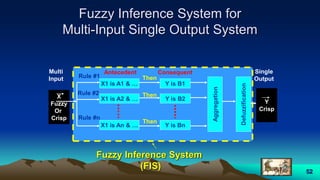
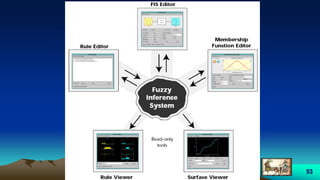
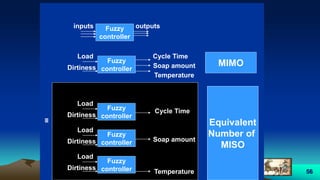
57. 57
• MI (Multi-Input) :
1- Dirtiness:
range: [0 1]
MSF: Triangular (clean, dirty, very dirty)
2- load:
range: [0 1]
MSF: Triangular (light, medium, heavy)
• SO (single Output) :
1- Cycle Time:
range: [0 1]
MSF: Trapezoidal (short, medium , long)

58. 58
• Rules:
Three rules
If (Dirtiness = clean) & (load =light) then CycleTime = short
If (Dirtiness = very dirty) or (load =heavy) then CycleTime = long
If (Dirtiness = dirty) then CycleTime = medium

59. 59
Useful commands
readfis
evalfis

60. 60
Matlab Demo
• g=readfis(‘wmachine.fis’);
• g=
• g.andMethod
• g.input
• g.input(1).name
• g.input(2).range
• g.input(1).mf
• g.rule
• Y=evalfis([0.3;0.9],g)

61. Air condition application
• Component
• Arduino uno
• 2 potentiometer
• Led as output
• Fuzzy logic programming (fis) using Matlab
• Arduino code using specific website
61

62. 62
Scaling Factors
• The scaling factors are the main parameters used to tune
fuzzy logic controller (FLC).
• Changing the scaling factors changes the normalized
universe of discourse.
• For example:
– High value of Ke (input gain) result in low steady state error and rise time
but large overshoot.
– Low value of Kdu (output gain) increase the rise time and integral square
error.
• Tune will be around 80%-120% of the initial values where:
– Ke : input error gain
– Kde : input rate of error gain
– Kdu : output rate of control signal gain
– .
u
.e
Fuzzy
controllere
.
ke
kde
Plantkdu 1/s
u
PI-Like
Fuzzy Controller

63. 63
How to design a Fuzzy Logic Controller?
• Basic Steps:
– Determine the linguistic variables & linguistic
values: (from the phenomena under study)
– Construct the rule-base:
(from logic, experience, templates)
– Tune parameters
( By trials or using any other tuning technique
like ANFIS depending on Neural Networks)

64. 64
Tuning:
==========
1- start with the minimum number of MSFs you expect
2- Adapt ranges to map the phenomena correctly
3- write the minimum number of rule you expect
4- if not enough, write all the rules expected
5- if still not enough change the MSFs types
6- if still not enough increase number of MSFs
7- Write the rules again (consider weights)
8- change the scaling factors
9- change the methods of implication, aggregation, and
defuzzification.
Questions?
=========
is there steady state error? ess
is there overshoot? O.S
is there long delay? (is the rise time accepted or not) tr

65. 65
Settling time: ts
2% criteria
5% criteria
Transient Response
Steady state error: ess
Delay time: td
Rise time: tr
Peak time: tp
Maximum overshoot: Mp
Settling time: ts
Time constant: T
n
s Tt

4
4 
n
s Tt

3
3  td ts
Mp
0.5
tptr
Maximum overshoot:
2% criteria or
5% criteria














2
1
eM p
Time constant:
n
T

1

2nd order system

66. 66
PI- like Fuzzy Control
.
time
yref
Desired
response
dt
dy
dt
de
e
yye ref



y
t
e
Fuzzy
controllere
. u
.
1/s
u

67. 67
Divide error interval to zones
.
time
yref
Desired
response
N
z
PS
P
NS
y
t
dt
dy
dt
de
e
yye ref



u
.e
Fuzzy
controllere
. 1/s
u

68. 68
Divide rate of error (slope) to zones
.
time
yref
Desired
response
N z
z
NS PPS
y
t
PS NS
z
dt
dy
dt
de
e
yye ref



For example:
N: < - 60
NS: -60 : -20
Z: -20 : 20
PS: 20 : 60
P: > 60

69. 69
PI-like Fuzzy controller
Control action ( u
.
):
N: Negative
NS : Negative Small
Z : Zero
PS : Positive Small
CF: Positive
Error rate ( e
.
)
N NS Z PS P
Error(e)
N N N N NS Z
NS N N NS Z PS
Z N NS Z PS P
PS NS Z PS P P
P Z PS P P P

70. 70
TSK model
Takagi, Sugeno, Kang
. Antecedent Consequent
V_low
low
V_high
x
1
Fuzzy
Membership
-1 10
y
1
Fuzzy
Membership
y1 y3y2
α2
=0.8
α1
=0.4
α3
=0.2
...
...
321
332211




 yyy
y
The Three rules
If (x is low) then (y1 = 2*x+5)
If (x is high) then (y2 = 1*x+3)
If (x is v_high) then (y3 = 8)
Note: as x changes
this will affect y’s and also α’s
high

71. 71
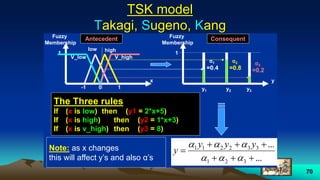
Example:
function approximation
• We want to approximate this
function in the range [1 3] using
fuzzy TSK model with five MSFs.
y = x2
y
x

72. 72
Example:
function approximation
• We need five equations one for each
subrange.
Solution:
y = x2
y
x
)(|
:
ixi xx
dx
dy
yy
x
dx
dy
y
x
y
dx
dy
Taylor
i





x y=x2
1 1 2
1.5 2.25 3
2 4 4
2.5 6.25 5
3 9 6
x
dx
dy
2 )(| ixi xx
dx
dy
yy i

12
)1(21


xy
xy
25.23
)5.1(325.2


xy
xy
44
)2(44


xy
xy
25.65
)5.2(525.6


xy
xy
96
)3(69


xy
xy

73. 73
.
Antecedent: x Consequent: y
x
1
Fuzzy
Membership
1 2.50
y
1
Fuzzy
Membership
y1 y5y2
The five rules
If (x is one) then (y1 = 2*x - 1)
If (x is 1hf) then (y2 = 3*x - 2.25)
If (x is two) then (y3 = 4*x - 4)
If (x is 2hf) then (y4 = 5*x - 6.25)
If (x is three) then (y5 = 6*x - 9)
one
1.5 2 3
1hf two 2hf three
y3 y4

74. 74
Matlab Demo

75. 75
References
1. J.-S. Roger Jang, Ned Gulley “Artificial Intelligence -
Fuzzy Logic Toolbox, Matlab”, Mathwotks,1997.
2. R. Full´er “Neural Fuzzy Systems” Abo, 1995.
3. ITI ,“Nine Month Program Training Kit”, 2007.
4. H.Larsen “Fundamentals of fuzzy sets and fuzzy logic”
Aalborg University, 2005.
5. Prof. A. Hambaba” Networked–Intelligent Software
Agents & Agents” San Jose state, 2002.
6. Prof. P. Smyth, “Introduction to Artificial Intelligence”,
UCIrvine, 2007.
7. R. J. Marks “Introduction to Fuzzy Inference”, Baylor
University
8. http://en.wikipedia.org/