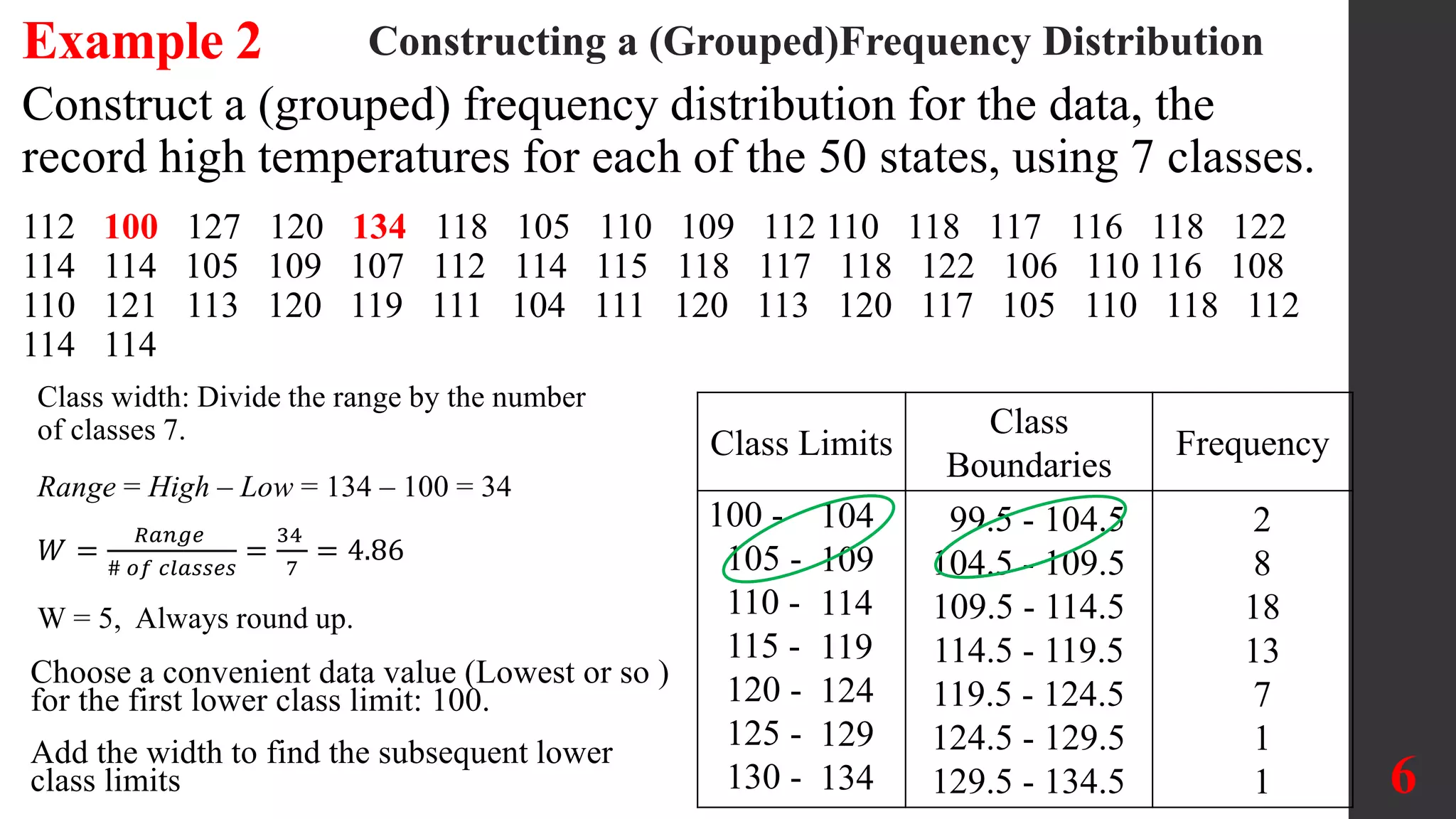
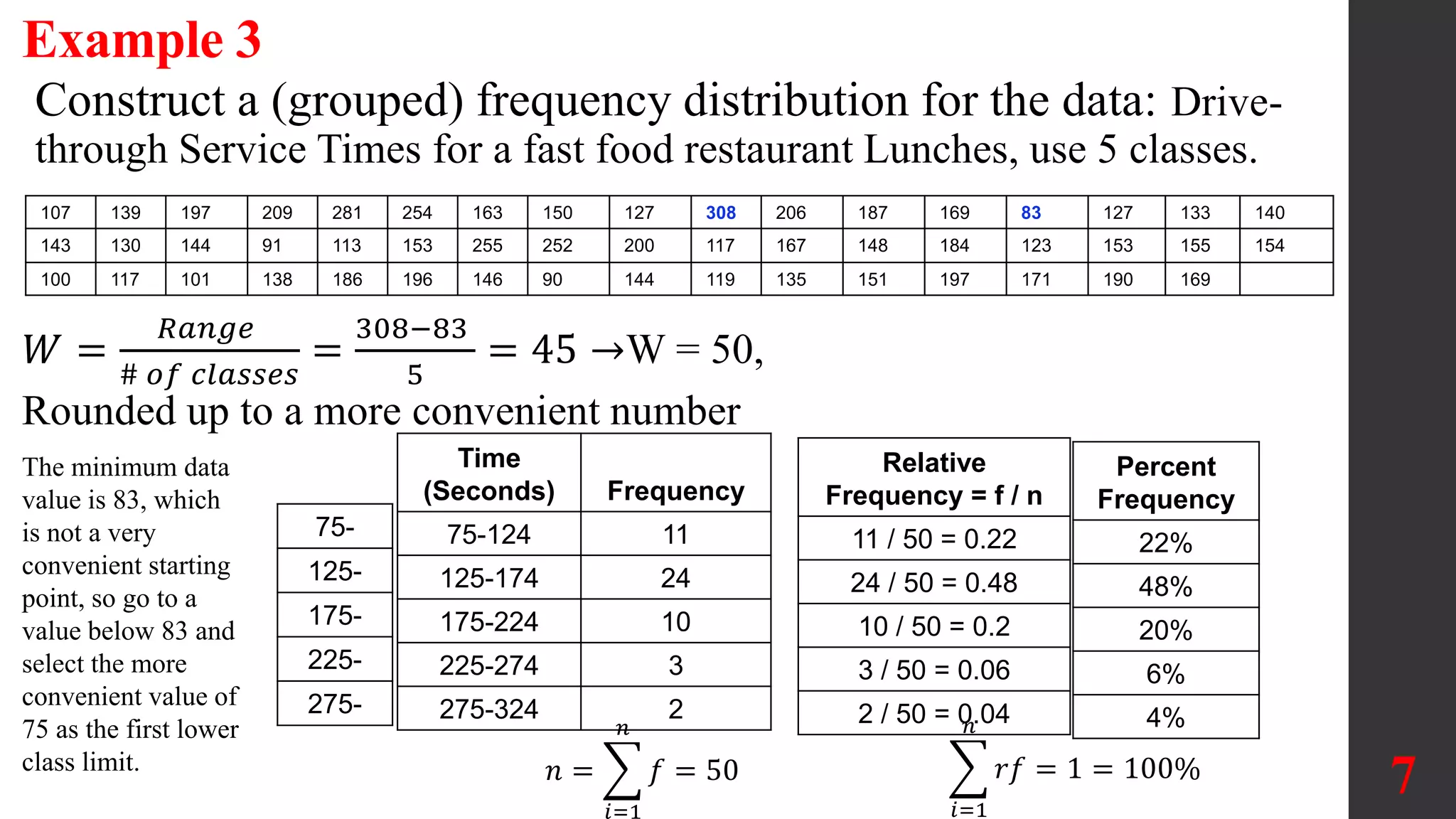
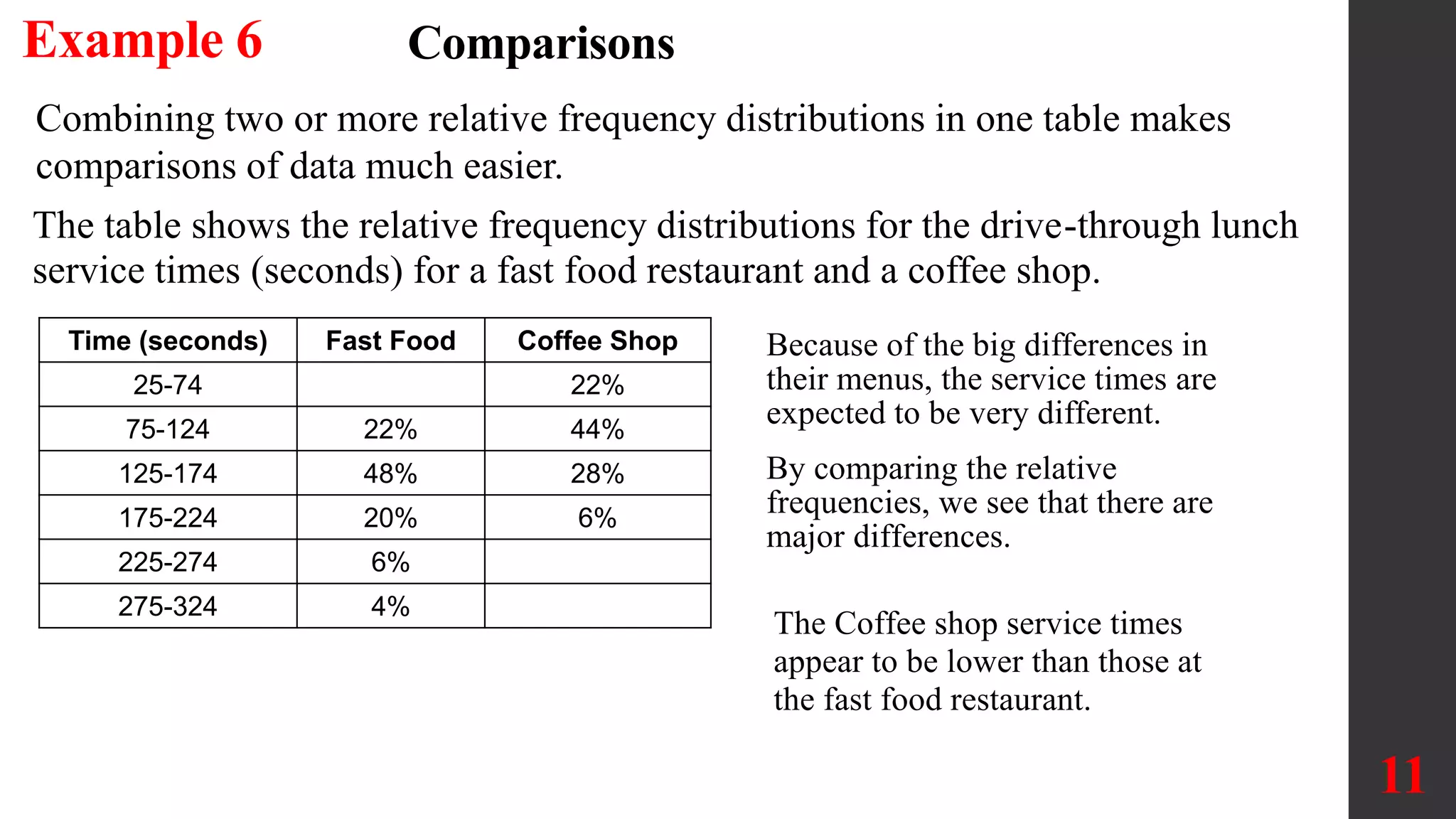
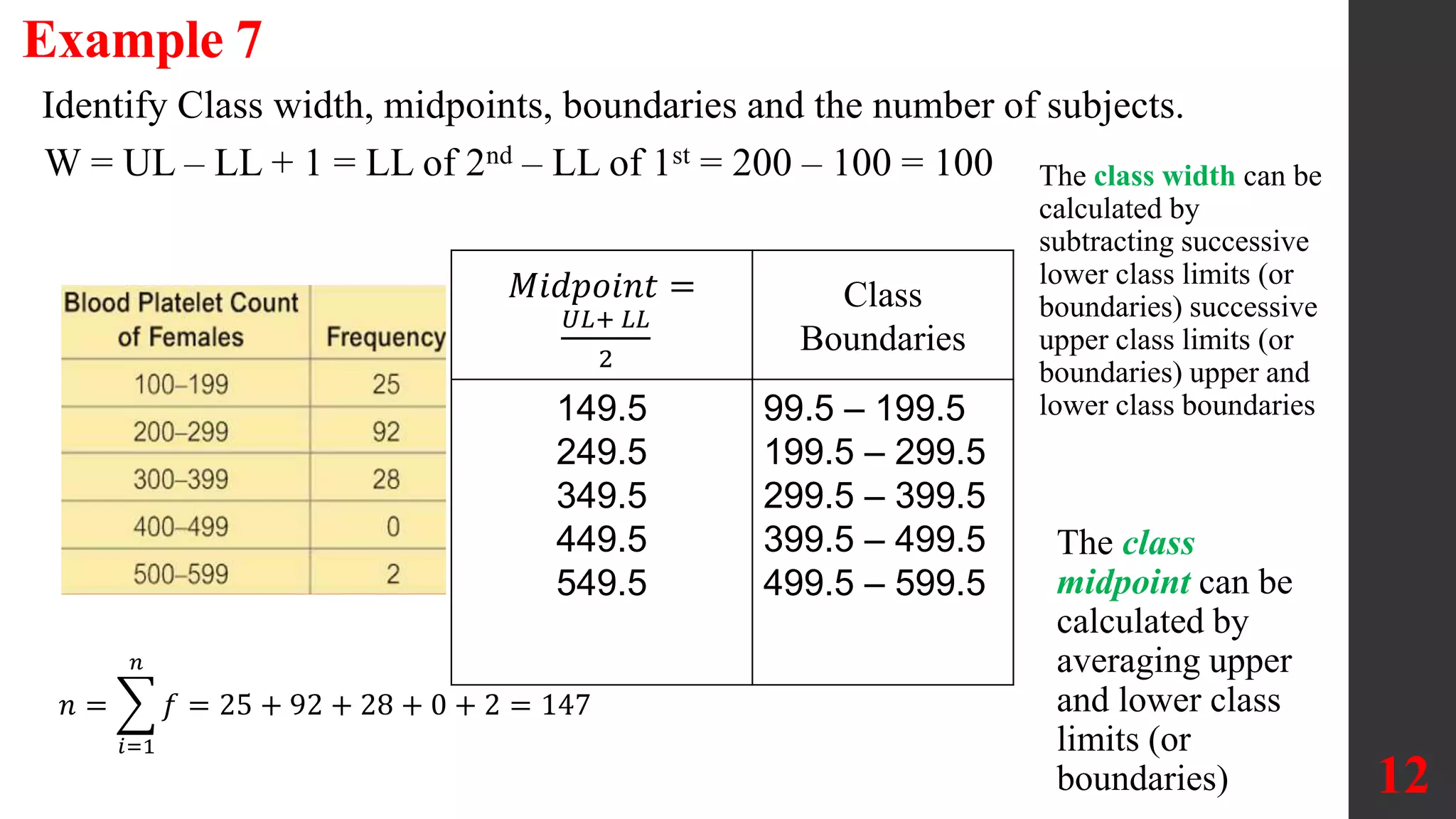
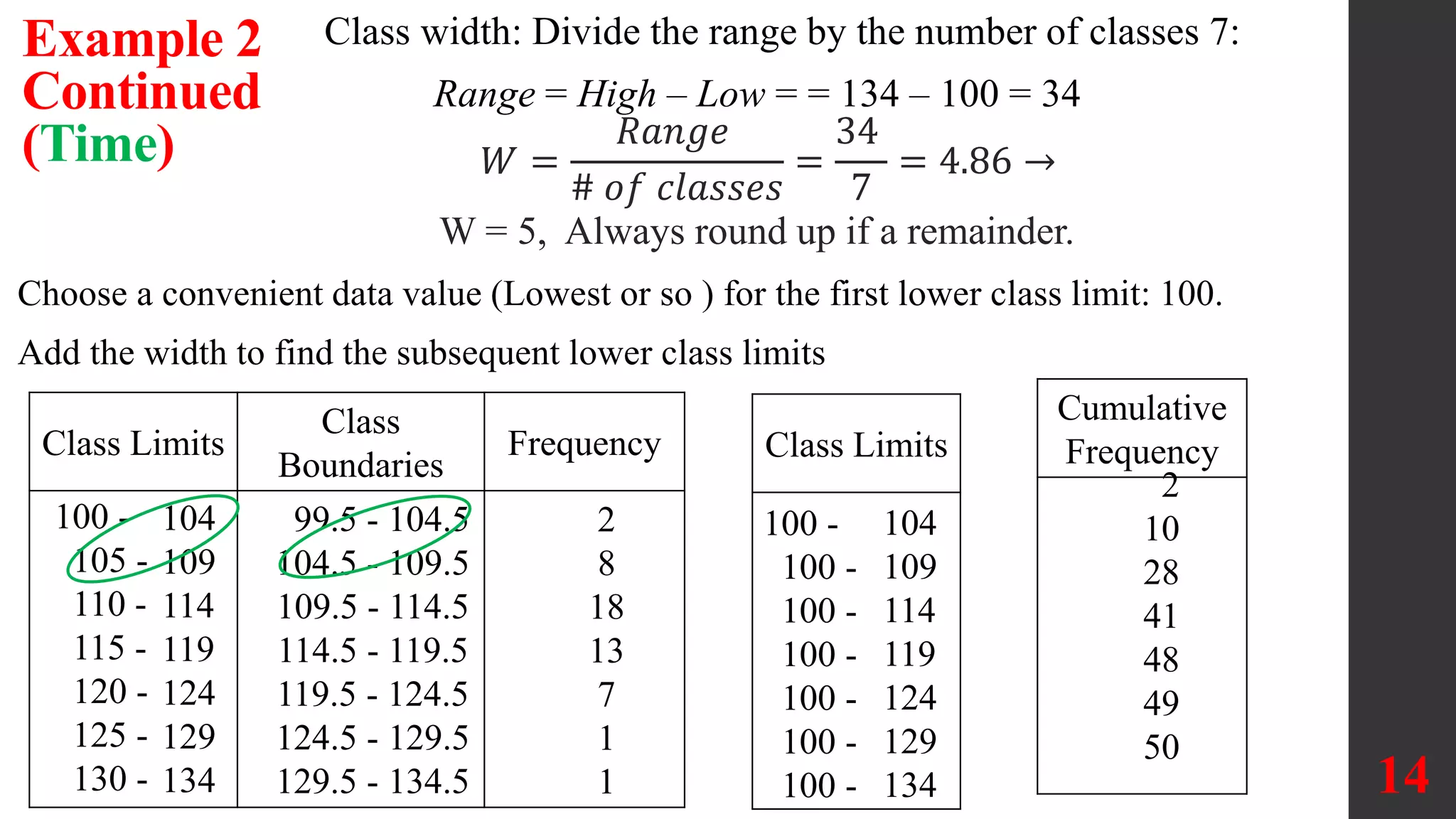
The document discusses organizing and summarizing data using frequency distributions. It defines key terms like frequency distribution, class width, boundaries, and midpoints. Examples are provided to demonstrate how to construct frequency distributions, calculate values, and interpret results. Comparing distributions can reveal differences in datasets. Gaps may indicate separate populations in the data. [END SUMMARY]

1. Elementary Statistics
Chapter 2: Exploring
Data with Tables and
Graphs
2.1 Frequency
Distributions for
Organizing and
Summarizing Data
1

2. Chapter 2:
Exploring Data with Tables and Graphs
2.1 Frequency Distributions for Organizing and
Summarizing Data
2.2 Histograms
2.3 Graphs that Enlighten and Graphs that Deceive
2.4 Scatterplots, Correlation, and Regression
2
Objectives:
1. Organize data using a frequency distribution.
2. Represent data in frequency distributions graphically using histograms, frequency polygons, and ogives.
3. Represent data using bar graphs, Pareto charts, time series graphs, and pie graphs.
4. Draw and interpret a stem and leaf plot.
5. Draw and interpret a scatter plot for a set of paired data.

3. 3
2.1 Frequency Distributions for Organizing and Summarizing Data
Data collected in original form is called raw data.
Frequency Distribution (or Frequency Table)
A frequency distribution is the organization of raw data in table form,
using classes and frequencies. It Shows how data are partitioned among
several categories (or classes) by listing the categories along with the
number (frequency) of data values in each of them.
Nominal- or ordinal-level data that can be placed in categories is
organized in categorical frequency distributions.
Key Concept: When working with large data sets, a frequency distribution
(or frequency table) is often helpful in organizing and summarizing data. A
frequency distribution helps us to understand the nature of the distribution of
a data set.

4. 4
Categorical Frequency Distribution:
Example 1
Construct a frequency distribution for the data produced by 25 people’s
blood test that results in their blood type as follows:
Raw Data: A,B,B,AB,O O,O,B,AB,B B,B,O,A,O A,O,O,O,AB AB,A,O,B,A
Class Tally Frequency Percent Frequency = f / n
A
B
O
AB
IIIII
IIIII II
IIIII IIII
IIII
5
7
9
4
20%
28%
36%
16%
𝑛 =
𝑖=1
𝑛
𝑓 = 25
𝑖=1
𝑛
𝑟𝑓 = 1 = 100%

5. 2.1 Frequency Distributions for Organizing and Summarizing Data
Definitions: Lower class limits: The smallest numbers that can belong to each of the different classes
Upper class limits: The largest numbers that can belong to each of the different classes
Class boundaries: The numbers used to separate the classes, but without the gaps created by class limits
Class midpoints: The values in the middle of the classes Each class midpoint can be found by adding the lower class
limit to the upper class limit and dividing the sum by 2.
Class width: The difference between two consecutive lower class limits in a frequency distribution
1. Select the number of classes, usually between 5 and 20.
2. Calculate the class width: 𝑊 =
𝑀𝑎𝑥−𝑀𝑖𝑛
# 𝑜𝑓 𝑐𝑙𝑎𝑠𝑠𝑒𝑠
and round up accordingly.
3. Choose the value for the first lower class limit by using either the minimum value or a convenient value below
the minimum.
4. Using the first lower class limit and class width, list the other lower class limits.
5. List the lower class limits in a vertical column and then determine and enter the upper class limits.
6. Take each individual data value and put a tally mark in the appropriate class. Add the tally marks to get the
frequency.
Procedure for Constructing a Frequency Distribution
5

6. Class width: Divide the range by the number
of classes 7.
Range = High – Low = 134 – 100 = 34
𝑊 =
𝑅𝑎𝑛𝑔𝑒
# 𝑜𝑓 𝑐𝑙𝑎𝑠𝑠𝑒𝑠
=
34
7
= 4.86
W = 5, Always round up.
Choose a convenient data value (Lowest or so )
for the first lower class limit: 100.
Add the width to find the subsequent lower
class limits
Class Limits
Class
Boundaries
Frequency
100 -
105 -
110 -
115 -
120 -
125 -
130 -
104
109
114
119
124
129
134
99.5 - 104.5
104.5 - 109.5
109.5 - 114.5
114.5 - 119.5
119.5 - 124.5
124.5 - 129.5
129.5 - 134.5
2
8
18
13
7
1
1 6
Constructing a (Grouped)Frequency Distribution
Example 2
Construct a (grouped) frequency distribution for the data, the
record high temperatures for each of the 50 states, using 7 classes.
112 100 127 120 134 118 105 110 109 112 110 118 117 116 118 122
114 114 105 109 107 112 114 115 118 117 118 122 106 110 116 108
110 121 113 120 119 111 104 111 120 113 120 117 105 110 118 112
114 114

7. Example 3
7
Construct a (grouped) frequency distribution for the data: Drive-
through Service Times for a fast food restaurant Lunches, use 5 classes.
107 139 197 209 281 254 163 150 127 308 206 187 169 83 127 133 140
143 130 144 91 113 153 255 252 200 117 167 148 184 123 153 155 154
100 117 101 138 186 196 146 90 144 119 135 151 197 171 190 169 Blank
𝑊 =
𝑅𝑎𝑛𝑔𝑒
# 𝑜𝑓 𝑐𝑙𝑎𝑠𝑠𝑒𝑠
=
308−83
5
= 45 →W = 50,
Rounded up to a more convenient number
The minimum data
value is 83, which
is not a very
convenient starting
point, so go to a
value below 83 and
select the more
convenient value of
75 as the first lower
class limit.
75-
125-
175-
225-
275-
Time
(Seconds) Frequency
75-124 11
125-174 24
175-224 10
225-274 3
275-324 2
Relative
Frequency = f / n
11 / 50 = 0.22
24 / 50 = 0.48
10 / 50 = 0.2
3 / 50 = 0.06
2 / 50 = 0.04
Percent
Frequency
22%
48%
20%
6%
4%
𝑛 =
𝑖=1
𝑛
𝑓 = 50
𝑖=1
𝑛
𝑟𝑓 = 1 = 100%

8. Find the Cumulative Frequency Distribution for example 3.
Time (Seconds)
Cumulative
Frequency
Less than 125
Less than 175
Less than 225
Less than 275
Less than 325
8
Example 4
11
35
45
48
50
11
35
45
48
50
Time
(Seconds) Frequency
75-124 11
125-174 24
175-224 10
225-274 3
275-324 2
Time
(Seconds)
Cumulative
Frequency
75-124
75-174
75-224
75-274
75-324
Time (Seconds)
Cumulative
Frequency
Less than 124.5
Less than 174.5
Less than 224.5
Less than 274.5
Less than 324.5
11
35
45
48
50
3 ways of writing CFDT

9. Critical Thinking: Using Frequency Distributions to Understand Data
In statistics we are often interested in determining whether the data have a
Normal Distribution.
1. The frequencies start low, then increase to one or two high frequencies, and then
decrease to a low frequency.
2. The distribution is approximately symmetric. Frequencies preceding the maximum
frequency should be roughly a mirror image of those that follow the maximum
frequency.
9
2.1 Frequency Distributions for Organizing and Summarizing Data
Gaps:
1. The presence of gaps can show that the data are from two or more different
populations.
2. However, the converse is not true, because data from different populations
do not necessarily result in gaps.

10. Exploring Data: What Does a Gap Tell Us?
The table shown is a frequency distribution of the weights (grams) of randomly
selected pennies.
Weight (grams) of
Penny
Frequency
2.40-2.49 18
2.50-2.59 19
2.60-2.69 0
2.70-2.79 0
2.80-2.89 0
2.90-2.99 2
3.00-3.09 25
3.10-3.19 8
10
Example 5
Examination of the frequencies reveals a
large gap between the lightest pennies and the
heaviest pennies.
This suggests that we have two different
populations:
Facts:
Pennies made before 1983 are 95% copper and 5% zinc.
Pennies made after 1983 are 2.5% copper and 97.5% zinc.

11. Comparisons
Combining two or more relative frequency distributions in one table makes
comparisons of data much easier.
11
Example 6
The table shows the relative frequency distributions for the drive-through lunch
service times (seconds) for a fast food restaurant and a coffee shop.
Time (seconds) Fast Food Coffee Shop
25-74 Blank 22%
75-124 22% 44%
125-174 48% 28%
175-224 20% 6%
225-274 6% Blank
275-324 4% Blank
Because of the big differences in
their menus, the service times are
expected to be very different.
By comparing the relative
frequencies, we see that there are
major differences.
The Coffee shop service times
appear to be lower than those at
the fast food restaurant.

12. Identify Class width, midpoints, boundaries and the number of subjects.
12
Example 7
𝑀𝑖𝑑𝑝𝑜𝑖𝑛𝑡 =
𝑈𝐿+ 𝐿𝐿
2
Class
Boundaries
149.5
249.5
349.5
449.5
549.5
99.5 – 199.5
199.5 – 299.5
299.5 – 399.5
399.5 – 499.5
499.5 – 599.5
W = UL – LL + 1 = LL of 2nd – LL of 1st = 200 – 100 = 100
𝑛 =
𝑖=1
𝑛
𝑓 = 25 + 92 + 28 + 0 + 2 = 147
The class width can be
calculated by
subtracting successive
lower class limits (or
boundaries) successive
upper class limits (or
boundaries) upper and
lower class boundaries
The class
midpoint can be
calculated by
averaging upper
and lower class
limits (or
boundaries)

13. 13
Example 8
There are disproportionately more 0’s and 5’s, the weights were
reported instead of measured.
Therefore, the results are not accurate.

14. Class width: Divide the range by the number of classes 7:
Range = High – Low = = 134 – 100 = 34
𝑊 =
𝑅𝑎𝑛𝑔𝑒
# 𝑜𝑓 𝑐𝑙𝑎𝑠𝑠𝑒𝑠
=
34
7
= 4.86 →
W = 5, Always round up if a remainder.
Choose a convenient data value (Lowest or so ) for the first lower class limit: 100.
Add the width to find the subsequent lower class limits
Example 2
Continued
(Time)
Class Limits
Class
Boundaries
Frequency
100 -
105 -
110 -
115 -
120 -
125 -
130 -
104
109
114
119
124
129
134
99.5 - 104.5
104.5 - 109.5
109.5 - 114.5
114.5 - 119.5
119.5 - 124.5
124.5 - 129.5
129.5 - 134.5
2
8
18
13
7
1
1
2
10
28
41
48
49
50
14
Cumulative
Frequency
Class Limits
100 -
100 -
100 -
100 -
100 -
100 -
100 -
104
109
114
119
124
129
134