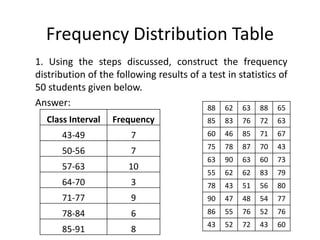
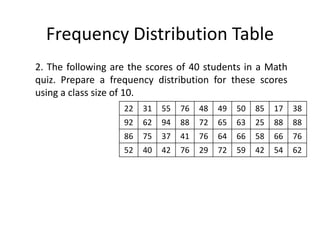
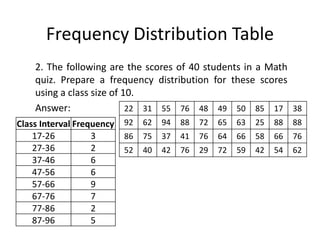
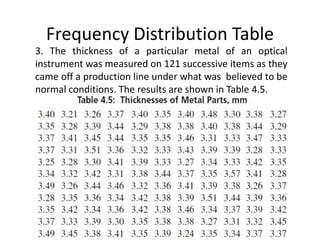
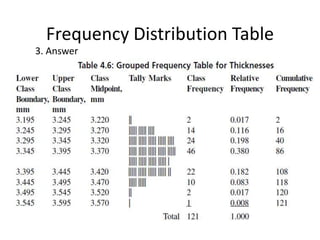
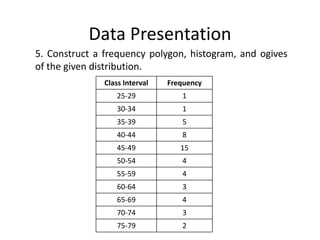
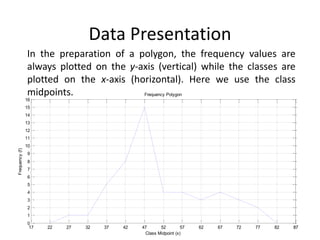
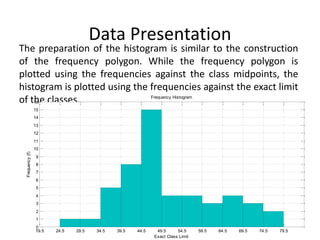
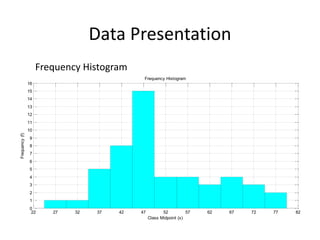
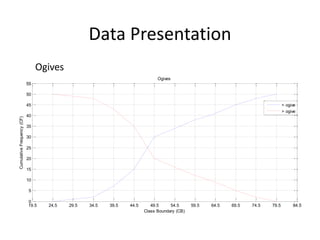
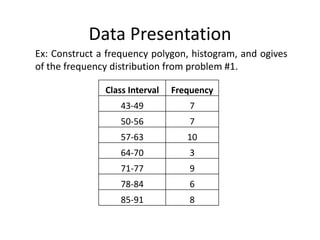
The document discusses frequency distribution tables, including how to construct them from raw data by grouping data into classes of equal intervals and determining the frequency of observations within each class. Key aspects covered include determining class limits, boundaries, frequencies, widths, and cumulative frequencies. Examples are provided to demonstrate how to build a frequency distribution table and corresponding graphical representations like histograms, frequency polygons, and ogives from sets of data.

1. STAT 1 – Elementary Statistics
Frequency Distribution

2. Recall: Types of Data Presentation
• Textual Form
- Data presentation using sentences and paragraphs in
describing data
• Tabular Form
- Data presentation that uses tables arranged in rows
and columns for various parameters
• Graphical Form
- Pictorial representation of data

3. Grouped and Ungrouped Data
• Ungrouped Data
- Data points are treated individually.
• Grouped Data
- Data points are treated and grouped according to
categories.

4. Frequency Distribution Table
Frequency Distribution Table
Numerous data can be analyzed by grouping the data
into different classes with equal class intervals and
determining the number of observations that fall within
each class. This procedure is done to lessen work done
in treating each data individually by treating the data by
group.

5. Frequency Distribution Table
Class limits
- The smallest and the largest values that fall within
the class interval (class)
- Taken with equal number of significant figures as the
given data.
Class boundaries (true class limits)
- More precise expression of the class interval
- It is usually one significant digit more than the class
limit.
- Acquired as the midpoint of the upper limit of the
lower class and the lower limit of the upper class

6. Frequency Distribution Table
Frequency
- The number of observations falling within a particular
class.
- Counting and tallying
Class width (class size)
- Numerical difference between the upper and lower class
boundaries of a class interval.
Class mark (class midpoint)
- Middle element of the class
- It represents the entire class and it is usually
symbolized by x.

7. Frequency Distribution Table
Cumulative Frequency Distribution
- can be derived from the frequency distribution and can
be also obtained by simply adding the class frequencies
- Partial sums
Types of Cumulative Frequency Distribution
- Less than cumulative frequency (<cf) refers to the
distribution whose frequencies are less than or below
the upper class boundary they correspond to.
- Greater than cumulative frequency (>cf) refers to the
distribution whose frequencies are greater than or
above the lower class boundary the correspond to.

8. Frequency Distribution Table
Relative Frequency
- Percentage frequency of the class with respect to the
total population
- For presenting pie charts
Relative Frequency (%rf) Distribution
- The proportion in percent the frequency of each class
to the total frequency
- Obtained by dividing the class frequency by the total
frequency, and multiplying the answer by 100

9. Frequency Distribution Table
Class Interval Frequency x LCB UCB <cf >cf %rf

10. FDT
Class
Limits
Class
Boundaries
Tally
Marks
f X <c.f. >c.f. rf %rf

11. Frequency Distribution Table
Steps in Constructing a Frequency Distribution Table (FDT)
1. Get the lowest and the highest value in the
distribution. We shall mark the highest and lowest
value in the distribution.
2. Get the value of the range. The range denoted by R,
refers to the difference between the highest and the
lowest value in the distribution. Thus,
R = H ─ L.

12. Frequency Distribution Table
3. Determine the number of classes. In the
determination of the number of classes, it should be
noted that there is no standard method to follow.
Generally, the number of classes must not be less than
5 and should not be more than 15. In some instances,
however, the number of classes can be approximated
by using the relation
𝑘 = 1 + 3.322 log 𝑛 (Sturges’ Formula),
where k = number of classes and n = sample size. is
the ceiling operator (meaning take the closest integer
above the calculated value).
Square root principle: 𝑘 = 𝑛

13. Frequency Distribution Table
4. Determine the size of the class interval. The value of C
can be obtained by dividing the range by the desired
number of classes. Hence, 𝐶 = 𝑅 𝑘.
5. Construct the classes. In constructing the classes, we
first determine the lower limit of the distribution. The
value of this lower limit can be chosen arbitrarily as
long as the lowest value shall be on the first interval
and the highest value to the last interval.

14. Frequency Distribution Table
6. Determine the frequency of each class. The
determination of the number of frequencies is done
by counting the number of items that shall fall in each
interval.

15. Frequency Distribution Table
Ex: 1. Using the steps discussed, construct the frequency
distribution of the following results of a test in statistics of
50 students given below.
88 62 63 88 65
85 83 76 72 63
60 46 85 71 67
75 78 87 70 43
63 90 63 60 73
55 62 62 83 79
78 43 51 56 80
90 47 48 54 77
86 55 76 52 76
43 52 72 43 60

16. Frequency Distribution Table
1. Using the steps discussed, construct the frequency
distribution of the following results of a test in statistics of
50 students given below.
Answer: 88 62 63 88 65
85 83 76 72 63
60 46 85 71 67
75 78 87 70 43
63 90 63 60 73
55 62 62 83 79
78 43 51 56 80
90 47 48 54 77
86 55 76 52 76
43 52 72 43 60
Class Interval Frequency
43-49 7
50-56 7
57-63 10
64-70 3
71-77 9
78-84 6
85-91 8

17. Frequency Distribution Table
2. The following are the scores of 40 students in a Math
quiz. Prepare a frequency distribution for these scores
using a class size of 10.
22 31 55 76 48 49 50 85 17 38
92 62 94 88 72 65 63 25 88 88
86 75 37 41 76 64 66 58 66 76
52 40 42 76 29 72 59 42 54 62

18. Frequency Distribution Table
2. The following are the scores of 40 students in a Math
quiz. Prepare a frequency distribution for these scores
using a class size of 10.
Answer: 22 31 55 76 48 49 50 85 17 38
92 62 94 88 72 65 63 25 88 88
86 75 37 41 76 64 66 58 66 76
52 40 42 76 29 72 59 42 54 62
Class Interval Frequency
17-26 3
27-36 2
37-46 6
47-56 6
57-66 9
67-76 7
77-86 2
87-96 5

19. Frequency Distribution Table
3. The thickness of a particular metal of an optical
instrument was measured on 121 successive items as they
came off a production line under what was believed to be
normal conditions. The results are shown in Table 4.5.

20. Frequency Distribution Table
3. Answer

21. Data Presentation
Graphical Form of Frequency Distribution
Frequency Polygon
- Line graph
- The points are plotted at the midpoint of the classes.
Histogram (Frequency Histogram or Relative Frequency
Histogram)
- Bar graph
- Plotted at the exact lower limits of the classes

22. Data Presentation
Graphical Form of Frequency Distribution
Ogive
- Line graph
- Graphical representation of the cumulative frequency
distribution
- The < ogive represents the <cf while the > ogive
represents the >cf.

23. Data Presentation
5. Construct a frequency polygon, histogram, and ogives
of the given distribution.
Class Interval Frequency
25-29 1
30-34 1
35-39 5
40-44 8
45-49 15
50-54 4
55-59 4
60-64 3
65-69 4
70-74 3
75-79 2

24. Data Presentation
In the preparation of a polygon, the frequency values are
always plotted on the y-axis (vertical) while the classes are
plotted on the x-axis (horizontal). Here we use the class
midpoints.
17 22 27 32 37 42 47 52 57 62 67 72 77 82 87
87
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Class Midpoint (x)
Frequency
(f)
Frequency Polygon

25. Data Presentation
The preparation of the histogram is similar to the construction
of the frequency polygon. While the frequency polygon is
plotted using the frequencies against the class midpoints, the
histogram is plotted using the frequencies against the exact limit
of the classes.
19.5 24.5 29.5 34.5 39.5 44.5 49.5 54.5 59.5 64.5 69.5 74.5 79.5
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Exact Class Limit
Frequency
(f)
Frequency Histogram

26. Data Presentation
Frequency Histogram
22 27 32 37 42 47 52 57 62 67 72 77 82
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Class Midpoint (x)
Frequency
(f)
Frequency Histogram

27. Data Presentation
Ogives
19.5 24.5 29.5 34.5 39.5 44.5 49.5 54.5 59.5 64.5 69.5 74.5 79.5 84.5
0
5
10
15
20
25
30
35
40
45
50
55
55
Class Boundary (CB)
Cumulative
Frequency
(CF)
Ogives
< ogive
> ogive

28. Data Presentation
Ex: Construct a frequency polygon, histogram, and ogives
of the frequency distribution from problem #1.
Class Interval Frequency
43-49 7
50-56 7
57-63 10
64-70 3
71-77 9
78-84 6
85-91 8