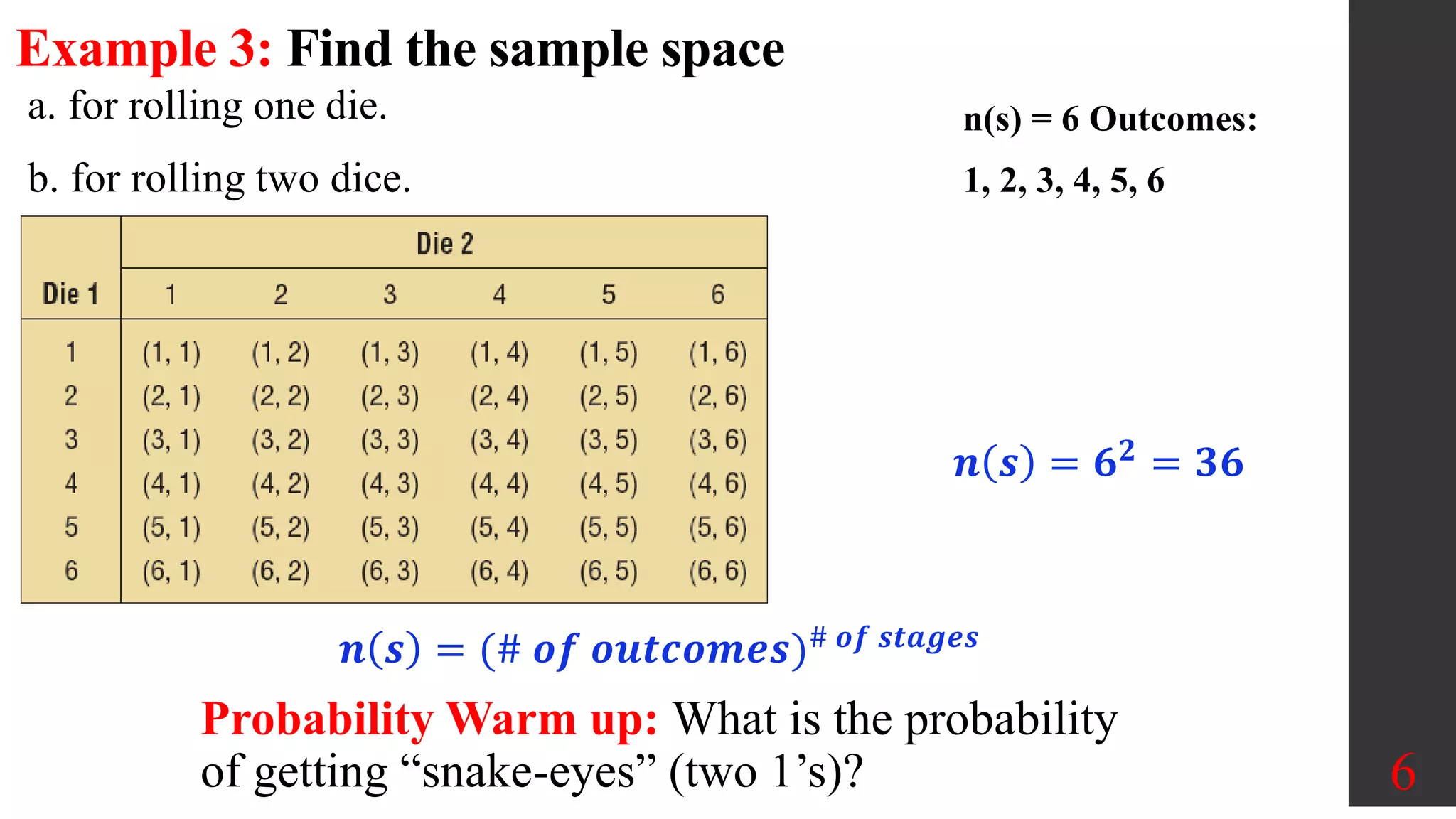
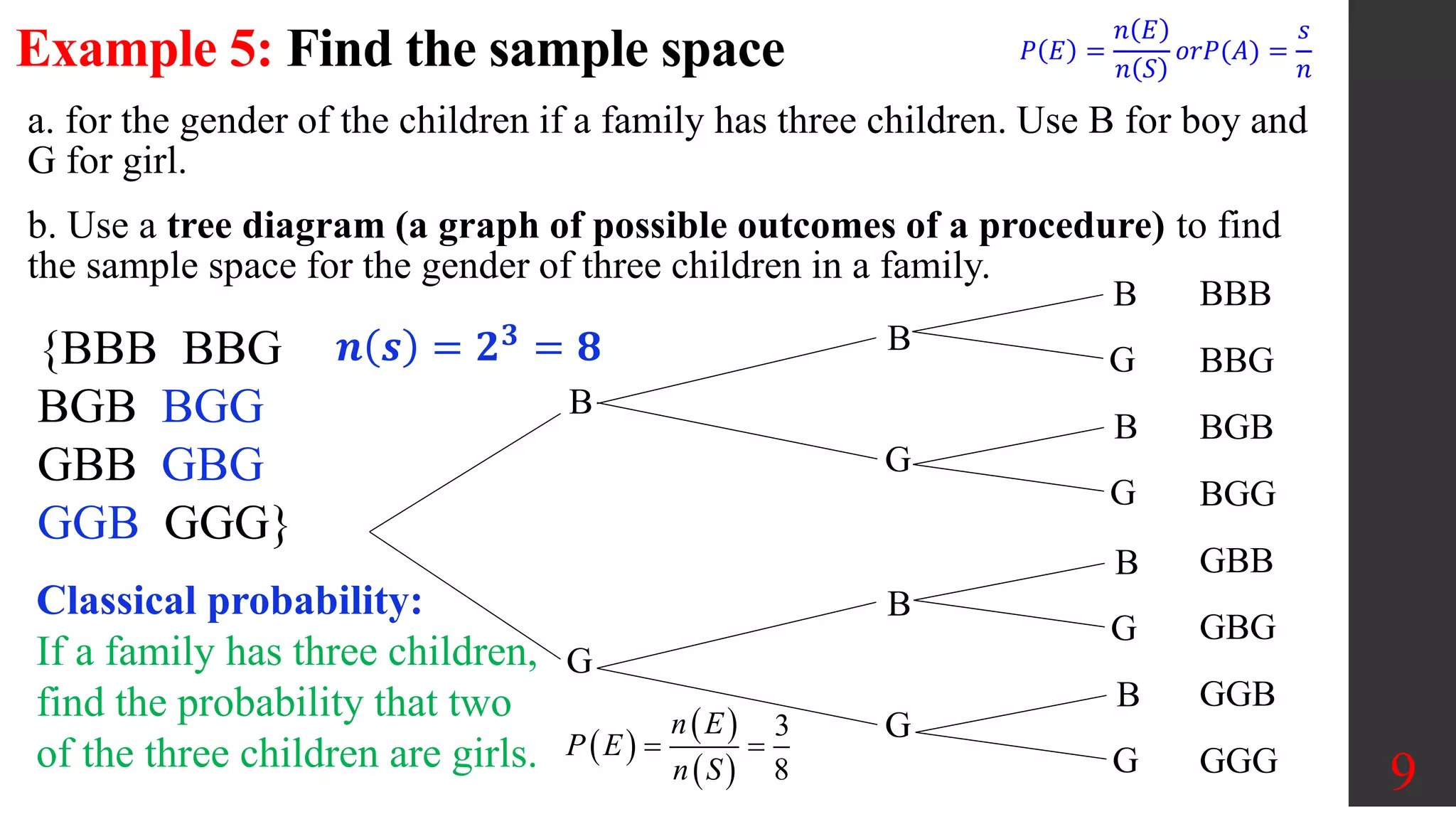
Chapter 4 of the document covers fundamental concepts of probability, including definitions of events, sample spaces, and various rules for calculating probabilities. It discusses approaches to finding probabilities such as classical, empirical, and subjective probability, as well as the law of large numbers and complementary events. Examples illustrate how to apply counting rules, calculate probabilities of simple and compound events, and explore the significance of results in probability experiments.