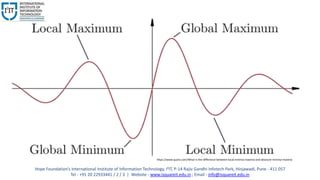
The document discusses maxima and minima of functions of two independent variables. It defines a relative minimum or maximum point of a function f(x,y) and explains how to determine the stationary points by simultaneously solving the partial derivatives of f with respect to x and y. The working rule outlined finds the extreme values by checking the signs of the second order partial derivatives at the stationary points. An example of finding the maxima of f(x,y)=x^2+y^2+12x+22y is provided to illustrate the process.