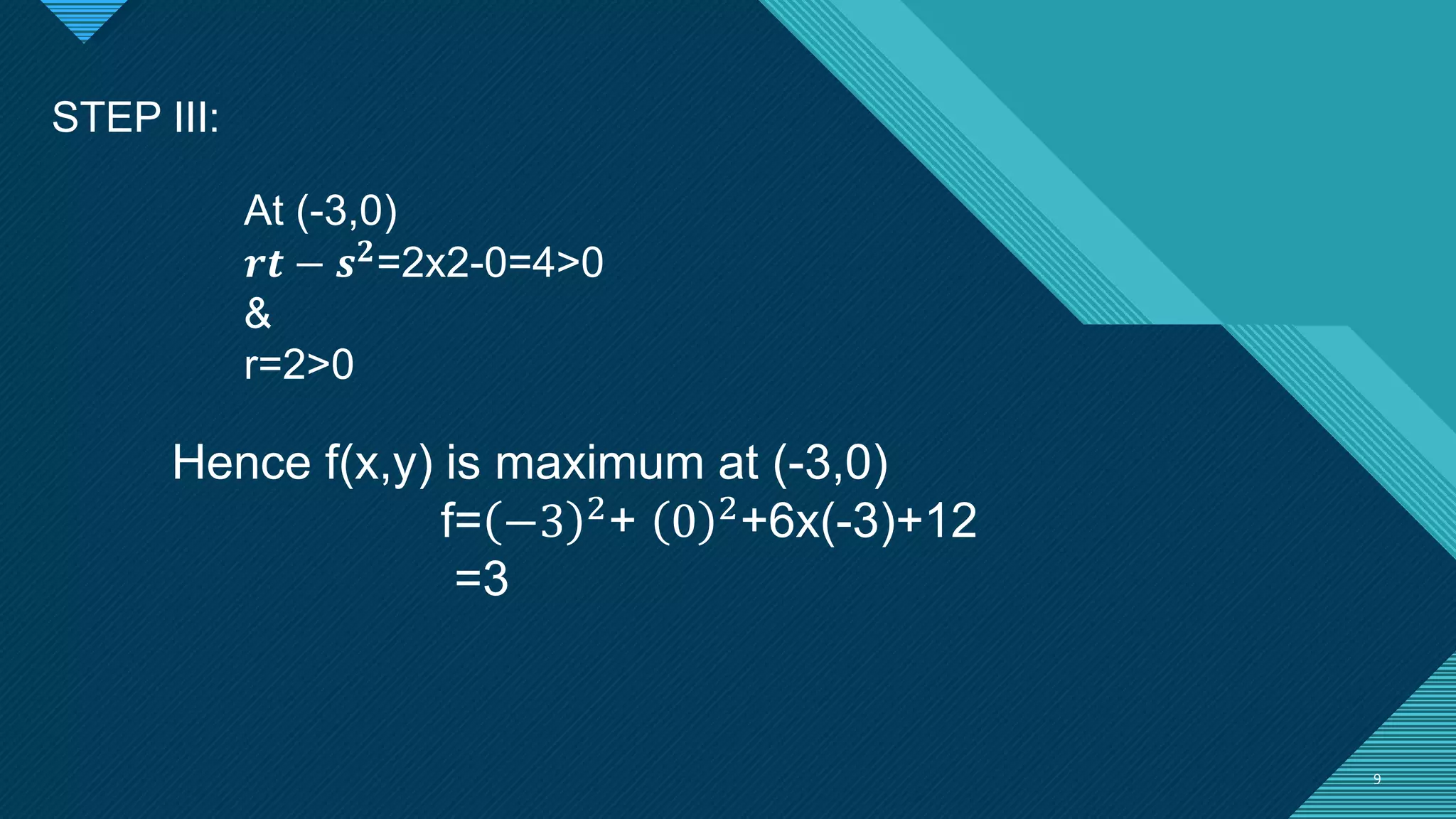This document discusses maxima and minima of functions of two independent variables. It provides the definitions of a relative minimum/maximum point as one where the function value at that point is less than or equal to/greater than or equal to the value at neighboring points. It describes stationary points as those where the function is maximum or minimum, and extreme values as the function values at stationary points. A working rule is given to determine maxima and minima, involving taking partial derivatives and checking signs of second-order derivatives. An example finds the maximum of the function f(x,y)=x^2+y^2+6x+12 at the stationary point (-3,0), with maximum value of 3.

1. Click to edit Master title style
1
MAXIMA AND MINIMA
P r e s e n t e d B y :
K a v e r i H a r i s h B a b u
2 0 G 2 1 A 0 5 7 3

2. Click to edit Master title style
2
MaximaandMinimaofFunctionsofTwoIndependentVariables
2
• Let f(x,y) be a function of two
independent variables x and y, which
is continuous for all values of x and
y in the neighborhood of (a,b) i.e.
(a+h,b+k) be a point in its
neighborhood which lies inside the
region R.

3. Click to edit Master title style
3 3
• The point (a,b) is called a point of relative
minimum, if f(a,b) ≤ f(a+h,b+k) for all h,k
Then f(a,b) is called the relative minimum value.
• The point (a,b) is called a point of relative
maximum, if f(a,b) ≥ f(a+h,b+k) for all h,k
Then f(a,b) is called the relative minimum value.

4. Click to edit Master title style
4 4
•Stationary point: The point at which function
is either maximum or minimum is known as
stationary point.
•Extreme Value: The value of the function at
stationary point is known as extreme value of
the function.

5. Click to edit Master title style
5
Working Rule
5
To determine the maxima and minima (extreme values) of a function f (x, y)
Step I : Solve
𝜕𝑓
𝜕𝑥
=0 &
𝜕𝑓
𝜕𝑦
=0 simultaneously for x and y
Step II: Obtain the values of
r=
𝜕2𝑓
𝜕𝑥2, s=
𝜕2𝑓
𝜕𝑦2, t=
𝜕2𝑓
𝜕𝑧2

6. Click to edit Master title style
6
.
6
•Step III:
1) If 𝒓𝒕 − 𝒔𝟐
> 0 & r < 0 at (a,b) , then f(x,y) is maximum at
(a,b) & maximum value of the function is f (a,b).
2) If 𝒓𝒕 − 𝒔𝟐 > 0 & r > 0 at (a,b) , then f(x,y) is maximum at
(a,b) & maximum value of the function is f (a,b).
3) If 𝒓𝒕 − 𝒔𝟐 < 0 at (a,b) , then f (x,y) is neither maximum nor
minimum at (a,b) .Such point is called Saddle Point.
4) If 𝒓𝒕 − 𝒔𝟐 < 0 at (a,b) , then no conclusion can be made
about the extreme values of f (x,y) & further investigation is
required.

7. Click to edit Master title style
7 7
Example 1
Q.1 Discuss the maxima and Minima of the function 𝑥2 + 𝑦2 + 6𝑥 + 12
Answer: f(x,y)= 𝑥2 + 𝑦2 + 6𝑥 + 12
Step 1: For extreme values
𝝏𝒇
𝝏𝒙
= 0
⇒ 2x+6=0, 2(x+3)=0
x = -3
&
𝝏𝒇
𝝏𝒚
= 0
⇒ 2y=0, y=0

8. Click to edit Master title style
8 8
Therefore stationary point is (-3,0)
STEP II:
r=
𝜕2𝑓
𝜕𝑥2=2,
s=
𝜕2𝑓
𝜕𝑦2=0,
t=
𝜕2𝑓
𝜕𝑧2=2.

9. Click to edit Master title style
9 9
STEP III:
At (-3,0)
𝒓𝒕 − 𝒔𝟐
=2x2-0=4>0
&
r=2>0
Hence f(x,y) is maximum at (-3,0)
f= −3 2
+ 0 2
+6x(-3)+12
=3

10. Click to edit Master title style
1010