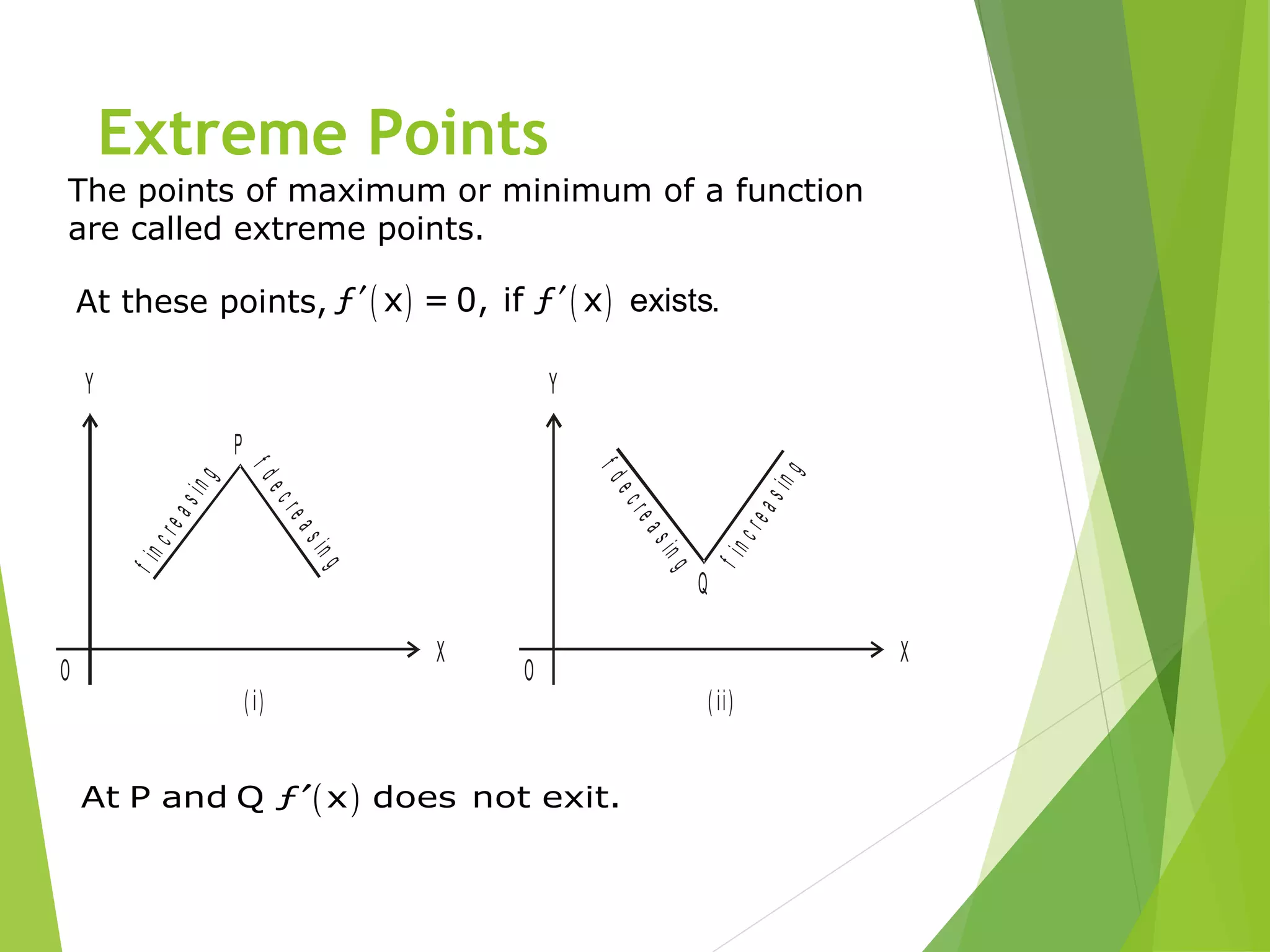
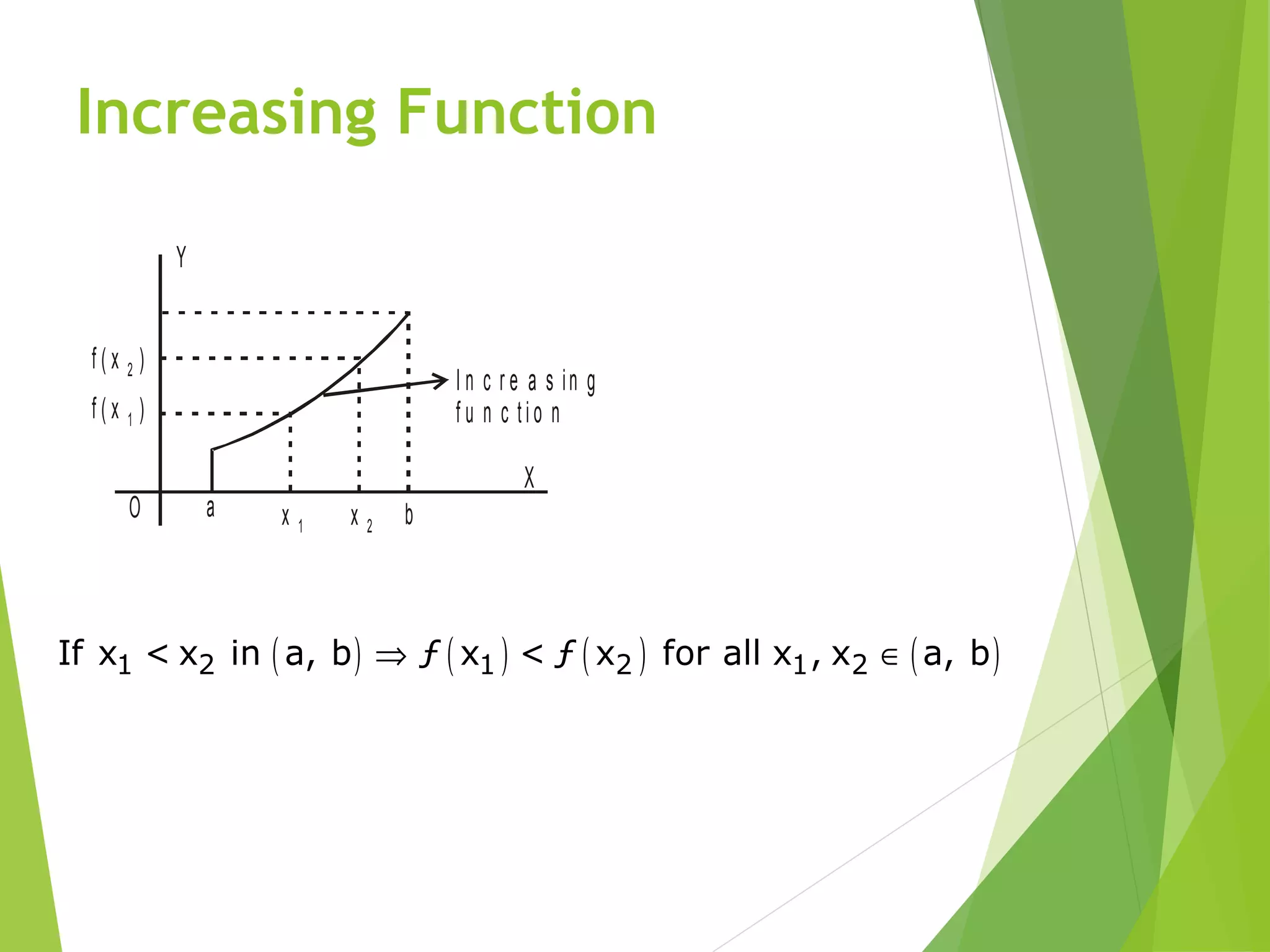
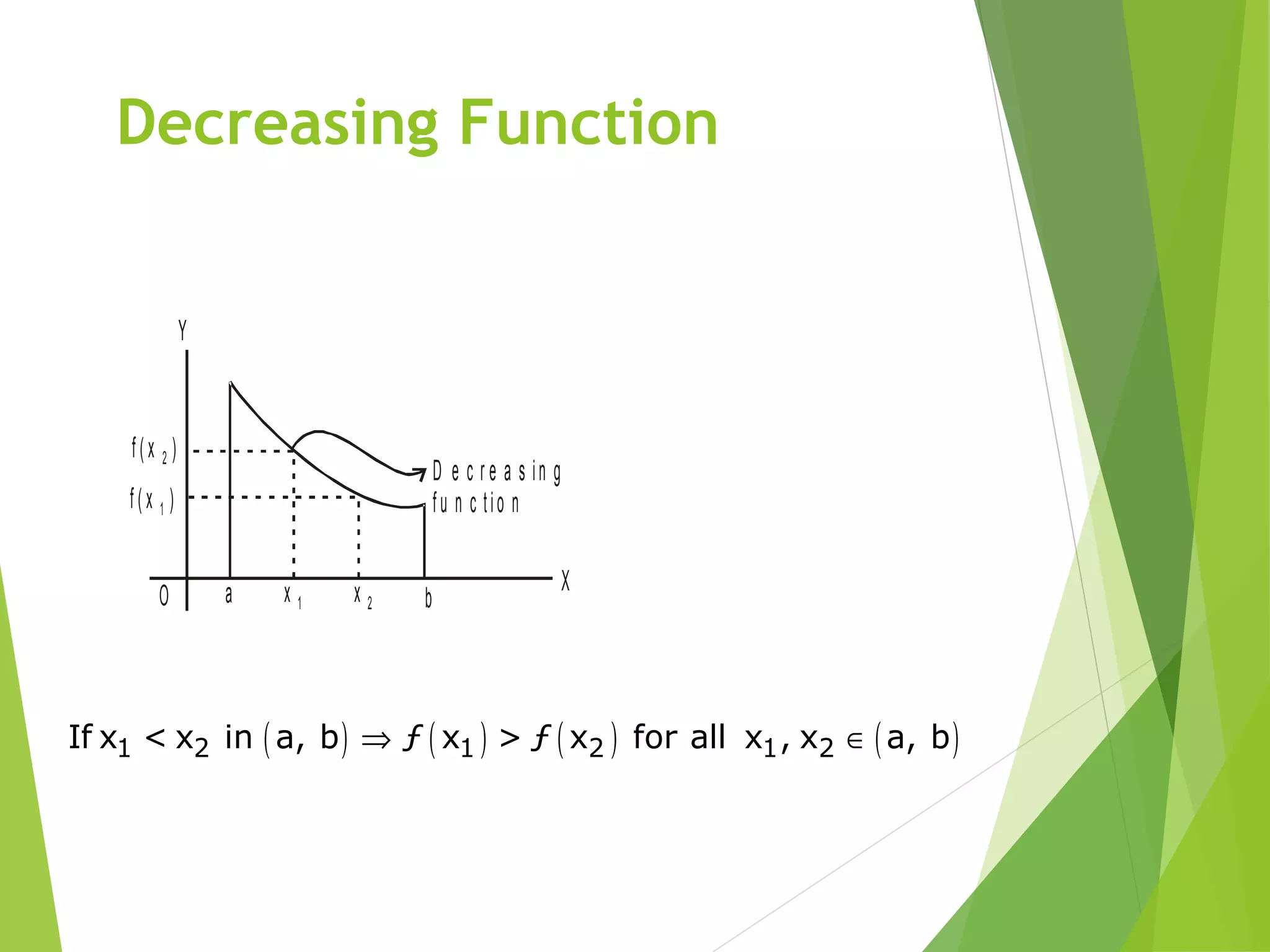
This document provides an introduction to applying derivatives, including finding maximum and minimum values of functions. It discusses increasing and decreasing functions, using the derivative to determine if a function is increasing or decreasing, and the relationship between the sign of the derivative and the tangent line slope. Extreme and critical points are defined. Two theorems are presented for determining if a point is a maximum or minimum based on the behavior of the function and its derivative around that point. An example problem finds the intervals where a sample function is increasing and decreasing. The objectives are to understand these derivative applications and concepts.

1. Welcome
To Presentation

2. Application of
Derivatives

3. Session Objectives
 Increasing and Decreasing Functions
 Use of Derivative
 Maximum and Minimum
 Extreme and Critical points
 Theorem 1 and 2
 Greatest and Least Values

4. I n c r e a s in g
f u n c ti o n
a x 1 bx 2
X
Y
f ( x 1 )
f ( x 2 )
O
Increasing Function
( ) ( ) ( ) ( )1 2 1 2 1 2If x < x in a, b ƒ x < ƒ x for all x , x a, b⇒ ∈

5. Decreasing Function
D e c r e a s in g
fu n c tio n
a x 1 bx 2
X
Y
f (x 1 )
f (x 2 )
O
( ) ( ) ( ) ( )1 2 1 2 1 2If x < x in a, b ƒ x > ƒ x for all x , x a, b⇒ ∈

6. Use of Derivative
( )(i) If ƒ x >0 for all x (a, b) f(x) is increasing on (a,b).′ ∈ ⇔
( )(ii) If ƒ x <0 for all x (a, b) f(x) is decresing on (a,b).′ ∈ ⇔

7. Use of Derivative (Con.)
[ ]As tanθ>0 for 0 <θ<90°
( )
dy
ƒ x 0
dx
′⇒ = > for all x in (a, b).
Y = f(x)
T
X
Y
O T' a b
Figure 1
P
θ

8. Use of Derivative (Con.)
θ
Figure 2 T'
X
Y
T a
bP
O
[ ]As tanθ <0 for 90°<θ<180°
( )
dy
ƒ x 0
dx
′⇒ = < for all x in (a, b).

9. For the function f(x) = 2x3
– 8x2
+ 10x +
5,
find the intervals where
(a)f(x) is increasing
(b) f(x) is decreasing
Example-1

10. Solution
3 2ƒ(x)=2x - 8x +10x +5
2
ƒ (x)= 6x -16x +10′∴
2
=2(3x - 8x +5)
=2(3x - 5)(x -1)
ƒ (x)= 0 2(3x - 5)(x -1)= 0′ ⇒
5
x = ,1
3
∴

11. Solution Cont.
5
For 1< x < , ƒ (x) is negative
3
′
5
For x > ,ƒ (x) is positive
3
′
For x < 1, is positive.ƒ (x)=3(3x - 5)(x -1)′
ƒ(x)∴ is increasing for x < 1 and
5
x >
3
and it decreases for 5
1< x <
3

12. Maximum and Minimum

13. Maximum and Minimum
The point a is called the point of maximum of the function f(x).
In the figure, y = f(x) has maximum values at Q and S.
( ) ( )ƒ a > ƒ a+δIf and ( ) ( )ƒ a > ƒ a-δ for all small values of δ.
The point b is called the point of minimum of the function f(x).
In the figure, y = f(x) has minimum values at R and T.
( ) ( )ƒ b < ƒ b+δIf and ( ) ( )ƒ b < ƒ b-δ for all small values of δ.
Let ( )y = ƒ x be a function

14. Extreme Points
The points of maximum or minimum of a function
are called extreme points.
At these points, ( ) ( )ƒ x = 0, if ƒ x exists.′ ′
X
Y
O
( i)
P
fincreasing
fdecreasing
X
Y
O
( ii)
Q
fincreasing
fdecreasing
( )At P and Q ƒ x does not exit.′

15. Critical Points
The points at which or at which
does not exist are called critical points.
( )ƒ x = 0′ ( )ƒ x′
A point of extremum must be one of the critical
points, however, there may exist a critical point,
which is not a point of extremum.

16. Theorem - 1
Let the function be continuous in some
interval containing x0 .
( )y = ƒ x
( )ƒ x >0′ ( )ƒ x <0′(i) If when x < x0 and When
x > x0 then f(x) has maximum value at x = x0
( )ƒ x <0′ ( )ƒ x >0′(ii) If when x < x0 and When
x > x0 ,then f(x) has minimum value at x = x0

17. Theorem - 2
If x0 be a point in the interval in which y = f(x) is
defined and if ( ) ( )0 0ƒ x =0 and ƒ x 0′ ′′ ≠
( ) ( ) ( )if0 0i ƒ x is a maximum ƒ x <0′′
( ) ( ) ( )if0 0ii ƒ x is a minimum ƒ x >0′′

18. Thank you