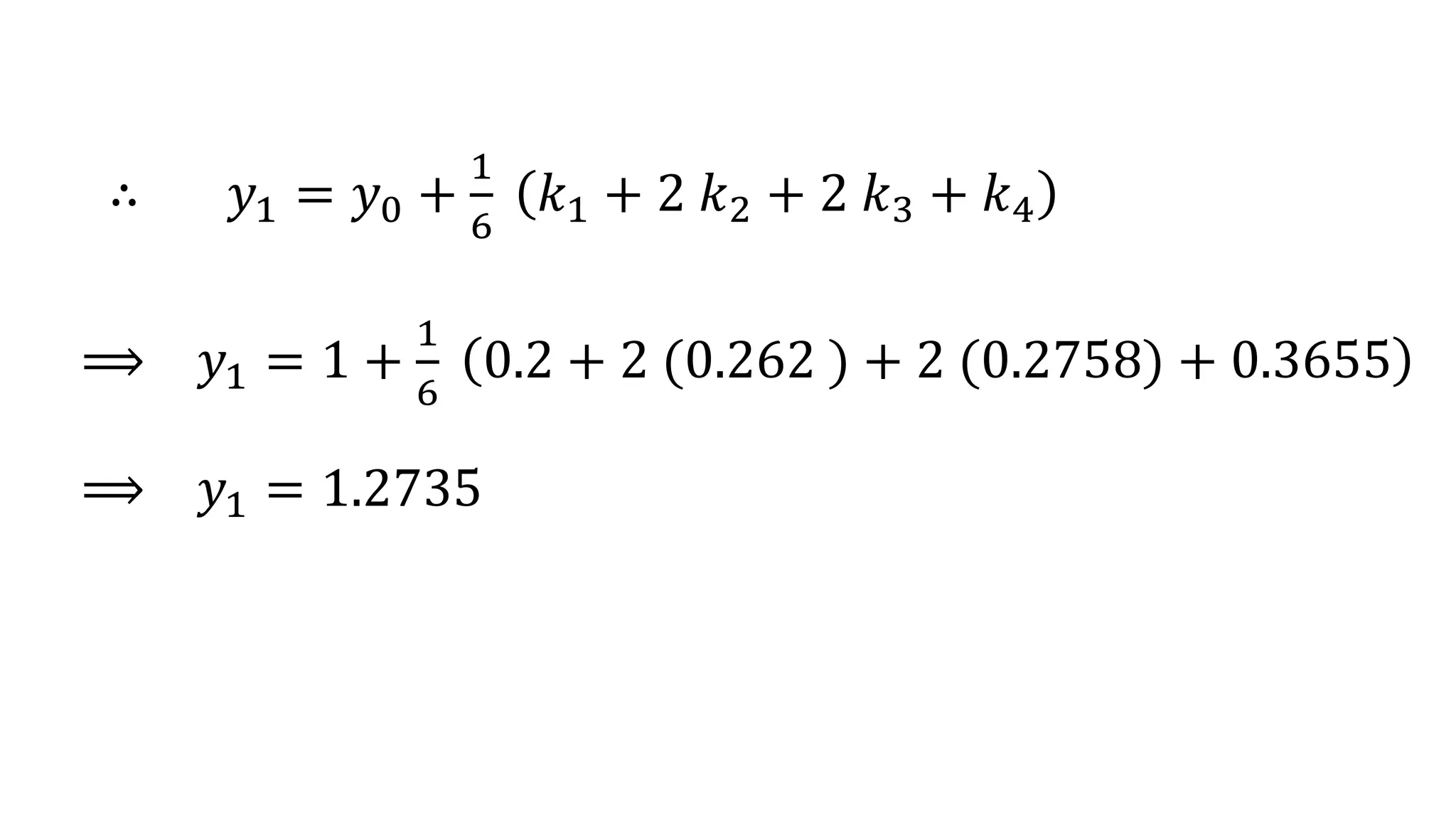The document describes the fourth-order Runge-Kutta method for solving first-order ordinary differential equations given an initial condition. It details the calculation steps to approximate the solution, including how to determine intermediate values k1, k2, k3, and k4. An example is provided to illustrate the method, solving the equation dy/dx = x + y^2 with specified initial conditions.

1. Runge – Kutta Method of 4th Order
21UMT2T462: Numerical Analysis
Dr. Soya Mathew
Assistant Professor in Mathematics
Department of Physical Sciences
Kristu Jayanti College (Autonomous)
Bengaluru – 560077, India

2. Runge – Kutta Method
Consider first order ordinary differential equations of the form
𝑑𝑦
𝑑𝑥
= 𝑓 𝑥, 𝑦 … … 1
with initial condition 𝑦 = 𝑦0 when 𝑥 = 𝑥0.

3. Runge – Kutta Method
The approximate solution of the equation at 𝑥1 = 𝑥0 + ℎ is given by
𝑦1 = 𝑦0 +
1
6
𝑘1 + 2 𝑘2 + 2 𝑘3 + 𝑘4
Where 𝑘1 = ℎ 𝑓(𝑥0, 𝑦0) , 𝑘2 = ℎ 𝑓(𝑥0 +
ℎ
2
, 𝑦0 +
𝑘1
2
)
𝑘3 = ℎ 𝑓(𝑥0 +
ℎ
2
, 𝑦0 +
𝑘2
2
), 𝑘4 = ℎ 𝑓(𝑥0 + ℎ, 𝑦0 + 𝑘3)
This solution 𝑦1 is called fourth order Runga – Kutta Solution or Runga – Kutta
Solution.

4. Runge – Kutta Method
After finding the first approximation, the approximate solution at
𝑥2 = 𝑥1 + ℎ can be obtained by
𝑦2 = 𝑦1 +
1
6
𝑘1 + 2 𝑘2 + 2 𝑘3 + 𝑘4
Where 𝑘1 = ℎ 𝑓(𝑥1, 𝑦1) , 𝑘2 = ℎ 𝑓(𝑥1 +
ℎ
2
, 𝑦1 +
𝑘1
2
)
𝑘3 = ℎ 𝑓(𝑥1 +
ℎ
2
, 𝑦1 +
𝑘2
2
), 𝑘4 = ℎ 𝑓(𝑥1 + ℎ, 𝑦1 + 𝑘3)

5. Runge – Kutta Method
In general,
𝑦𝑛+1 = 𝑦𝑛 +
1
6
𝑘1 + 2 𝑘2 + 2 𝑘3 + 𝑘4
Where 𝑘1 = ℎ 𝑓(𝑥𝑛, 𝑦𝑛) , 𝑘2 = ℎ 𝑓(𝑥𝑛 +
ℎ
2
, 𝑦𝑛 +
𝑘1
2
)
𝑘3 = ℎ 𝑓(𝑥𝑛 +
ℎ
2
, 𝑦𝑛 +
𝑘2
2
), 𝑘4 = ℎ 𝑓(𝑥𝑛 + ℎ, 𝑦𝑛 + 𝑘3)

6. Problem: Solve
𝒅𝒚
𝒅𝒙
= 𝒙 + 𝒚𝟐
, with initial condition 𝒚 = 𝟏 when
𝒙 = 𝟎, for 𝒙 = 𝟎. 𝟐 𝟎. 𝟐 𝟎. 𝟒 using Runga – Kutta Method
Solution:
Here 𝑓 𝑥, 𝑦 = 𝑥 + 𝑦2
, 𝑥0 = 0, 𝑦0 = 1 and ℎ = 0.2
First approximation to the solution at 𝑥1 = 0.2 is given by
𝑦1 = 𝑦0 +
1
6
𝑘1 + 2 𝑘2 + 2 𝑘3 + 𝑘4
Where 𝑘1 = ℎ 𝑓 𝑥0, 𝑦0 = 0.2 0 + 12
= 0.2

7. 𝑘2 = ℎ 𝑓 𝑥0 +
ℎ
2
, 𝑦0 +
𝑘1
2
⟹ 𝑘2 = 0.2 𝑓 0 +
0.2
2
, 1 +
0.2
2
⟹ 𝑘2 = 0.2 0.1, 1.1
⟹ 𝑘2 = 0.2 0.1 + 1.12
= 0.262

8. 𝑘3 = ℎ 𝑓(𝑥0 +
ℎ
2
, 𝑦0 +
𝑘2
2
)
⟹ 𝑘3 = 0.2 𝑓 0 +
0.2
2
, 1 +
0.262
2
⟹ 𝑘3 = 0.2 0.1, 1.131
⟹ 𝑘3 = 0.2 0.1 + 1.1312
= 0.2758

9. 𝑘4 = ℎ 𝑓(𝑥0 + ℎ, 𝑦0 + 𝑘3)
⟹ 𝑘4 = 0.2 𝑓 0 + 0.2, 1 + 0.2758
⟹ 𝑘4 = 0.2 0.2, 1.2758
⟹ 𝑘4 = 0.2 0.2 + 1.27582
= 0.3655

10. ∴ 𝑦1 = 𝑦0 +
1
6
𝑘1 + 2 𝑘2 + 2 𝑘3 + 𝑘4
⟹ 𝑦1 = 1 +
1
6
0.2 + 2 (0.262 ) + 2 (0.2758) + 0.3655
⟹ 𝑦1 = 1.2735

11. Second approximation to the solution at 𝑥2 = 0.4 is given by
𝑦2 = 𝑦1 +
1
6
𝑘1 + 2 𝑘2 + 2 𝑘3 + 𝑘4
Where 𝑘1 = ℎ 𝑓 𝑥1, 𝑦1 = 0.2 0.2 + 1.27352
= 0.3644
𝑘2 = ℎ 𝑓 𝑥1 +
ℎ
2
, 𝑦1 +
𝑘1
2
⟹ 𝑘2 = 0.2 𝑓 0.2 +
0.2
2
, 1.2735 +
0.3644
2
⟹ 𝑘2 = 0.2 0.3, 1.1822

12. ⟹ 𝑘2 = 0.2 0.3 + 1.45572
= 0.4838
𝑘3 = ℎ 𝑓(𝑥1 +
ℎ
2
, 𝑦1 +
𝑘2
2
)
⟹ 𝑘3 = 0.2 𝑓 0.2 +
0.2
2
, 1.2735 +
0.4838
2
⟹ 𝑘3 = 0.2 0.3, 1.5154
⟹ 𝑘3 = 0.2 0.3 + 1.51542
= 0.5193

13. 𝑘4 = ℎ 𝑓(𝑥1 + ℎ, 𝑦1 + 𝑘3)
⟹ 𝑘4 = 0.2 𝑓 0.2 + 0.2, 1.2735 + 0.5193
⟹ 𝑘4 = 0.2 0.4, 1.7928
⟹ 𝑘4 = 0.2 0.4 + 1.79282
= 0.7228

14. ∴ 𝑦2 = 𝑦1 +
1
6
𝑘1 + 2 𝑘2 + 2 𝑘3 + 𝑘4
⟹ 𝑦2 = 1.2735 +
1
6
0.3644 + 2 (0.4838 ) + 2 (0.5193) + 0.7228
⟹ 𝑦2 = 1.7891
Thus 𝑦2 = 𝑦 0.4 = 1.7891 is the approximate solution of 𝑦
at 𝑥 = 0.4.