Downloaded 34 times
Uploaded bygandhinagar
Eighan values and diagonalization
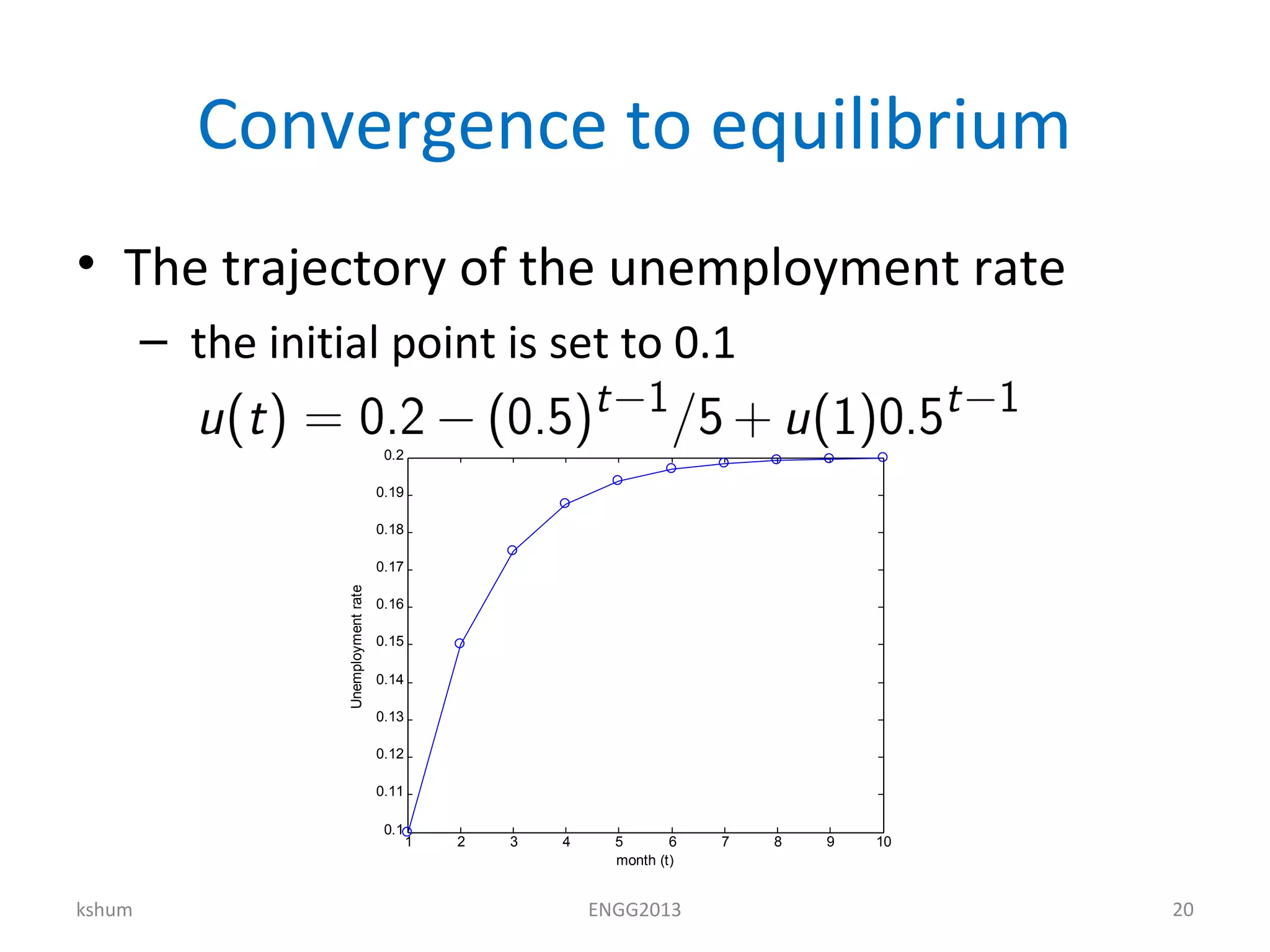
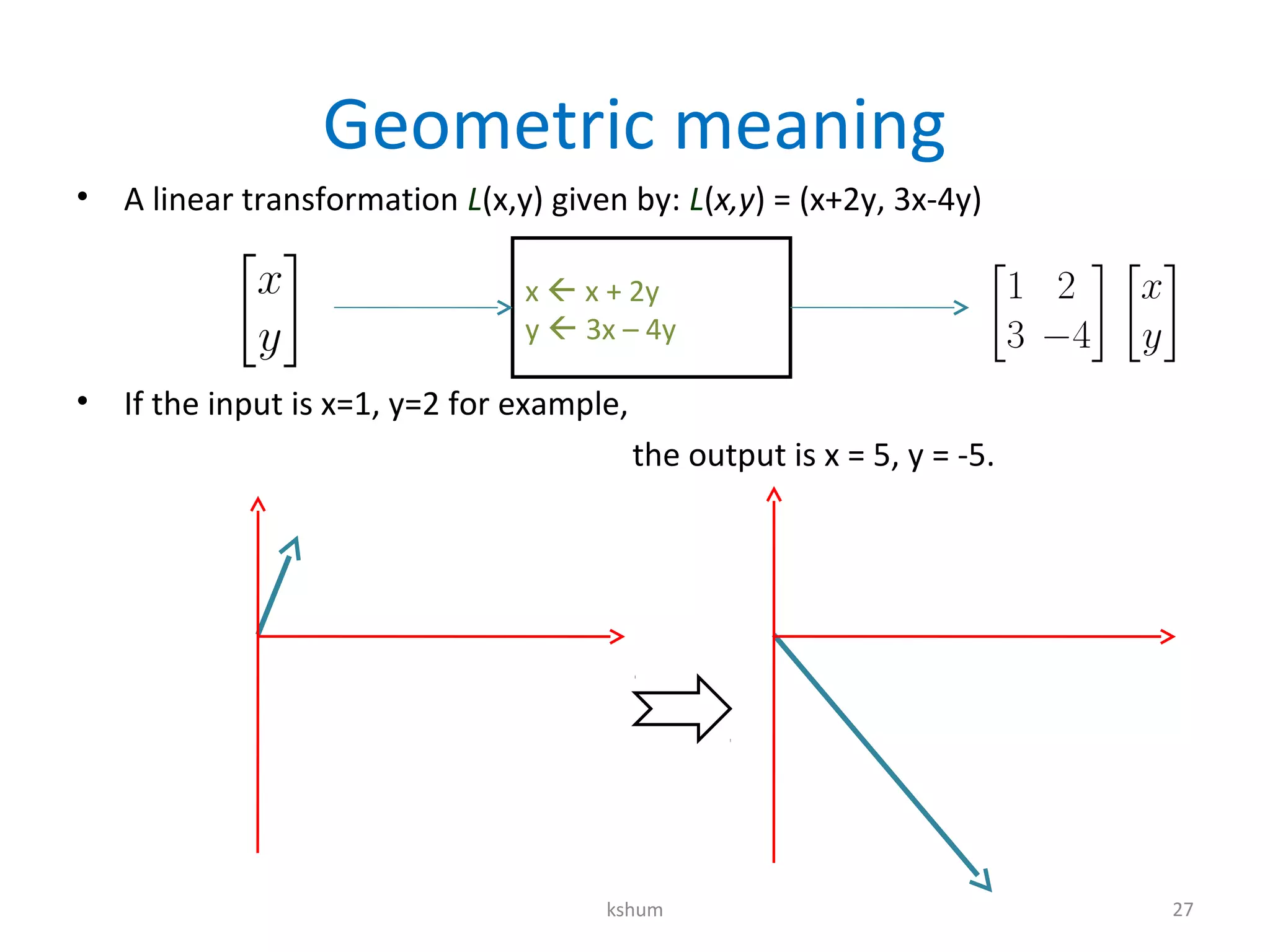
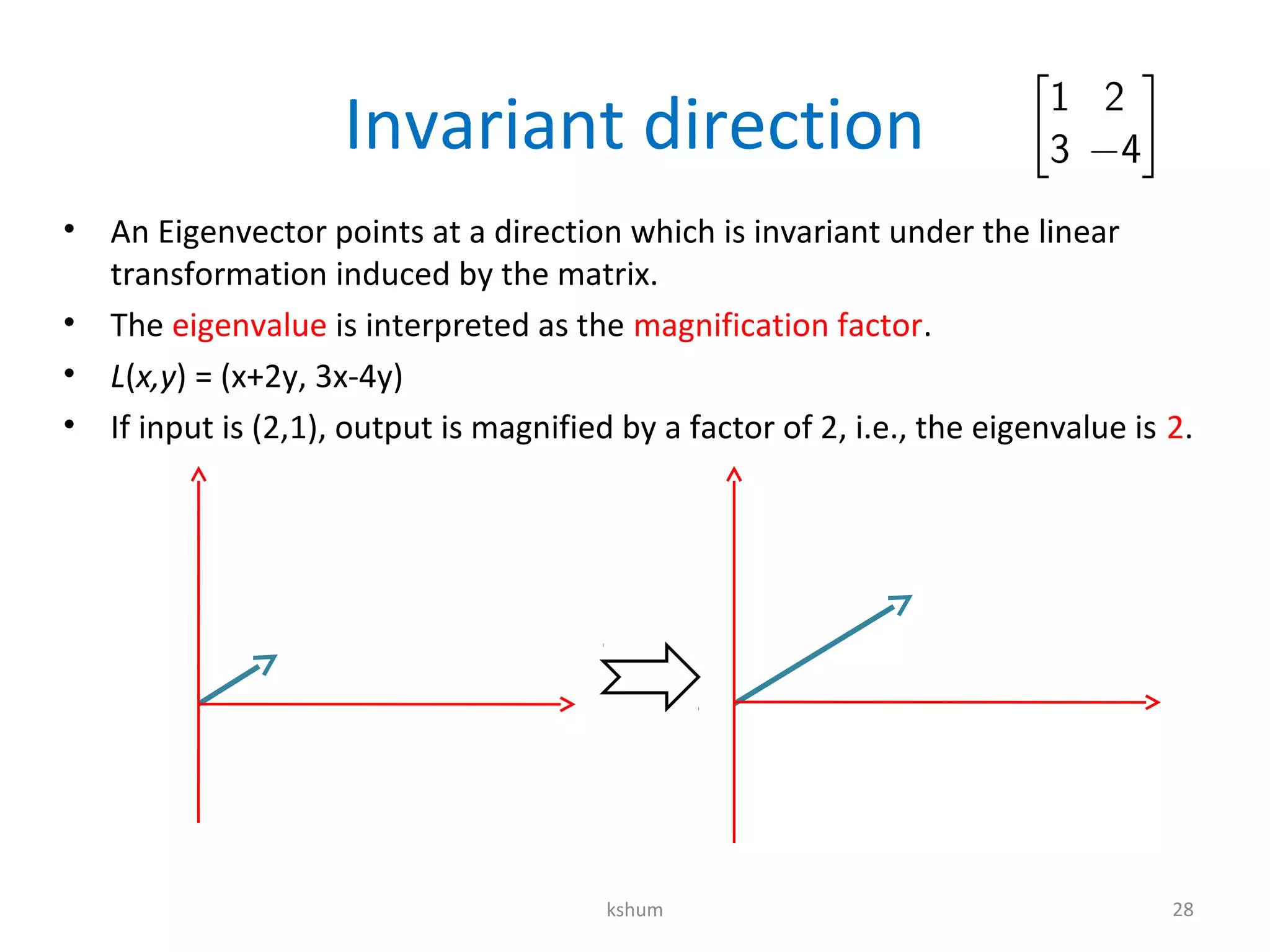
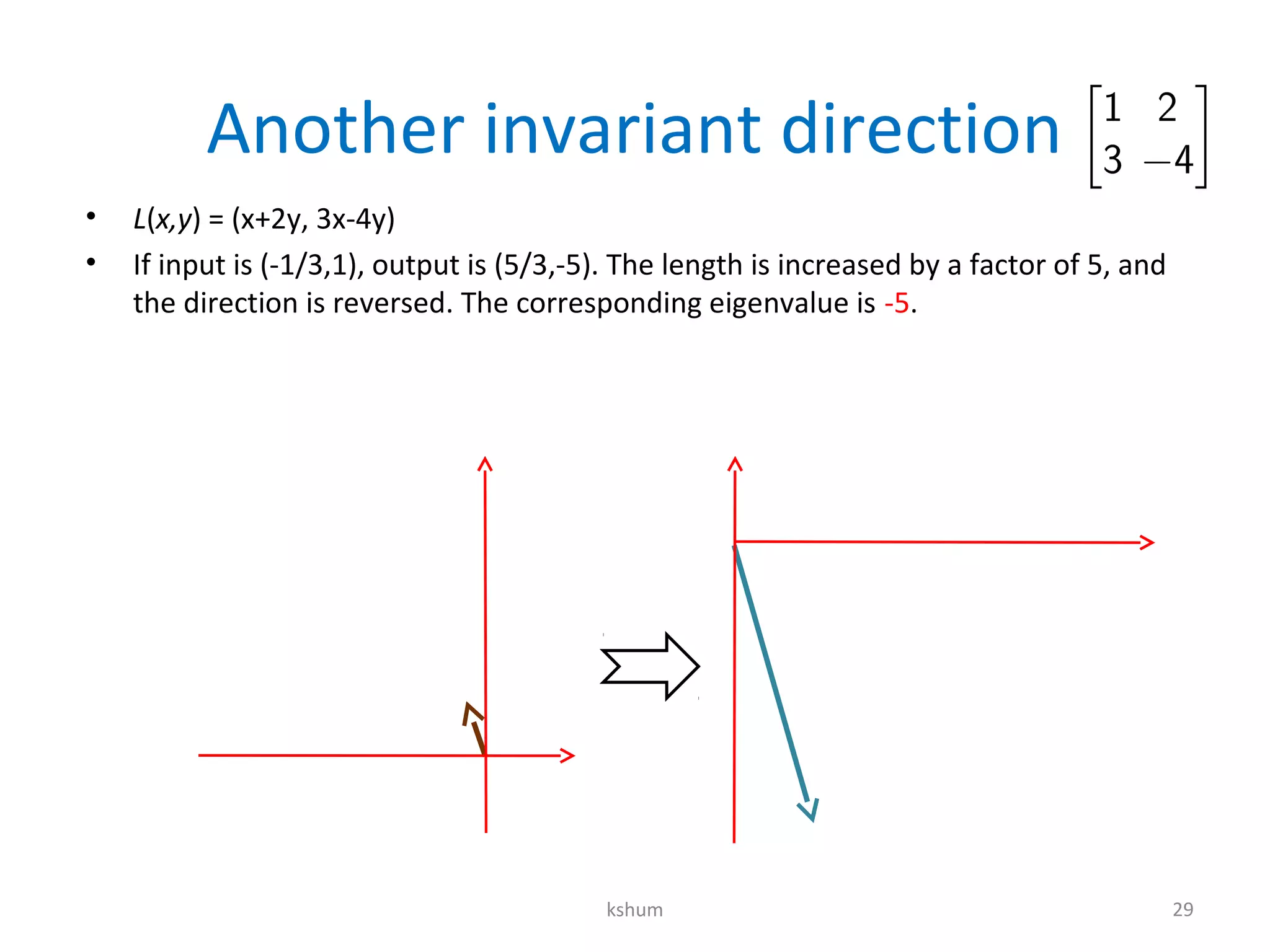
This document contains notes on diagonalization, eigenvalues, and eigenvectors. It discusses how to solve recurrence relations using matrix multiplication and raises matrices to arbitrary powers by diagonalizing them. Diagonalization involves finding an invertible matrix P such that P-1MP is a diagonal matrix D. The columns of P are the eigenvectors of M, and the entries of D are the corresponding eigenvalues. This allows raising M to a power to be reduced to raising the simpler diagonal matrix D to the same power.
More Related Content
Similar to Eighan values and diagonalization
Eighan values and diagonalization
- 1. ENGG2013 Unit 17 Diagonalization Eigenvectorand eigenvalue Mar, 2011.
- 2.
- 3. Q6 in midterm •u(t): unemployment rate in the t-th month. • e(t)= 1-u(t) • The unemployment rate in the next month is given by a matrix multiplication • Equilibrium: Solve kshum ENGG2013 3 Unemployment rate at equilibrium = 0.2
- 4.
- 5. If stable, howfast does it converge to the equilibrium point? kshum ENGG2013 5 0.2 0.2 Fast convergenceSlow convergence
- 6. Question • Suppose thatthe initial unemployment rate at the first month is x(1), (for example x(1)=0.25), and suppose that the unemployment evolves by matrix multiplication Find an analytic expression for x(t), for all t. kshum ENGG2013 6
- 7.
- 8. How to count? •Count the number of binary strings of length n with no consecutive ones. kshum ENGG2013 8
- 9. SOLVING RECURRENCE RELATION kshumENGG2013 9
- 10. Fibonacci numbers • F1= 1 • F2 = 1 • For n > 2, Fn = Fn-1+Fn-2. • The Fibonacci numbers are – 1,1,3,5,8,13,21,34,55,89,144 kshum ENGG2013 10 http://en.wik
- 11. A matrix formulation •Define a vector • Initial vector • Find the recurrence relation in matrix form kshum ENGG2013 11
- 12. A general question •Given initial condition and for t ≥ 2 Find v(t) for all t. kshum ENGG2013 12
- 13. Matrix power • Needto raise a matrix to a very high power kshum ENGG2013 13
- 14. A trivial specialcase • Diagonal matrix • The solution is easy to find • Raising a diagonal matrix to the power t is easy. kshum ENGG2013 14
- 15. Decoupled equations • Whenthe equation is diagonal, we have two separate equation, each in one variable kshum ENGG2013 15
- 16.
- 17. Problem reduction • Asquare matrix M is called diagonalizable if we can find an invertible matrix, say P, such that the product P–1 M P is a diagonal matrix. • A diagonalizable matrix can be raised to a high power easily. – Suppose that P–1 M P = D, D diagonal. – M = PD P–1 . – Mn = (PD P–1 ) (PD P–1 ) (PD P–1 ) … (PD P–1 ) = PDn P–1 . kshum ENGG2013 17
- 18. Example of diagonalizablematrix • Let • A is diagonalizable because we can find a matrix such that kshum ENGG2013 18
- 19. Now we knowhow fast it converges to 0.2 • The matrix can be diagonalized kshum ENGG2013 19
- 20. Convergence to equilibrium •The trajectory of the unemployment rate – the initial point is set to 0.1 kshum ENGG2013 20 1 2 3 4 5 6 7 8 9 10 0.1 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.19 0.2 month (t) Unemploymentrate
- 21. EIGENVECTOR AND EIGENVALUE kshumENGG2013 21
- 22. How to diagonalize? •How to determine whether a matrix M is diagonalizable? • How to find a matrix P which diagonalizes a matrix M? kshum ENGG2013 22
- 23. From diagonalization to eigenvector •By definition a matrix M is diagonalizable if P–1 M P = D for some invertible matrix P, and diagonal matrix D. or equivalently, kshum ENGG2013 23
- 24. The columns ofP are special • Suppose that kshum ENGG2013 24
- 25. Definition • Given asquare matrix A, a non-zero vector v is called an eigenvector of A, if we an find a real number λ (which may be zero), such that • This number λ is called an eigenvalue of A, corresponding to the eigenvector v. kshum ENGG2013 25 Matrix-vector product Scalar product of a vector
- 26. Important notes • Ifv is an eigenvector of A with eigenvalue λ, then any non-zero scalar multiple of v also satisfies the definition of eigenvector. kshum ENGG2013 26 k ≠ 0
- 27. Geometric meaning • Alinear transformation L(x,y) given by: L(x,y) = (x+2y, 3x-4y) • If the input is x=1, y=2 for example, the output is x = 5, y = -5. kshum 27 x x + 2y y 3x – 4y
- 28. Invariant direction • AnEigenvector points at a direction which is invariant under the linear transformation induced by the matrix. • The eigenvalue is interpreted as the magnification factor. • L(x,y) = (x+2y, 3x-4y) • If input is (2,1), output is magnified by a factor of 2, i.e., the eigenvalue is 2. kshum 28
- 29. Another invariant direction •L(x,y) = (x+2y, 3x-4y) • If input is (-1/3,1), output is (5/3,-5). The length is increased by a factor of 5, and the direction is reversed. The corresponding eigenvalue is -5. kshum 29
- 30. Eigenvalue and eigenvectorof First eigenvalue = 2, with eigenvector where k is any nonzero real number. Second eigenvalue = -5, with eigenvector where k is any nonzero real number. kshum ENGG2013 30
- 31. Summary • Motivation: wantto solve recurrence relations. • Formulation using matrix multiplication • Need to raise a matrix to an arbitrary power • Raising a matrix to some power can be easily done if the matrix is diagonalizable. • Diagonalization can be done by eigenvalue and eigenvector. kshum ENGG2013 31
Editor's Notes
- #16 \begin{bmatrix} x(t+1)\\ y(t+1) \end{bmatrix}=\begin{bmatrix} a & 0\\ 0& b \end{bmatrix}\begin{bmatrix} x(t)\\ y(t) \end{bmatrix}
- #19 \mathbf{A} = \begin{bmatrix} 0.9 & 0.4\\ 0.1 & 0.6 \end{bmatrix}
- #20 \begin{bmatrix} x(t+1)\\ y(t+1) \end{bmatrix} =\begin{bmatrix} 0.9 & 0.4\\ 0.1 & 0.6 \end{bmatrix}^t\begin{bmatrix} x(1)\\ y(1) \end{bmatrix}\\ = \begin{bmatrix} 4 &-1 \\ 1 &1 \end{bmatrix} \begin{bmatrix} 1 & 0\\ 0 & 0.5 \end{bmatrix}^t \begin{bmatrix} 4 &-1 \\ 1 &1 \end{bmatrix}^{-1}\begin{bmatrix} x(1)\\ y(1) \end{bmatrix}
- #21 u(t)=0.2 - (0.5)^{t-1}/5 + u(1) 0.5^{t-1}
- #25 \mathbf{P}=\begin{bmatrix} x_1 & x_2 & x_3\\ y_1 & y_2 & y_3\\ z_1 & z_2 & z_3 \end{bmatrix}