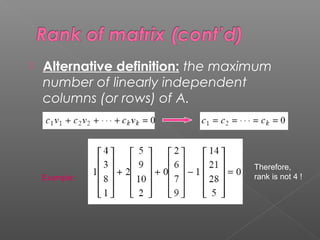
This document discusses several key linear algebra concepts: 1) A square matrix is diagonalizable if it can be transformed into a diagonal matrix through multiplication by an invertible matrix. Diagonalizable matrices can be easily raised to high powers. 2) Eigenvalues and eigenvectors are values and vectors that are unchanged by transformation by the matrix, up to a scaling factor for eigenvectors. 3) Orthogonal matrices preserve lengths and angles when multiplying vectors. The Cayley-Hamilton theorem states that every matrix satisfies its own characteristic equation.

1. Topic:
DIAGONALIZATION,
EIGEN VALUE,
EIGEN VECTOR,
ORTHOGONAL,
CAYLEY HAMILTON THEORM
By rajesh goswami

2.  DIAGONALIZATION
 EIGEN VALUE
 EIGEN VECTOR
 ORTHOGONAL
 CAYLEY HAMILTON THEOREM
kshumENGG2013 2

4.  A square matrix M is called
diagonalizable if we can find an
invertible matrix, say P, such that the
product P–1
M P is a diagonal matrix.
 A diagonalizable matrix can be raised to
a high power easily.
› Suppose that P–1
M P = D, D diagonal.
› M = PD P–1
.
› Mn
= (PD P–1
) (PD P–1
) (PD P–1
) … (PD P–1
)
= PDn
P–1
.
4

5.  Let
 A is diagonalizable because we can find
a matrix
such that
5

6.  By definition a matrix M is diagonalizable
if
P–1
M P = D
for some invertible matrix P, and diagonal
matrix D.
or equivalently,
6

7.  Suppose that
7

8.  Given a square matrix A, a non-zero
vector v is called an eigenvector of A, if
we an find a real number λ (which may
be zero), such that
 This number λ is called an eigen value of
A, corresponding to the eigenvector v.
8
Matrix-vector product Scalar product of a vector

9.  If v is an eigenvector of A with eigen
value λ, then any non-zero scalar
multiple of v also satisfies the definition of
eigenvector.
9
k ≠ 0

10. First eigenvalue = 2, with eigenvector
where k is any nonzero real number.
Second eigenvalue = -5, with eigenvector
where k is any nonzero real number.
10

12.  Matrix addition/subtraction
› Matrices must be of same size.
 Matrix multiplication
Condition: n = q
m x n q x p m x p

15. Example:

16. 2 x 2
3 x 3
n x n

17. diagonal matrix:

18.  The inverse A-1
of a matrix A has the
property:
AA-1
=A-1
A=I
 A-1
exists only if
 Terminology
› Singular matrix: A-1
does not exist
› Ill-conditioned matrix: A is close to being singular

19.  Properties of the inverse:

20.  The pseudo-inverse A+
of a matrix A
(could be non-square, e.g., m x n) is
given by:
 It can be shown that:

21.  Equal to the dimension of the largest
square sub-matrix of A that has a non-
zero determinant.
Example:
has rank 3

22.  Alternative definition: the maximum
number of linearly independent
columns (or rows) of A.
Therefore,
rank is not 4 !Example:

24. • A is orthogonal if:
• Notation:
Example:

25. • A is orthonormal if:
• Note that if A is orthonormal, it easy to find its inverse:
Property:

26. Diagonalize the matrix A = by means of an
orthogonal transformation.
Solution:-
Characteristic equation of A is
204
060
402
66,2,λ
0λ)16(6λ)λ)(2λ)(6(2
0
λ204
0λ60
40λ2
−=⇒
=−−−−−⇒
=
−
−
−
26
Example :-

27. I
 
 
 
  
     
     
     
          
⇒
∴
 
 ∴  
  
1
1 2
3
1
1
2
3
1 3
2
1 3
1 1 2 3 1
1 1
x
whenλ = -2,let X = x betheeigenvector
x
then (A +2 )X = 0
4 0 4 x 0
0 8 0 x = 0
4 0 4 x 0
4x + 4x = 0 ...(1)
8x = 0 ...(2)
4x +4x = 0 ...(3)
x =k ,x = 0,x = -k
1
X = k 0
-1
27

28. 2
2I
0
 
 
 
  
     
     
     
          
⇒ −
∴
1
2
3
1
2
3
1 3
1 3
1 3 2
2 2 3
x
whenλ = 6,let X = x betheeigenvector
x
then (A -6 )X =0
-4 0 4 x 0
0 0 x = 0
4 0 -4 x 0
4x +4x =0
4x -4x =0
x = x and x isarbitrary
x must be so chosen that X and X are orthogonal among th
.1
emselves
and also each is orthogonal with X
28

29.    
   
   
      
∴
∴
 
 
 
  
∴
2 3
3 1
3 2
3
1α
Let X = 0 and let X =β
1γ
Since X is orthogonal to X
α- γ = 0 ...(4)
X is orthogonal to X
α+ γ = 0 ...(5)
Solving (4)and(5), we getα = γ = 0 and β is arbitra ry.
0
Takingβ =1, X = 1
0
1 1 0
Modal matrix is M= 0 0 1
-1 1
 
 
 
  0
29

30.  
 
 
 
 
 
  
 
  
    
    
    
        
    
 
 
 
  
The normalised modal matrix is
1 1
0
2 2
N = 0 0 1
1 1
- 0
2 2
1 1
0 - 1 1
02 2 2 0 4 2 2
1 1
D =N'AN = 0 0 6 0 0 0 1
2 2
4 0 2 1 1
- 00 1 0
2 2
-2 0 0
D = 0 6 0 which is the required diagonal matrix
0 0 6
.
30

32. nnnn2n1n
n22221
n11211
a...aa
................
a...aa
a...aa
A
×












=

33.  
 
 
 
 
 
11 12 1n
21 22 2n
n1 n2 nn
φ(λ) = A - λI
a -λ a ... a
a a -λ ... a
=
... ... ... ...
a a ... a -λ
| A -λI|= 0

34. ⇒ n n-1 n-2
0 1 2 n
n n-1 n-2
0 1 2 n
We are to prove that
pλ +p λ +p λ +...+p = 0
p A +p A +p A +...+p I= 0 ...(1)
I
⇒
n-1 n-2 n-3 -1
0 1 2 n-1 n
-1 n-1 n-2 n-3
0 1 2 n-1
n
0 =p A +p A +p A +...+p +p A
1
A =- [p A +p A +p A +...+p I]
p

36. 









−
−−
−
211
121
112
tion)simplifica(on049λ6λλor
0
λ211
1λ21
11λ2
i.e.,0λIA
23
=−+−
=
−−
−−−
−−
=−
Example 1:-

37. 









−
−−
−−
=










−
−−
−










−
−−
−
=×=










−
−−
−
=










−
−−
−










−
−−
−
=
222121
212221
212222
211
121
112
655
565
556
655
565
556
211
121
112
211
121
112
23
2
AAA
A

38. ∴










−
−−
−−
222121
212221
212222










−
−−
−
655
565
556










−
−−
−
211
121
112










100
010
001
0
000
000
000
=











39. Now, pre – multiplying both sides of (1) by A-1
, we
have
A2
– 6A +9I – 4 A-1
= 0
=> 4 A-1
= A2
– 6 A +9I










−
−
=∴










−
−
=










+










−
−−
−
−










−
−−
−
=⇒
−
−
311
131
113
4
1
311
131
113
100
010
001
9
211
121
112
6
655
565
556
4
1
1
A
A
39