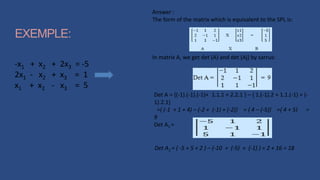
This document discusses two methods for solving systems of linear equations using matrix algebra: Cramer's Rule and the inverse matrix method. Cramer's Rule is described as a simple method that uses determinants and the inverse of the coefficient matrix to solve systems of linear equations. An example is shown working through applying Cramer's Rule to solve a 3x3 system. The inverse matrix method is also explained. It involves converting the system of equations to matrix form Ax=b, then solving the equivalent inverse form x=A^-1b to find the solution values. An example 2x2 system is worked through using the inverse matrix method. In summary, the document outlines Cramer's Rule and the inverse

1. APPLICATION OF
MATRIX ALGEBRA
IN ECONOMY
NAME : RAHMATUL FITRI
NIM : 21053101
COURSE : ECONOMIC EDUCATION

2. Solution of the Linear
Equation System
• Cramer's Method
Cramer's method is one of the simple and
practical methods in solving a system of
linear equations using the inverse matrix
equipment, namely Cramer's rule.
Cramer's rule is basically first using the
inverse matrix equipment, and then in the
next solution process the determinant
concept is used. This is reasonable,
because one way to obtain the inverse
value of a matrix requires its determinant
value. So, the determinant value will
determine whether a matrix has an
inverse value or not.

3. If a system of linear
equations is in matrix
form as follows:

4. Then the completion of the SPL with the
Cramer method, is calculated by the
following formula:

5. Where each matrix A1, A2, and A3 is searched
as follows:

6. EXEMPLE:
-x1 + x2 + 2x3 = -5
2x1 - x2 + x3 = 1
x1 + x2 - x3 = 5
Answer :
The form of the matrix which is equivalent to the SPL is:
In matrix A, we get det (A) and det (Aj) by sarrus:
Det A = {(-1).(-1).(-1)+ 1.1.1 + 2.2.1 } – { 1.(-1).2 + 1.1.(-1) + (-
1).2.1}
={ (-1 + 1 + 4) – (-2 + (-1) + (-2)} = { 4 – (-5)} ={ 4 + 5} =
9
Det A1 =
Det A1 = ( -5 + 5 + 2 ) – (-10 + (-5) + (-1) ) = 2 + 16 = 18

7. Det A2=
Det A2= (1 – 5 +20 ) – ( 2 + (-5) + 10 ) = 16 -7 = 9
Det A3=
Det A3= ( 5 + 1 + (-10) – ( 5 + (-1) + 10 ) = -4 -14 = -18
So we get:
X1= Det (A1 )/ Det (A) = 18 /9 = 2
X2 = Det (A2 )/ Det (A) = 9 / 9 = 1
X3 = Det (A3 )/ Det (A) = -18 / 9 = -2
So the solution for the SPL is:
X1= 2 , X2= 1 , X3= -2

8. • MATRIX INVERS METHOD
The purpose of solving a two-variable linear system
of equations is to determine the value of x and value
of y that satisfies the equation. Therefore, we must
convert the matrix form AX = B to inverse form as
follows.
AX = B
X = A-1B
A-1 is the inverse matrix A. Using the matrix inverse
formula above, the matrix form of X = A-1B is as
follows.
[
x
] =
1
[
d −b
] [
p
]
y ad – bc −c a q

9. EXEMPLE :
2x – 3y = 3
x + 2y = 5
First, we convert the above SPLDV into matrix
form AX = B
Second, we change the matrix AX = B to the
inverse form X = A-1B
Third, solve the matrix equation above
[
2 −3
] [
x
] =
[
3
]
1 2 y 5
So, we get the value of x = 3 and the value of y
= 1. Thus, the solution set for the above
system of linear equations is HP = {(3, 1)}.

10. THANK YOU 