Recommended
More Related Content
What's hot
What's hot (20)
Similar to 4. Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
Similar to 4. Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization (20)
Recently uploaded
Recently uploaded (20)
4. Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 1. Seminar Series on Linear Algebra for Machine Learning Part 4: Eigenvalues, Eigenvectors and Diagonalization Dr. Ceni Babaoglu Data Science Laboratory Ryerson University cenibabaoglu.com Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 2. Overview 1 Eigenvalues and eigenvectors 2 Some properties of eigenvalues and eigenvectors 3 Similar matrices 4 Diagonalizable matrices 5 Some properties of diagonalizable matrices 6 References Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 3. Eigenvalues and Eigenvectors When a matrix multiplies a vector in general the magnitude and direction of the vector will change. There are special vectors where only their magnitude is changed when multiplied by a matrix. These special vectors are called eigenvectors. The value by which the length changes is the associated eigenvalue. We say that x is an eigenvector of A if Ax = λx. λ is called the associated eigenvalue. Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 4. Eigenvalues and Eigenvectors The matrix A transforms 5 different vectors to other 5 different vectors. Vector (1) is transformed to vector (a), vector (2) is transformed to vector (b) and so on. Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 5. Eigenvalues and Eigenvectors All the vectors except vector (4) change both their magnitude and direction when transformed by A. Vector (4) changes only magnitude and does not change direction. Vector (4) is an eigenvector of A. λ = Magnitude of vector (d) Magnitude of vector (4) Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 6. Eigenvalues and Eigenvectors In this mapping the red arrow changes direction but the blue arrow does not. The blue arrow is an eigenvector of this mapping because it does not change direction, and since its length is unchanged, its eigenvalue is 1. Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 7. Some properties If λ1, λ2, · · · , λn are distinct eigenvalues of a matrix, then the corresponding eigenvectors e1, e2, · · · , en are linearly independent. If e1 is an eigenvector of a matrix with corresponding eigenvalue λ1, then any nonzero scalar multiple of e1 is also an eigenvector with eigenvalue λ1. A real, symmetric square matrix has real eigenvalues, with orthogonal eigenvectors (can be chosen to be orthonormal). Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 8. Some properties The equation Ax = λx can be written in the form (A − λI)x = 0 (1) λ is an eigenvalue of A if and only if (1) has a nontrivial solution. (1) has nontrivial solution if and only if A − λI is singular, or equivalently det(A − λI) = 0 → characteristic equation for A (2) If (2) is expanded, we obtain an nth degree polynomial in λ, p(λ) = det(A − λI) → characteristic polynomial Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 9. Similar Matrices A matrix B is said to be similar to a matrix A if there exists a nonsingular matrix S such that B = S−1 AS. For n × n matrices A and B, if A is similar to B, then the two matrices both have the same characteristic polynomial and, consequently, both have the same eigenvalues. Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 10. Diagonalizable Matrices An n × n matrix A is said to be diagonalizable if there exists a nonsingular matrix X and a diagonal matrix D such that X−1 AX = D. We say that X diagonalizes A. Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 11. Some Properties An n × n matrix A is diagonalizable if and only if A has n linearly independent eigenvectors. If A is diagonalizable, then the column vectors of the diagonalizing matrix X are eigenvectors of A and the diagonal elements of D are the corresponding eigenvalues of A. The diagonalizing matrix X is not unique. Reordering the columns of a given diagonalizing matrix X or multiplying them by nonzero scalars will produce a new diagonalizing matrix. Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 12. Some Properties If an n × n matrix A has n distinct eigenvalues, then A is diagonalizable. If the eigenvalues are not distinct, then A may or may not be diagonalizable, depending on whether A has n linearly independent eigenvectors. If A is diagonalizable, then A can be factored into a product XDX−1 . Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 13. Some Properties All the roots of the characteristic polynomial of a symmetric matrix are real numbers. If A is a symmetric matrix, then eigenvectors that belong to distinct eigenvalues of A are orthogonal. Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
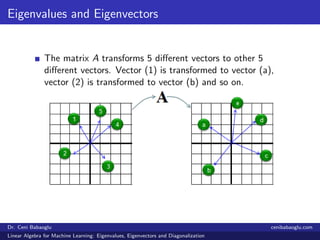
- 14. Example Diagonalize the matrix A = 2 −2 3 1 1 1 1 3 −1 We should solve the equation |A − λI| = 0. |A − λI| = 2 − λ −2 3 1 1 − λ 1 1 3 −1 − λ R2−R3→R2 −−−−−−−→ 2 − λ −2 3 0 −2 − λ 2 + λ 1 3 −1 − λ = (2 + λ) 2 − λ −2 3 0 −1 1 1 3 −1 − λ C2+C3→C2 −−−−−−−→ (2 + λ) 2 − λ 1 3 0 0 1 1 2 − λ −1 − λ = −(2 + λ) 2 − λ 1 1 2 − λ = −(2 + λ)[(2 − λ)2 − 1] = −(2 + λ)(λ2 − 4λ + 3) = 0. Eigenvalues: λ1 = 1, λ2 = 3, λ3 = −2. Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 15. Example A = 2 −2 3 1 1 1 1 3 −1 We solve the equation |A − λI| = 0. Eigenvalues: λ1 = 1, λ2 = 3, λ3 = −2. The 3 × 3 matrix A has 3 distinct real eigenvalues. It has 3 linearly independent eigenvectors which implies A is diagonalizable. Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 16. Example To find the eigenvector corresponding to λ1 = 1, we solve the homogeneous system (A − λ1I) u = 0. (A − I) u = 0 ⇒ 1 −2 3 1 0 1 1 3 −2 · u1 u2 u3 = 0 ⇒ 1 −2 3 1 0 1 1 3 −2 R2−R1→R2 R3−R1→R3 −−−−−−−→ 1 −2 3 0 2 −2 0 5 −5 R2/2→R2 R3/5→R3 −−−−−→ 1 −2 3 0 1 −1 0 1 −1 R1+2R2→R1 R3−R2→R3 −−−−−−−→ 1 0 1 0 1 −1 0 0 0 ⇒ u1 + u3 = 0 u2 − u3 = 0 ⇒ u1 = −u2 = −u3 = α An eigenvector corresponding to λ1 = 1 is −1 1 1 Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 17. Example To find the eigenvector corresponding to λ2 = 3, we solve the homogeneous system (A − λ2I) v = 0. ⇒ (A − 3I) v = 0 ⇒ −1 −2 3 1 −2 1 1 3 −4 · v1 v2 v3 = 0 ⇒ −1 −2 3 1 −2 1 1 3 −4 R2+R1→R2 R3+R1→R3 −−−−−−−→ −1 −2 3 0 −4 4 0 1 −1 −R1→R1 −R2/4→R2 −−−−−−−→ 1 2 −3 0 1 −1 0 1 −1 R1−2R2→R1 R3−R2→R3 −−−−−−−→ 1 0 −1 0 1 −1 0 0 0 ⇒ v1 − v3 = 0 v2 − v3 = 0 ⇒ v1 = v2 = v3 = α An eigenvector corresponding to λ2 = 3 is 1 1 1 Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 18. Example To find the eigenspace corresponding to λ3 = −2, we solve the homogeneous system (A − λ3I) w = 0. ⇒ (A + 2I) w = 0 ⇒ 4 −2 3 1 3 1 1 3 1 · w1 w2 w3 = 0 ⇒ 4 −2 3 1 3 1 1 3 1 R1−4R2→R1 R3−R2→R3 −−−−−−−→ 0 −14 −1 1 3 1 0 0 0 R1↔R2 −−−−→ 1 3 1 0 −14 −1 0 0 0 −R2/14→R2 −−−−−−−→ 1 3 1 0 1 1/14 0 0 0 R1−3R2→R1 −−−−−−−→ 1 0 11/14 0 1 1/14 0 0 0 ⇒ w1 + 11w3/14 = 0 w2 + w3/14 = 0 ⇒ w1 = 11α w2 = α w3 = −14α An eigenvector corresponding to λ3 = −2 is 11 1 −14 Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 19. Example X−1 AX = D −1/2 5/6 −1/3 1/2 1/10 2/5 0 1/15 −1/15 2 −2 3 1 1 1 1 3 −1 −1 1 11 1 1 1 1 1 −14 = 1 0 0 0 3 0 0 0 −2 A = XDX−1 2 −2 3 1 1 1 1 3 −1 = −1 1 11 1 1 1 1 1 −14 1 0 0 0 3 0 0 0 −2 −1/2 5/6 −1/3 1/2 1/10 2/5 0 1/15 −1/15 Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization
- 20. References Linear Algebra With Applications, 7th Edition by Steven J. Leon. Elementary Linear Algebra with Applications, 9th Edition by Bernard Kolman and David Hill. http://www.sharetechnote.com/html/Handbook_EngMath_Matrix_ Eigen.html https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors Dr. Ceni Babaoglu cenibabaoglu.com Linear Algebra for Machine Learning: Eigenvalues, Eigenvectors and Diagonalization