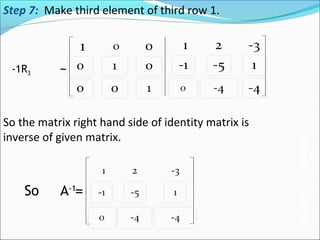
The document describes the Gauss-Jordan method for finding the inverse of a matrix. It involves 3 steps: 1) Writing the original matrix next to an identity matrix of the same size. 2) Performing row operations on both matrices to transform the original matrix into the identity matrix. 3) The resulting matrix next to the identity matrix is then the inverse of the original matrix. An example is shown applying the method to find the inverse of a 3x3 matrix through a series of row operations.

1. Inverse Of Matrix
By:=
Jitendra thakor

2. Gauss-Jordan Method for Inverses
Step 1: Write down the matrix A, and on its right write
an identity matrix of the same size.
Step 2: Perform elementary row operations on the
left-hand matrix so as to transform it into an
identity matrix. These same operations are
performed on the right-hand matrix.
Step 3: When the matrix on the left becomes an
identity matrix, the matrix on the right is the
desired inverse.
Main Procedure…
InverseOfMatrix

3. Example…
4 2 3
8 3 5 .
7 2 4
A
− 
 = − 
 − 
InverseOfMatrix

4. 4 2 3 1 0 0
8 3 5 0 1 0
7 2 4 0 0 1
 −
 
− 
 − 
4 2 3
8 3 5 .
7 2 4
A
− 
 = − 
 − 
Step 1: First take identity matrix of same size on it’s
right side.
~
InverseOfMatrix

5. Step 2: In this step we want to make first element of
first raw 1 and make 0 below this first element.
So take
R2-2R1 ~
C1 - C3 ~
InverseOfMatrix

6. Step 3: Then make second and third element of first
row 0 using column operation.
R2 – R1 &
R3 – 3R1
~
C2 + 2C1 &
C3 – C1
~
InverseOfMatrix

7. Step 4: Make second element of second row 1.
R2 – R3 ~
-1R2 ~
InverseOfMatrix

8. R3 – 4R2
~
R2 – R3
~
Step 5: Make 0 above and below of second element
of second row.
Step 6: Take column operation.
InverseOfMatrix

9. So A-1
=
-1R3 ~
Step 7: Make third element of third row 1.
So the matrix right hand side of identity matrix is
inverse of given matrix.
InverseOfMatrix

10. 10
Questions…???
InverseOfMatrix