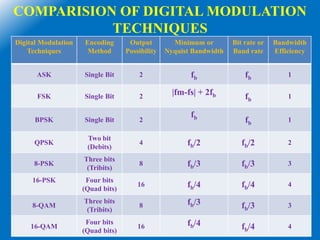
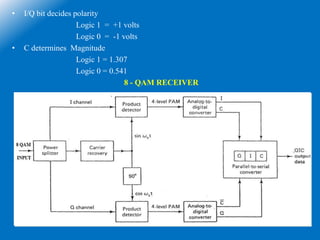
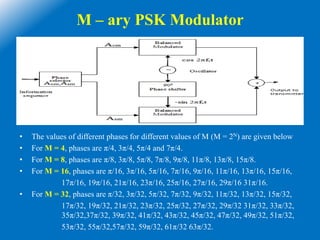
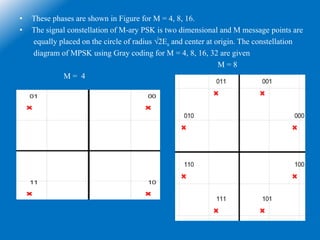
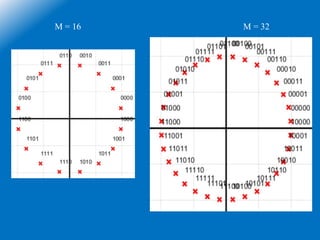
This document discusses M-ary digital modulation techniques. It begins by defining M-ary signaling as a technique where multiple bits are transmitted simultaneously using a single signal, instead of transmitting one bit at a time. It then provides the basic equation for calculating the number of possible conditions (M) based on the number of bits (N). The document goes on to describe several common M-ary modulation techniques including M-ary PSK, M-ary QAM, and their basic principles and equations. It provides examples of 4-PSK, 8-PSK, 16-PSK, 8-QAM and 16-QAM, explaining their modulation/demodulation, constellations, and minimum bandwidth requirements. Finally, it compares several

1. R.M.K. COLLEGE OF ENGINEERING AND TECHNOLOGY
DEPARTMENT OF CSE
EC 8395
COMMUNICATION ENGINEERING
Dr.Kannan K
Assistant Professor
Department of ECE

2. Phase shift keying – BPSK, DPSK, QPSK –
Principles of M- ary signaling M- ary PSK &
QAM – Comparison, ISI – Pulse shaping –
Duo binary encoding – Cosine filters – Eye
pattern, equalizers
UNIT III
DIGITAL MODULATION AND
TRANSMISSION

3. M – ary Signaling
An M - ary transmission is a type of digital modulation where instead of
transmitting one bit at a time, two or more bits are transmitted simultaneously
The word binary represents two-bits. M simply represents a digit that corresponds
to the number of conditions, levels, or combinations possible for a given number
of binary variables.
This is the type of digital modulation technique used for data transmission in
which instead of one-bit, two or more bits called symbol or symbols are
transmitted at a time.
As a single signal is used for multiple bit transmission, the channel bandwidth is
reduced.

4. M- ary Equation
If a digital signal is given under four conditions, such as voltage levels,
frequencies, phases and amplitude, then M = 4.
The number of bits necessary to produce a given number of conditions is
expressed mathematically as
N = Log2M
Where,
N is the number of bits necessary.
M is the number of conditions, levels, or
combinations possible with N bits.
The above equation can be re-arranged as 2N = M
For example, with two bits, 22 = 4 conditions are possible.(00,01,10 & 11)
In almost all applications, M = 2N and T = nTb, where n is an integer
Each of the M signals is called a symbol

5. Bit rate ,Baud rate and Minimum Bandwidth
With binary encoding, the bit rate and baud rate equal
b = fb
Here b – Baud rate(Symbol/Second)
fb – bit rate(bits/Second
With M – ary encoding, the relation between bit and baud rate is
b = fb/N
Here N – Number of bits encoded into each signaling element
According to Nyquist rate in the sampling therem,the minimum theoretical bandwidth
necessary to propagate a signal is called the minimum nyquist bandwidth or minimum
Nyquist frequency
fb = 2B
where fb – bit rate(bps)
B – Ideal Nyquist bandwidth
Using M –ary encoding, the Nyquist formula is fb = 2B log2M
Mlog
f
B
2
b

N
f
B b


6. In general, (M-ary) multi-level modulation techniques are used in
digital communications as the digital inputs with more than two modulation
levels allowed on the transmitter’s input. Hence, these techniques are bandwidth
efficient.
There are many different M-ary modulation techniques. Some of these
techniques, modulate one parameter of the carrier signal, such as amplitude,
phase, and frequency.
(i) M – ary ASK
(ii) M – ary PSK
(iii) M - ary FSK
(iv) M - ary QAM
Types of M- ary Techniques

7. M - ary PSK
• M-ary Phase Shift Keying is a very efficient signaling scheme
• The symbols are transmitted with different phase and frequency will remain
same.
• The number of possible signals are M = 2N, the duration of symbol is Ts =
NTb , where Tb is bit duration.
• In M - ary PSK, The PSK modulated signal can be written as

8. M- ary PSK Modulator
• The modulator structure is straight forward and is given . From the data, Acm & Asm are
obtained and fed into two balanced modulators.
• The output of both modulators are added to form a MPSK modulated signal. Substituting
value of phase in the above equation and expanding the cosine term, Sm (t) can be written
as

9. M – ary PSK Modulator
• The values of different phases for different values of M (M = 2N) are given below
• For M = 4, phases are π/4, 3π/4, 5π/4 and 7π/4.
• For M = 8, phases are π/8, 3π/8, 5π/8, 7π/8, 9π/8, 11π/8, 13π/8, 15π/8.
• For M = 16, phases are π/16, 3π/16, 5π/16, 7π/16, 9π/16, 11π/16, 13π/16, 15π/16,
17π/16, 19π/16, 21π/16, 23π/16, 25π/16, 27π/16, 29π/16 31π/16.
• For M = 32, phases are π/32, 3π/32, 5π/32, 7π/32, 9π/32, 11π/32, 13π/32, 15π/32,
17π/32, 19π/32, 21π/32, 23π/32, 25π/32, 27π/32, 29π/32 31π/32, 33π/32,
35π/32,37π/32, 39π/32, 41π/32, 43π/32, 45π/32, 47π/32, 49π/32, 51π/32,
53π/32, 55π/32,57π/32, 59π/32, 61π/32 63π/32.

10. • These phases are shown in Figure for M = 4, 8, 16.
• The signal constellation of M-ary PSK is two dimensional and M message points are
equally placed on the circle of radius √2Es and center at origin. The constellation
diagram of MPSK using Gray coding for M = 4, 8, 16, 32 are given
M = 8
M = 4

11. M = 16 M = 32

12. M - ary PSK Demodulator
 It is important in demodulation of the signal because the most likely errors caused by nois
e involve the erroneous selection of an adjacent phase to the transmitted signal phase. In
such a case, only a single bit error occurs in k-bit sequence.
 The general form of the optimum demodulator for detecting one of M signal in an AWGN
 channel is given.
 The low pass equivalent of transmitted signal is given by

13. The exponential factor under integral in the above equation is independent of the
variable of integration, hence it can be taken outside the integral.
The optimum demodulator can be implemented as a single matched filter or cross
correlator receiver which computes the decision variable Um and decides in favor of
maximum.

14. Equivalently the phase (θ) of the vector V is calculated by the phase detector
and optimum demodulator decides in favor of the signal having the phase closest
to the phase (θ).

15. 8 – PSK
M = 8, WKT 2N = 8 , N = 3
3 bits forming a group and produces 8 different output phases
I or Q determines the polarity of Signal logic 1 = +1 volts
logic 0 = -1 Volts
C or ̅C determines the Magnitude of the Signal
logic 1 = 1.307 volts
logic 0 = 0.541 volts
Bandwidth Efficiency
The bandwidth efficiency is defined as R/W where R is data rate and W is req
uired bandwidth

16. 8 – PSK TRANSMITTER

17. 8 - PSK Constellation Diagram and Truth Table

18. 8 – PSK Phasor Diagram

19. 8 – PSK Output Phase and Amplitude
Bandwidth
The Output of the Balanced Modulator
= (V Sinωat)(Sinωct)
Where V = ± 1.307 or ± 0.541
ωat = 2Πfat = 2Πfbt and ωct = 2Πfct
fa = Fundamental frequency = (fb/3)/2 = fb/6
= (V Sin 2Π(fb/6)t)(Sin2Πfct)
= V[1/2(Cos(fc-fb/6) - Cos(fc+fb/6))]
Here (fc + fb/6) – (fc - fb/6) = BW
Band Width = fb/6 + fb/6 = fb/3

20. 8 – PSK Receiver

21. 16 - PSK
• In this technique, M =16, i.e. 16 Different output phases
• M=2N ; 16 = 2N ; N = 4(4 bits)
• The minimum bandwidth and baud rate = 1/4th of bit rate i.e.. Fb/4
• With PSK, the angular separation between adjacent output phase is only 22.5o
• 16-PSK can undergo only a 11.25o phase shift during transmission and still
retain its integrity
• Truth Table Constellation Diagram

22. 16 – PSK Modulator and Demodulator

23. QAM
(QUADRATURE AMPLITUDE MODULATION
• QAM is a popular Scheme for high rate, high bandwidth efficiency systems
• QAM is a signal in which two carriers shifted in phase by 90 degrees (i.e. sine and
cosine) are modulated and combined. As a result of their 90° phase difference they
are in quadrature and this gives rise to the name. Often one signal is called the
In-phase or “I” signal, and the other is the quadrature or “Q” signal
• QAM = ASK + PSK
• M - ary Quadrature Amplitude Modulation or M - QAM is a modulation where
data bits select one of M combinations of amplitude and phase shifts that are applied
to the carrier
• The M possible waveforms may be described by M constellation points
• The term M as in M-QAM indicates how many bits are transmitted per time interval
or symbol for each unique amplitude/phase combination
• The simplest form of QAM is 2-QAM, more commonly called QPSK or quadrature
phase shift keying.

24. 8 - QAM
• In this M = 8,ie 8 output amplitudes and phases are possible
• M=2N ; 8 = 2N ; N = 3(Tribit).Three bits are grouped together
• Only difference is the removal of inverters in the C channel of 8 PSK transmitter
8 – QAM TRANSMITTER

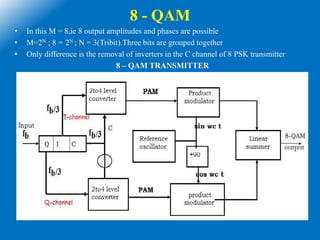
25. Output of balanced modulator can be expressed as
= Sinωat x Sinωct
=
where fa = (fb/3)/2 = fb/6
The output frequency spectrum range is from fc-fa to fc+fa
The minimum bandwidth or Nyquist bandwidth
B = (fc+fb/6)-(fc-fb/6)
B = fb/3
Bit rate at I or Q or C channel is = fb/3
The highest fundamental frequency fa = fb/2 (Generally)
= (fb/3)/2
= fb/6
]t)ff(2[Cos
2
1
]t)ff(2[Cos
2
1
acac 

26. 8 - QAM Truth Table

27. Phasor Diagram Constellation Diagram

28. 8 – QAM Output Phase and Amplitude

29. • I/Q bit decides polarity
Logic 1 = +1 volts
Logic 0 = -1 volts
• C determines Magnitude
Logic 1 = 1.307
Logic 0 = 0.541
8 - QAM RECEIVER

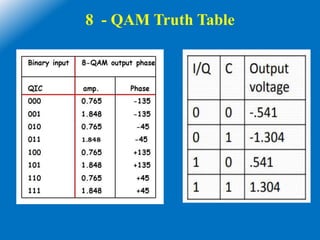
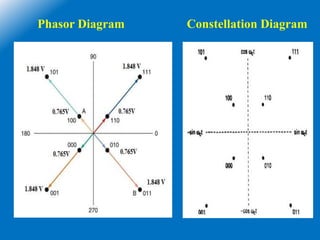
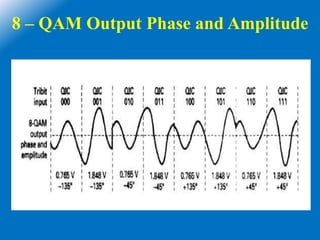
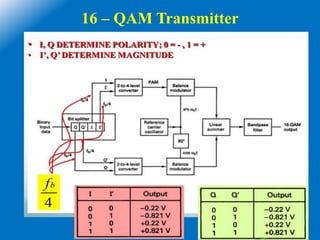
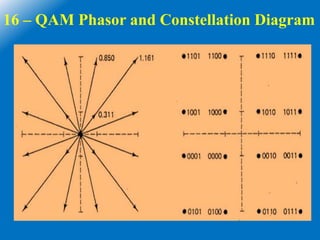
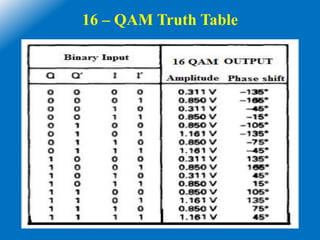
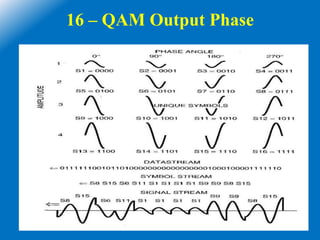
30. 16 - QAM
• Here M = 16, 16 = 2N,then N=4
• The minimum bandwidth and baud rate = one fourth of the bit rate = fb/4
• The fundamental frequency fa = fb/2 , but fb = fb/4
• fa = (fb/4)/2 = fb/8
• Output of the balanced modulator = Sinωat x Sinωct
=
Where fa = fb/8
• The output frequency spectrum ranges are (fc-fb/8) to (fc+fb/8)
• Minimum bandwidth or Nyquist bandwidth is
B = (fc+fb/8) – (fc-fb/8)
= fb/4
]t)ff(2[Cos
2
1
]t)ff(2[Cos
2
1
acac 

31. 16 – QAM Transmitter

32. 16 – QAM Phasor and Constellation Diagram

33. 16 – QAM Truth Table

34. 16 – QAM Output Phase

35. COMPARISION OF DIGITAL MODULATION
TECHNIQUES
Digital Modulation
Techniques
Encoding
Method
Output
Possibility
Minimum or
Nyquist Bandwidth
Bit rate or
Baud rate
Bandwidth
Efficiency
ASK Single Bit 2 fb fb 1
FSK Single Bit 2
|fm-fs| + 2fb fb 1
BPSK Single Bit 2
fb
fb 1
QPSK
Two bit
(Debits)
4 fb/2 fb/2 2
8-PSK
Three bits
(Tribits)
8 fb/3 fb/3 3
16-PSK Four bits
(Quad bits)
16 fb/4 fb/4 4
8-QAM
Three bits
(Tribits)
8 fb/3 fb/3 3
16-QAM
Four bits
(Quad bits)
16 fb/4 fb/4 4

36. Practical Applications
• BPSK:
WLAN IEEE802.11b (1 Mbps)
• QPSK:
WLAN IEEE802.11b (2 Mbps, 5.5 Mbps, 11 Mbps)
3G WDMA
DVB-T (with OFDM)
• QAM:
Telephone modem (16QAM)
Downstream of Cable modem (64QAM, 256QAM)
WLAN IEEE802.11a/g (16QAM for 24Mbps, 36Mbps; 64QAM for 38
Mbps and 54 Mbps)
LTE Cellular Systems
• FSK:
Cordless telephone
Paging system

37. THANK YOU