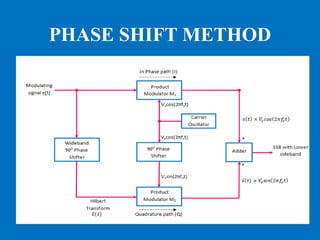
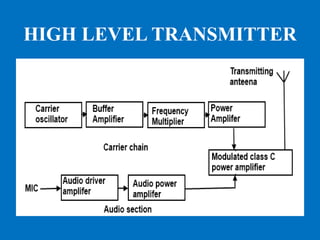
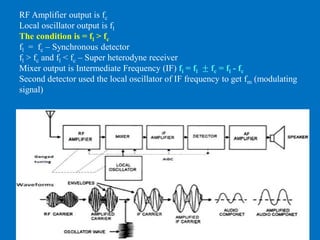
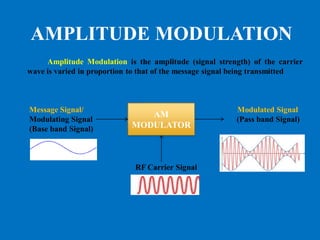
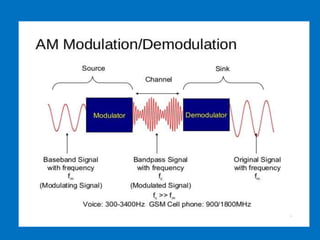
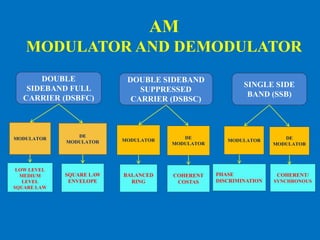
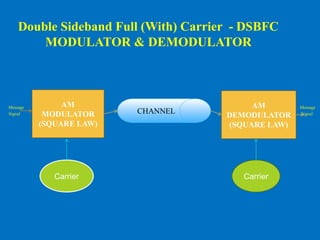
This document discusses various aspects of amplitude modulation (AM) including modulation, demodulation, and different types of AM modulators and demodulators. It describes how AM works by varying the amplitude of the carrier wave proportionally to the message signal. It also explains amplitude demodulation, the process of extracting the original message signal. Finally, it covers different AM systems like DSB-FC, DSB-SC, SSB and their corresponding modulators and demodulators like square law, balanced, and coherent detectors.

1. R.M.K. COLLEGE OF ENGINEERING AND TECHNOLOGY
DEPARTMENT OF CSE
EC 8395
COMMUNICATION ENGINEERING
Dr.Kannan Krishnan
Assistant Professor
Department of ECE

2. AMPLITUDE MODULATION
Amplitude Modulation is the amplitude (signal strength) of the carrier
wave is varied in proportion to that of the message signal being transmitted
Message Signal/ Modulated Signal
Modulating Signal (Pass band Signal)
(Base band Signal)
RF Carrier Signal
AM
MODULATOR

3. AMPLITUDE DEMODULATION
Amplitude Demodulation is the process by which the original information
bearing signal(message signal), i.e. the modulation is extracted from the incoming
overall received signal(modulated signal)
Modulated Signal Modulating Signal
(Pass band Signal) (Base band Signal)
RF Carrier Signal
AM
DEMODULATOR

5. AM
MODULATOR AND DEMODULATOR
DOUBLE
SIDEBAND FULL
CARRIER (DSBFC)
DOUBLE SIDEBAND
SUPPRESSED
CARRIER (DSBSC)
SINGLE SIDE
BAND (SSB)
MODULATOR
DE
MODULATOR MODULATOR DE
MODULATOR
MODULATOR DE
MODULATOR
LOW LEVEL
MEDIUM
LEVEL
SQUARE LAW
SQUARE LAW
ENVELOPE
BALANCED
RING
COHERENT
COSTAS
PHASE
DISCRIMINATION
COHERENT/
SYNCHRONOUS

6. Double Sideband Full (With) Carrier - DSBFC
MODULATOR & DEMODULATOR
Message Message
Signal Signal
AM
MODULATOR
(SQUARE LAW)
CHANNEL
AM
DEMODULATOR
(SQUARE LAW)
Carrier Carrier

7. DSBFC (Double Sideband Full (With) Carrier)
SQUARE LAW MODULATOR
In electronic signal processing, a square law detector is a device that produces
an output proportional to the square of some input.
A square law detector provides an output directly proportional to the power of
the input electrical signal.
In a square law modulator band pass filters are used to generate the AM signal.

8. DSBFC (Double Sideband Full Carrier)
SQUARE LAW MODULATOR
V1(t) = m(t) + Ac Cos(2πfct) (1)
V2(t) = k1V1(t) + k2V1
2(t) (2)
Where k1 & k2 are constants
Sub V1(t) in equation 2,

10. SQUARE LAW - DEMODULATOR
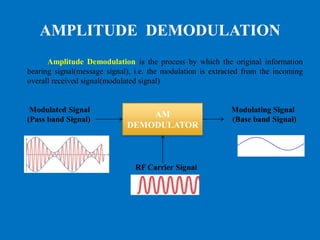
The process of extracting an original message signal from the modulated
wave is known as detection or demodulation. The circuit, which demodulates the
modulated wave is known as the demodulator
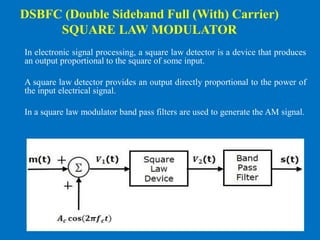
The Standard form of AM wave is
V1(t) = Ac[1+kam(t)]Cos(2πfct)
V2(t) = k1V1(t)+k2V1
2(t) (1)
Where, V1(t) is the input of the square law device, which is nothing but the
AM wave
V2(t) is the output of the square law device
k1 and k2 are constants

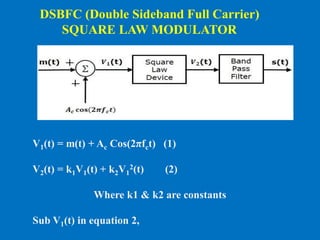
12. BALANCED MODULATOR
Balanced Modulator consists of two identical AM modulators.
These two modulators are arranged in a balanced configuration in
order to suppress the carrier signal. Hence, it is called as Balanced
modulator.
Double Side Band Suppressed
Carrier (DSBSC) - MODULATOR
The same carrier signal
C(t) = Ac Cos (2πfct) is applied as one of
the inputs to these two AM modulators.
Output of the upper AM modulator is
S1(t) = Ac[1+kam(t)]Cos(2πfct)
Output of the lower AM modulator is
S2(t) = Ac[1−kam(t)]Cos(2πfct)

13. s1(t) with positive sign and s2(t) with negative sign are applied as inputs to
summer block.
Thus, the summer block produces an output s(t) which is the difference of s1(t)
and s2(t).
s(t) = Ac[1+kam(t)]cos(2πfct) − Ac [1−kam(t)]cos(2πfct)
s(t) = Accos(2πfct)+ Ac kam(t)cos(2πfct)− Ac cos(2πfct)+ Ac kam(t)cos(2πfct)
s(t) = 2 Ac ka m(t)cos(2πfct)
We know the standard equation of DSBSC wave is
S(t)= Ac m(t)cos(2πfct)
By comparing the output of summer block with the standard equation of
DSBSC wave, we will get the scaling factor as 2ka

14. The process of extracting an original message signal from DSBSC wave is known
as detection or demodulation of DSBSC.
COHERENT DETECTOR
In Coherent detection the same carrier signal (which is used for generating
DSBSC signal) is used to detect the message signal. Hence, this process of detection is
called as coherent or synchronous detection. Following is the block diagram of the
coherent detector.
DSBSC - DEMODULATOR

15. Let the DSBSC wave be s(t) = Ac Cos(2πfct) m(t)
The output of the local oscillator is c(t) = Ac Cos(2πfct+ϕ)
From the figure, Output of product modulator as v(t) = s(t) c(t)
v(t) = Ac Cos(2πfct) m(t) Ac Cos(2πfct + ϕ)
= Ac2 Cos(2πfct) Cos (2πfct + ϕ) m(t)
= Ac2 /2[Cos(4πfct + ϕ) + Cosϕ ]m(t)
v(t) = Ac2 /2 Cosϕm(t) + Ac2/2Cos (4πfct + ϕ)m(t)
Here the first term is the scaled version of the message signal. It can be extracted by
passing the above signal through a low pass filter.
Therefore, the output of low pass filter is V0t = Ac2 /2Cosϕm(t)
 The demodulated signal amplitude will be maximum, when ϕ = 00
 That’s why the local oscillator signal and the carrier signal should be in phase, i.e.,
there should not be any phase difference between these two signals.

16. PHASE DISCRIMINATOR
A discriminator circuit selects the minimum pulse height. When the input
pulse exceeds the discriminator preset level, the discriminator generates an output
pulse
Single Side Band (SSB)
MODULATOR

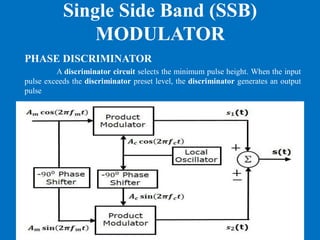
17. The modulating signal = Am cos (2πfmt)
The carrier signal = Ac cos (2πfct)
The output of upper product modulator is
S1(t) = Am cos (2πfmt) Ac cos (2πfct)
= Am Ac /2{cos[2π(fc+fm)t]+cos[2π(fc−fm)t]}
The output of lower product modulator is
S2(t) = Am Ac cos(2πfmt −900)cos(2πfct −900)
= Am Ac sin(2πfmt)sin(2πfct)
= Am Ac/ 2{cos[2π(fc−fm)t] − cos[2𝜋(fc+fm)t]}
At the Summer S(t) = S1(t) + S2(t)

18. S(t) = Am Ac /2{cos[2π(fc+fm)t]+cos[2π(fc−fm)t]} +
Am Ac/ 2{cos[2π(fc−fm)t] − cos[2𝜋(fc+fm)t]}
S(t) = Am Ac cos2π(fc−fm)t
Subtract S2(t) from S1(t) to get S(t)
S(t) = Am Ac /2{cos[2π(fc+fm)t]+cos[2π(fc−fm)t]} -
Am Ac/ 2{cos[2π(fc−fm)t] − cos[2𝜋(fc+fm)t]}
S(t) = Am Ac cos2π(fc+fm)t
Hence, by properly choosing the polarities of inputs at
summer block, we will get SSBSC wave having a upper
sideband or a lower sideband.

19. The process of extracting an original message signal from
SSBSC wave is known as detection or demodulation of SSBSC.
Coherent detector is used for demodulating SSBSC wave.
SSB DEMODULATOR

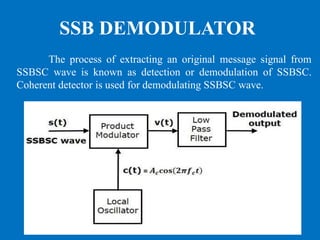
20. Consider the following SSBSC wave having a LOWER SIDEBAND
S(t) = Am Ac / 2 Cos[2π(fc−fm)t]
The output of the local oscillator is
C(t) = Ac Cos(2πfct)
From the figure, we can write the output of product modulator as v(t) = s(t)c(t)
v(t) = Am Ac /2 Cos[2π(fc−fm)t] AcCos(2πfct)
= Am Ac
2 /2 Cos[2π(fc−fm)t] Cos(2πfct)
= Am Ac
2 /4{Cos2π(2fc−fm)t + Cos(2πfm)t}
In the above equation, the Second term is the scaled version of the message
signal. It can be extracted by passing the above signal through a low pass filter.
The output of low pass filter is
V0(t)=Am Ac
2 /4 Cos(2πfmt)
Here, the scaling factor is Ac2/4

21. Methods of SSB Generation
- Filter Method
- Phase shift Method
- Weaver’s Method or Third Method
SSB GENERATION

22. PHASE SHIFT METHOD

23. The message signal x(t) is applied to the product modulator M1 and through a 90o
phase shifter to the product modulator M2 .
Hence, we get the Hilbert transform at the output of the wideband 90o phase
shifter .
The output of carrier oscillator is applied as it is to modulator M1 whereas it s
passed through a 90o phase shifter and applied to the modulator M2 .
The outputs of M1 and M2 are applied to an adder .
Therefore,
This expression represents the SSB signal with only LSB i.e. it rejects the USB .

24. AM
TRANSMITTER AND
RECEIVER
Transmitter
(i) Low level transmitter
(ii) High level transmitter
Receiver
(i) Tuned Radio Frequency receiver
(ii) Super heterodyne receiver

25. HIGH LEVEL TRANSMITTER

26. The requirements of AM receiver is
 It should be cost-effective.
 It should receive the corresponding modulated waves.
 The receiver should be able to tune and amplify the desired
station.
 It should have an ability to reject the unwanted stations.
 Demodulation has to be done to all the station signals,
irrespective of the carrier signal frequency.
For these requirements to be fulfilled, the tuner circuit and the
mixer circuit should be very effective.
The procedure of RF mixing is an interesting phenomenon.
AM RECEIVER

27. The AM super heterodyne receiver takes the amplitude modulated wave as
an input and produces the original audio signal as an output.
Selectivity is the ability of selecting a particular signal, while rejecting the
others.
Sensitivity is the capacity of detecting RF signal and demodulating it, while
at the lowest power level. – Large Gain
Fidelity is its ability to accurately reproduce, in its output, the signal that
appears at its input.
To achieve better selectivity, sensitivity and fidelity super heterodyne
receiver is used.
SUPER HETERODYNE
RECEIVER

28. RF Amplifier output is fc
Local oscillator output is fl
The condition is = fl > fc
fl = fc – Synchronous detector
fl > fc and fl < fc – Super heterodyne receiver
Mixer output is Intermediate Frequency (IF) fi = fl ± fc = fl - fc
Second detector used the local oscillator of IF frequency to get fm (modulating
signal)

29. IF Amplifier
- High Selectivity and High sensitivity is implemented
- High gain is achieved
AM Radio
- 540 KHz to 1600 KHz
- IF Frequency = 455 KHZ
Image frequency fsi = fc + 2fi - Two stations are tuned to same
frequency
The image frequency rejection is done by tuned circuits in the RF
stage i.e before IF stages
Advantages
- Better selectivity
- Simple IF amplifier design

30. In a super heterodyne receiver the input AM Signal has a center
frequency of 1425kHz and bandwidth 10khz.The input is down
converted to 455khz.What is the image frequency?
Solution
Given : fs = 1425 ± 5khz ; Since bandwidth of AM signal = 10khz
fi = 455khz
The image frequency is
fsi = fs + 2fi
= 1425 ± 5khz + 2 x 455 kHz
= 2335 ± 5khz
= 2330 to 2340 kHz
Thus image frequency can be any value that lies in the range of 2330
kHz to 2340 kHz
PROBLEM

32. THANK YOU