The document proposes a method called SUMO (Stochastically Unbiased Marginalization Objective) for estimating log marginal probabilities in latent variable models. SUMO uses a Russian roulette estimator to obtain an unbiased estimate of the log marginal likelihood. This allows SUMO to provide an objective function for variational inference that converges to the log marginal likelihood as more samples are taken, avoiding the bias issues of methods like VAEs and IWAE. The paper outlines SUMO, compares it to existing methods, and demonstrates its effectiveness on density estimation tasks.

1. 1
SUMO: Unbiased Estimation of Log Marginal Probability
for Latent Variable Models
Shohei Taniguchi, Matsuo Lab

2. ॻࢽ৘ใ
SUMO: Unbiased Estimation of Log Marginal Probability for Latent Variable Models
Yucen Luo, Alex Beatson, Mohammad Norouzi, Jun Zhu, David Duvenaud, Ryan P.
Adams, Ricky T. Q. Chen
https://arxiv.org/abs/2004.00353
ICLR 2020 accepted
(஫) Θ͔Γ΍͢͞ͷͨΊʹɺൃදͰ͸࿦จதͱ‫ه‬๏͕ҟͳΔ෦෼͕͋Γ·͢

3. ֓ཁ
જࡏม਺Ϟσϧͷର਺पล໬౓ͷෆภਪఆ
• VAEͳͲͷજࡏม਺Ϟσϧͷֶश͸ҎԼͷର਺पล໬౓ͷ࠷େԽͰߦΘΕΔ
• ର਺पล໬౓͸௨ৗ‫͍ͳ͖Ͱࢉܭ‬ͷͰɺVAEͰ͸୅ΘΓʹͦͷԼքΛ࠷େԽ
• ຊ࿦จͰ͸ɺԼքͰ͸ͳ͘ର਺पล໬౓Λ௚઀࠷େԽ͢Δํ๏ΛఏҊ
• Russian roulette estimatorΛ࢖͏ςΫχοΫ͕໘ന͍
log pθ (x) = log
∫
pθ (x, z) dz

4. Outline
1. ෆภਪఆྔ
2. જࡏม਺Ϟσϧ (VAE, IWAE)
3. Stochastically Unbiased Marginalization Objective (SUMO)
• Russian roulette estimator
• ෼ࢄ௿‫ݮ‬
• ࣮‫ݧ‬

5. ෆภਪఆྔ

6. ෆภਪఆྔ
Unbiased Estimator
ਪఆ͍ͨ͠ྔɿ ɹਪఆྔɿ
͕੒Γཱͭͱ͖ʮ ͸ ͷෆภਪఆྔͰ͋Δʯͱ͍͏
y ̂
y
𝔼
[ ̂
y] = y ̂
y y

7. ෆภਪఆྔ
Unbiased Estimator
Ex. 1: ਖ਼‫ن‬෼෍ͷ฼ฏ‫ۉ‬ͷਪఆ
σʔλ ͕ਖ਼‫ن‬෼෍ ͔ΒಘΒΕͨͱ͢Δ
αϯϓϧฏ‫ۉ‬ ͸฼ฏ‫ۉ‬ ͷෆภਪఆྔ
x(1)
, …, x(n)
𝒩
(x; μ, σ2
)
x̄ =
∑
n
i=1
x(i)
n
μ
𝔼
[x̄] =
𝔼
[
∑
n
i=1
x(i)
n ]
=
1
n
n
∑
i=1
𝔼
[x(i)
] = μ

8. ෆภਪఆྔ
Unbiased Estimator
Ex. 2: ϛχόονֶश
‫ݧܦ‬ଛࣦ
ϛχόον౷‫ྔܭ‬ ͸ ͷෆภਪఆྔ
͸ ͔ΒҰ༷ϥϯμϜʹબ͹Εͨ΋ͷ
Ln =
1
n
n
∑
i=1
l (x(i)
, θ)
̂
Lm =
1
m
m
∑
i=1
l (x̃(i)
, θ) Ln
x̃ x(1)
, …, x(n)

9. ෆภਪఆྔ
Unbiased Estimator
Ex. 3: Reparameterization trick
Λਪఆ͍ͨ͠
ͱͯ͠ ͸ ͷෆภਪఆྔ
• VAEͷΤϯίʔμͷޯ഑ਪఆʹ࢖ΘΕΔ
∇θ
𝔼
pθ(x) [f (x)] (pθ (x) =
𝒩
(x; μθ, σθ))
ϵ ∼
𝒩
(ϵ; 0,1) ∇θ f (μθ + ϵ ⋅ σθ) ∇θ
𝔼
pθ(x) [f (x)]
𝔼
ϵ∼
𝒩
(ϵ; 0,1) [∇θ f (μθ + ϵ ⋅ σθ)] = ∇θ
𝔼
pθ(x) [f (x)]

10. ෆภਪఆྔ
Unbiased Estimator
Ex. 4: Likelihood ratio gradient estimator (REINFORCE)
Λਪఆ͍ͨ͠
ͱͯ͠ ͸ ͷෆภਪఆྔ
• ‫ڧ‬Խֶशͷํࡦޯ഑๏Ͱ࢖ΘΕΔ
∇θ
𝔼
pθ(x) [f (x)]
x ∼ pθ (x) f (x)∇θlog pθ (x) ∇θ
𝔼
pθ(x) [f (x)]
𝔼
pθ(x) [f (x)∇θlog pθ (x)] = ∇θ
𝔼
pθ(x) [f (x)]

11. ෆภਪఆྔ
ͳͥෆภੑ͕ॏཁ͔
• ‫ػ‬ցֶशͰ͸ɺ‫ݧܦ‬ଛࣦ͕࠷খʹͳΔύϥϝʔλΛޯ഑๏౳Ͱ୳͢
• ‫ݧܦ‬ଛࣦ͕‫͍ͳ͖Ͱࢉܭ‬৔߹Ͱ΋ɺ‫ݧܦ‬ଛࣦͷෆภਪఆྔ͕‫͖Ͱࢉܭ‬Ε͹
‫ॴہ‬ղ΁ͷऩଋ͕อূͰ͖Δ৔߹͕ଟ͍
e.g., ֬཰తޯ഑߱Լ๏ (stochastic gradient descent, SGD)
ϛχόονਪఆྔΛ༻͍ͨޯ഑๏͸ɺద੾ʹֶश཰Λεέδϡʔϧ͢Ε͹
‫ॴہ‬ղ΁ͷऩଋ͕อূ͞Ε͍ͯΔ

12. ༗ޮਪఆྔ
Efficient Estimator
ਪఆྔ͕ෆภੑΛ΋͍ͬͯͯ΋ɺ෼ࢄ͕େ͖͍ͱ҆ఆͨ͠ਪఆ͕Ͱ͖ͳ͍
Ex. 1: SGDͰόοναΠζ͕খ͍͞ͱ෼ࢄ͕େ͖͘ͳΓֶश͕҆ఆ͠ͳ͍
Ex. 2: Reparameterization trick͸Ұൠʹlikelihood ratio estimatorΑΓ௿෼ࢄ
ཧ૝తͳਪఆྔ͸ ෆภਪఆྔ͔ͭ෼ࢄ͕খ͍͞΋ͷ
ෆภਪఆྔͷதͰ෼ࢄ͕࠷খͱͳΔ΋ͷΛಛʹ༗ޮਪఆྔͱ͍͏

13. જࡏม਺Ϟσϧ

14. જࡏม਺Ϟσϧ
Latent Variable Models
ੜ੒ϞσϧͰΑ͘࢖ΘΕΔϞσϧ
ύϥϝʔλ ͷֶश͸ɺର਺पล໬౓ͷ࠷େԽͰߦ͏
pθ (x) =
∫
pθ (x, z) dz
θ
log pθ (x) = log
∫
pθ (x, z) dz

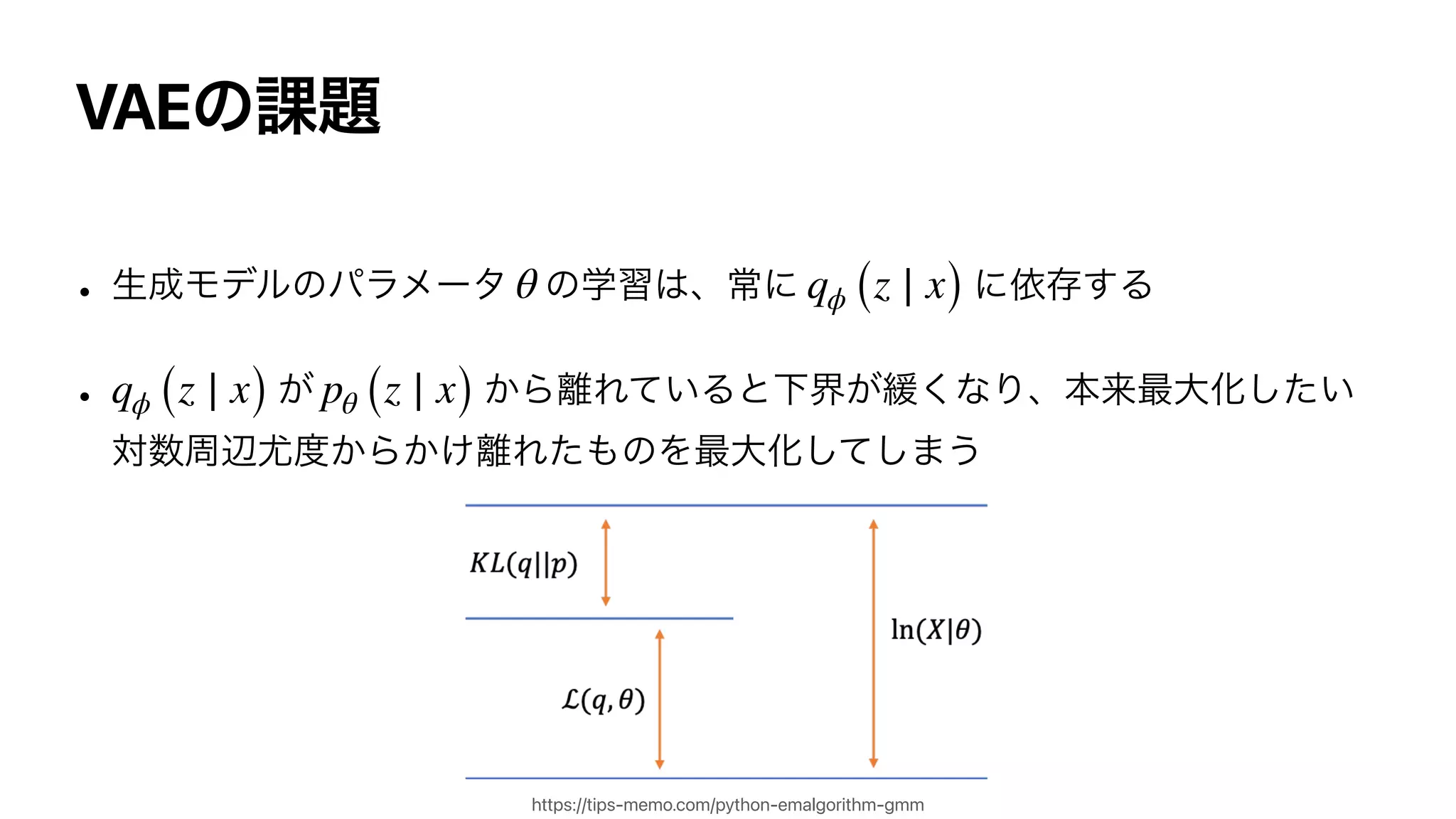
15. ม෼ਪ࿦
Variational Inference
ର਺पล໬౓͸௚઀‫͍ͳ͖Ͱࢉܭ‬ͷͰɺม෼ԼքΛ༻͍Δ
͜ͷෆ౳ࣜ͸ ͷͱ͖౳߸੒ཱ
➡ Λ ʹͳΔ΂͍ۙ͘෼෍͔Βબ΂͹ྑ͍
log pθ (x) = log
∫
pθ (x, z) dz
≥
𝔼
q(z) [
log
pθ (x, z)
q (z) ]
= ℒ (θ, q)
q (z) = pθ (z ∣ x)
q (z) pθ (z ∣ x)

16. ม෼ࣗ‫߸ූݾ‬Խ‫ث‬
Variational Autoencoder,VAE
ʹ΋ύϥϝʔλΛ΋ͨͤͯ ͱͯ͠ಉ࣌ʹֶश͢Δ
໨తؔ਺͸ ͱͷKL divergenceͷ࠷খԽ
ୈ1߲͸ ʹґଘ͠ͳ͍ͷͰɺ݁‫ہ‬ ͱ ͸ͱ΋ʹ ͷ࠷େԽͰֶशͰ͖Δ
ͷޯ഑ͷਪఆʹ͸ɺઌड़ͷreparameterization trickΛ࢖͏
q (z) qϕ (z ∣ x)
pθ (z ∣ x)
KL (qϕ (z ∣ x) ∥ pθ (z ∣ x)) = log pθ (x) − ℒ (θ, qϕ)
ϕ θ ϕ ℒ
ϕ

17. VAEͷ՝୊
• ੜ੒Ϟσϧͷύϥϝʔλ ͷֶश͸ɺৗʹ ʹґଘ͢Δ
• ͕ ͔Β཭Ε͍ͯΔͱԼք͕؇͘ͳΓɺຊདྷ࠷େԽ͍ͨ͠
ର਺पล໬౓͔Β͔͚཭Εͨ΋ͷΛ࠷େԽͯ͠͠·͏
θ qϕ (z ∣ x)
qϕ (z ∣ x) pθ (z ∣ x)
https://tips-memo.com/python-emalgorithm-gmm

18. VAEͷվળ
1. ͷද‫ྗݱ‬Λ্͛Δ
• ʹ͸ਖ਼‫ن‬෼෍Λ࢖͏͜ͱ͕ଟ͍͕ɺΑΓॊೈͳ෼෍Λ࢖͏͜ͱͰ
Լք͕λΠτʹͳΔΑ͏ʹ͢Δ
• Normalizing flow, implicit variational inference
2. ໨తؔ਺Λมߋ͢Δ
• Լք͕λΠτʹͳΔΑ͏ͳ໨తؔ਺Λ࢖͏
qϕ
qϕ

19. VAEͷվળ
1. ͷද‫ྗݱ‬Λ্͛Δ
• ʹ͸ਖ਼‫ن‬෼෍Λ࢖͏͜ͱ͕ଟ͍͕ɺΑΓॊೈͳ෼෍Λ࢖͏͜ͱͰ
Լք͕λΠτʹͳΔΑ͏ʹ͢Δ
• Normalizing flow, implicit variational inference
2. ໨తؔ਺Λมߋ͢Δ
• Լք͕λΠτʹͳΔΑ͏ͳ໨తؔ਺Λ࢖͏
qϕ
qϕ

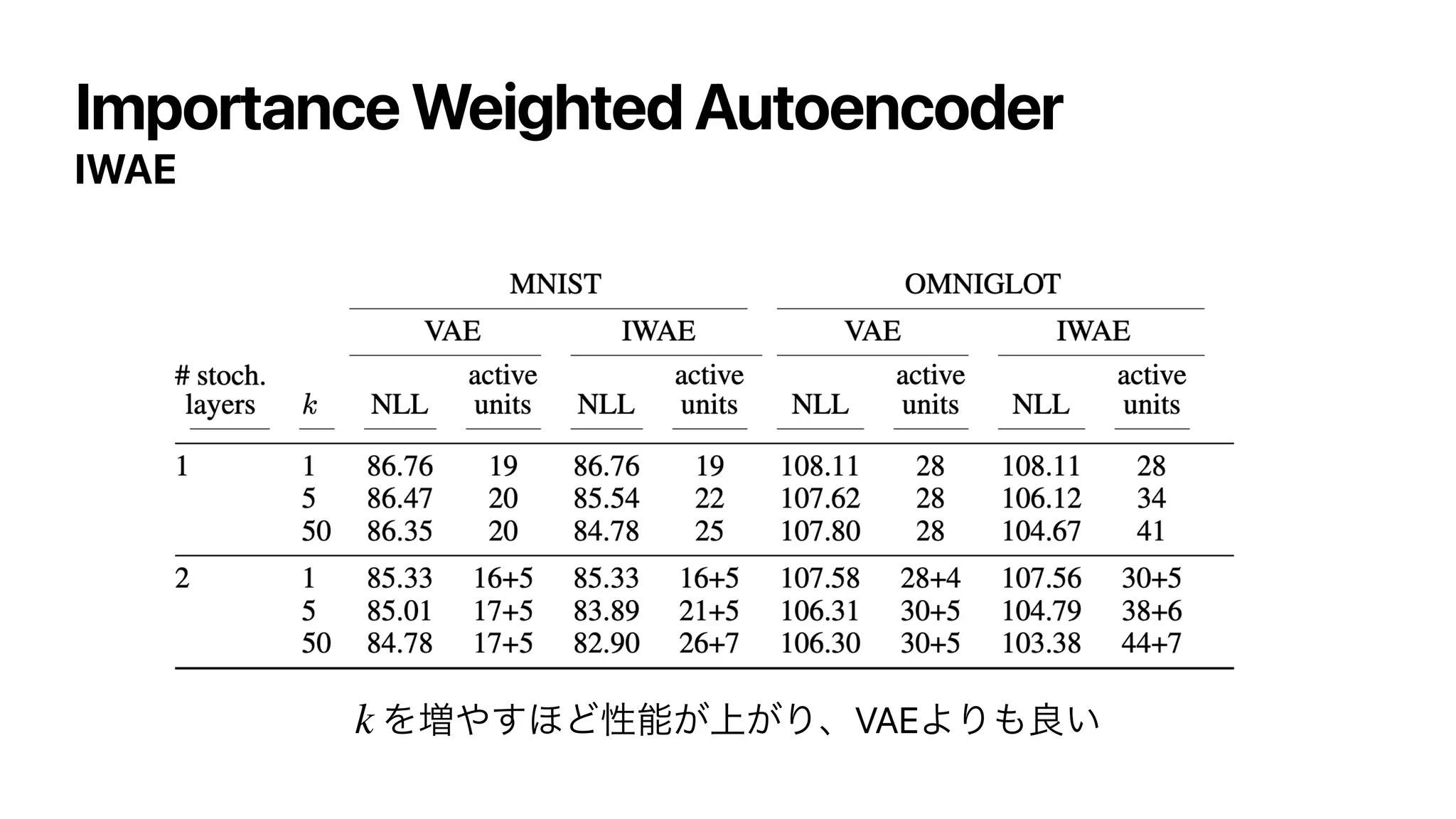
20. Importance Weighted Autoencoder
IWAE
• ͷͱ͖ɺVAEͷม෼ԼքͱҰக
• Ͱ౳߸੒ཱ
log pθ (x) = log
𝔼
z(1),…,z(k)∼q(z)
[
1
k
k
∑
i=1
pθ (x, z(i)
)
q (z(i)
) ]
≥
𝔼
z(1),…,z(k)∼q(z)
[
log
1
k
k
∑
i=1
pθ (x, z(i)
)
q (z(i)
) ]
= ℒk (θ, q)
k = 1
k → ∞

21. Importance Weighted Autoencoder
IWAE
Λ૿΍͢΄Ͳੑೳ্͕͕ΓɺVAEΑΓ΋ྑ͍
k

22. Stochastically Unbiased
Marginalization Objective

23. SUMO
Stochastically Unbiased Marginalization Objective
• IWAEͰ΋ɺ Λे෼૿΍͞ͳ͍ͱԼք͸λΠτʹͳΒͳ͍
• ԼքͰ͸ͳ͘ɺ౳߸͕ৗʹ੒ΓཱͭྔʢʹෆภਪఆྔʣͰֶश͍ͨ͠
• ෆภਪఆྔΛಘΔํ๏͸ͳ͍͔ʁ
➡ Russian roulette estimatorΛ࢖͏
k

24. Russian Roulette Estimator
ͱ͓͘ͱɺ‫਺ڃ‬ ͸ର਺पล໬౓ͱҰக͢Δ
Δk =
{
ℒ1 (θ, q) (k = 1)
ℒk (θ, q) − ℒk−1 (θ, q) (k ≥ 2)
∞
∑
k=1
Δk
∞
∑
k=1
Δk = ℒ∞ (θ, q) = log pθ (x)

25. Russian Roulette Estimator
ҎԼͷΑ͏ͳ Λߟ͑Δ
1. ֬཰ Ͱද͕ग़ΔίΠϯΛৼΔ
2. ද͕ग़ͨΒ Ҏ߱Λ‫͠ࢉܭ‬ɺ Ͱׂͬͨ΋ͷΛ ʹ଍͢
ཪ͕ग़ͨΒ ͚ͩΛ‫͢ࢉܭ‬Δ
̂
y
̂
y = Δ1 +
∑
∞
k=2
Δk
μ
⋅ b, b ∼ Bernoulli (μ)
μ
k = 2 μ Δ1
Δ1

26. Russian Roulette Estimator
͸ ͷෆภਪఆྔͰ͋Δ͜ͱ͕Θ͔Δ
̂
y
∞
∑
k=1
Δk
̂
y = Δ1 +
∑
∞
k=2
Δk
μ
⋅ b, b ∼ Bernoulli (b; μ)
𝔼
[ ̂
y] = Δ1 +
∑
∞
k=2
Δk
μ
⋅
𝔼
[b] =
∞
∑
k=1
Δk

27. Russian Roulette Estimator
ಉ͜͡ͱΛ Ҏ߱΋‫܁‬Γฦ͢ͱɺҎԼͷ ΋ ͷෆภਪఆྔʹͳΔ
͸࠷ॳʹཪ͕ग़Δ·ͰʹίΠϯΛৼͬͨճ਺ʢ‫ز‬Կ෼෍ʹै͏ʣ
͜ͷ Λ࢖͑͹ɺର਺पล໬౓ͷෆภਪఆྔ͕ಘΒΕΔ
k = 2 ̂
y
∞
∑
k=1
Δk
̂
y =
K
∑
k=1
Δk
μk−1
, K ∼ Geometric (K; 1 − μ)
K
̂
y

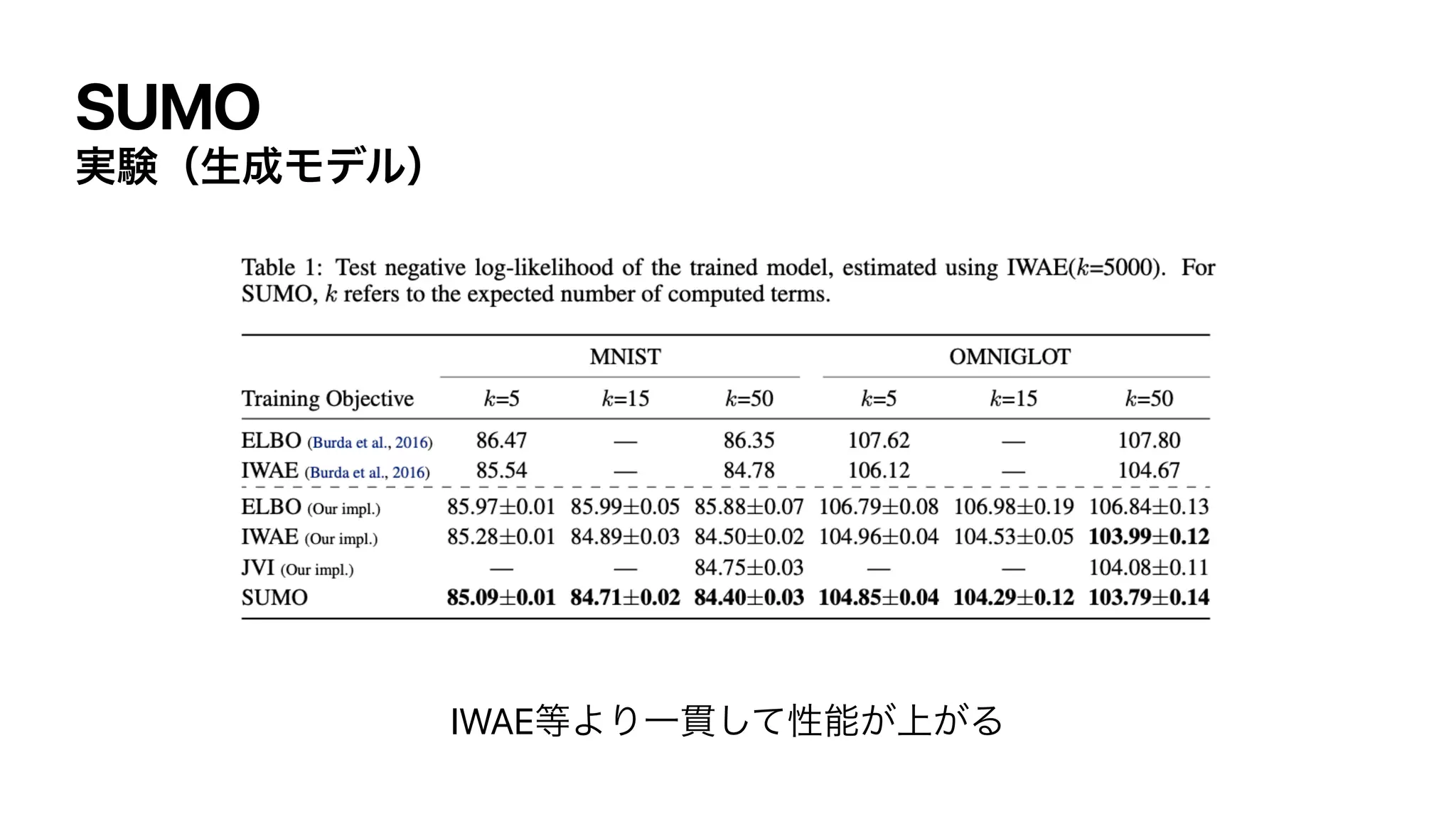
28. SUMO
Stochastically Unbiased Marginalization Objective
log pθ (x) =
𝔼
K∼p(K)
[
K
∑
k=1
Δk
μk−1 ]
= ℒ1 (θ, qϕ) +
𝔼
K∼p(K)
K
∑
k=2
ℒk (θ, qϕ) − ℒk−1 (θ, qϕ)
μk−1
VAEͱಉ͡
ิਖ਼߲

29. SUMO
Stochastically Unbiased Marginalization Objective
SUMO͸ର਺पล໬౓ͷෆภਪఆྔ
SUMO (x) = log w(1)
+
K
∑
k=2
log
1
k
∑
k
i=1
w(i)
− log
1
k − 1
∑
k−1
i=1
w(i)
μk−1
w(i)
=
pθ (x, z(i)
)
qϕ (z(i) ∣ x)
, K ∼ p (K), z(1)
, …, z(K)
∼ qϕ (z ∣ x)
𝔼
K∼p(K), z(1),…,z(K)∼qϕ(z ∣ x) [SUMO (x)] = log pθ (x)

30. SUMO
෼ࢄ௿‫ݮ‬
SUMO͸ ͷબͼํʹΑͬͯɺ෼ࢄͱ‫ྔࢉܭ‬ͷτϨʔυΦϑ͕ੜ·ΕΔ
• খ͍͞ ͕ग़΍͍͢෼෍Λબ΂͹ɺ‫ྔࢉܭ‬͸‫ݮ‬ΒͤΔ͕෼ࢄ͸େ͖͘ͳΔ
࠷ॳͷ ճ෼͸ඞͣ Λ‫͢ࢉܭ‬ΔΑ͏ʹ͢Δ͜ͱͰ΋ɺ෼ࢄΛ௿‫͖Ͱݮ‬Δ
p (K)
K
m Δk
SUMOm (x) = log
1
m
m
∑
i=1
w(1)
+
m+K−1
∑
k=m+1
log 1
k
∑
k
i=1
w(i)
− log 1
k − 1
∑
k−1
i=1
w(i)
μk−1

31. SUMO
Τϯίʔμͷֶश
SUMO͸ɺΤϯίʔμଆ͔Β‫ͨݟ‬Βύϥϝʔλ ʹؔͯ͠ఆ਺
VAEͷΑ͏ʹɺಉ͡ϩεͰֶशͯ͠΋ҙຯ͕ͳ͍
࿦จͰ͸ɺਪఆྔͷ෼ࢄΛ࠷খԽ͢ΔΑ͏ʹֶश͢Δ͜ͱΛఏҊ͍ͯ͠Δ
ϕ
∇ϕ
𝕍
[SUMO (x)] =
𝔼
[∇ϕ(SUMO (x))2
]

32. SUMO
࣮‫ݧ‬ʢੜ੒Ϟσϧʣ
IWAE౳ΑΓҰ؏ͯ͠ੑೳ্͕͕Δ

33. SUMO
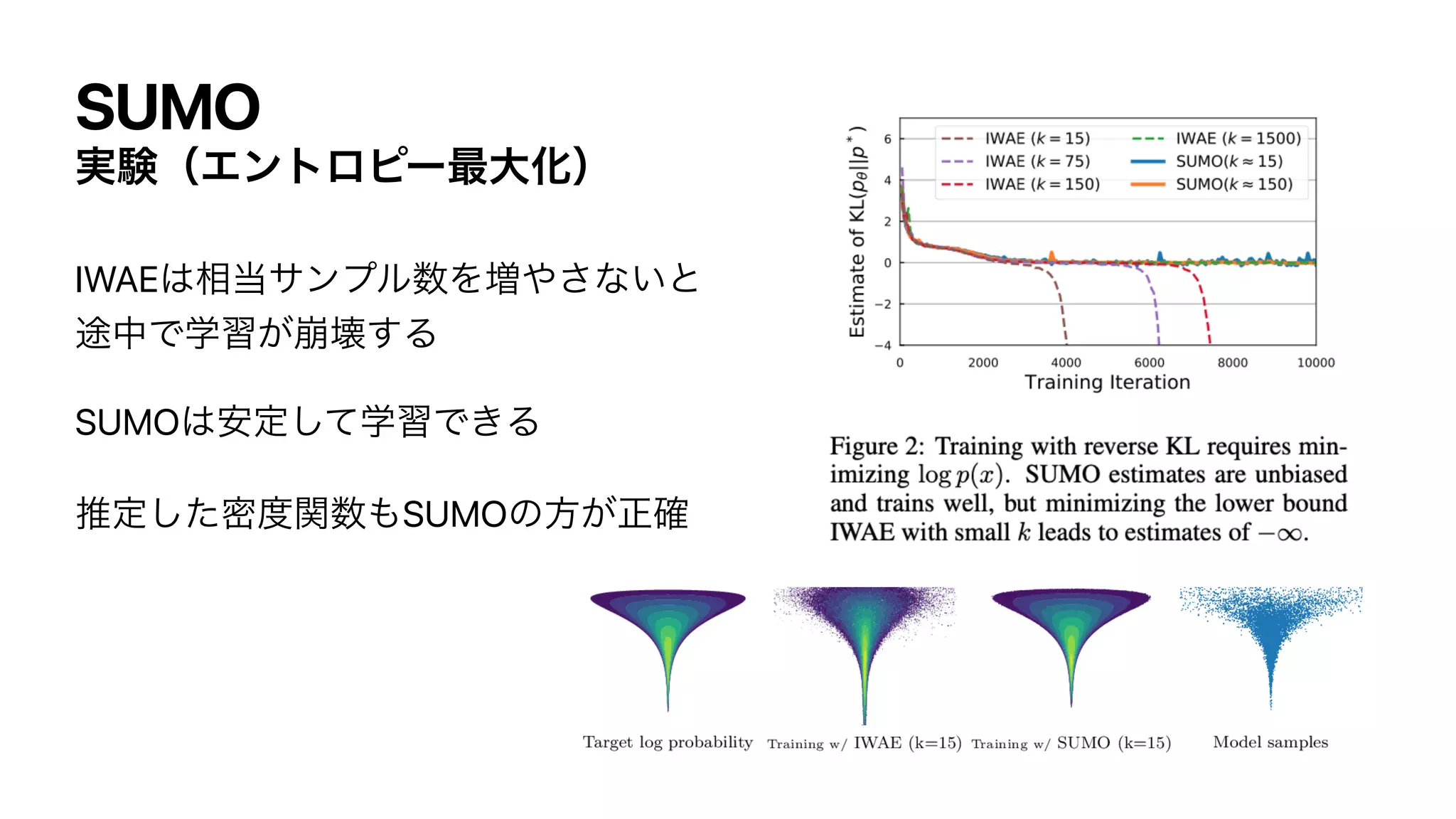
Τϯτϩϐʔ࠷େԽ
ີ౓ؔ਺͸Θ͔͍ͬͯΔ͕ɺαϯϓϦϯά͕೉͍͠෼෍ Λۙࣅ͍ͨ͠
͜ΕΛજࡏม਺ϞσϧͰֶश͢Δͱ͖ɺreverse KLͷ࠷খԽ͕Α͘࢖ΘΕΔ
ୈ1߲ͷΤϯτϩϐʔ߲ͷ‫͕ࢉܭ‬೉͍͠
p* (x)
min
θ
KL (pθ(x)∥ p*(x)) = min
θ
𝔼
x∼pθ(x) [log pθ(x) − log p*(x)]

34. SUMO
Τϯτϩϐʔ࠷େԽ
ͷਪఆʹIWAEΛ࢖͏ͱɺ໨తؔ਺ͷԼքΛ࠷খԽͯ͠͠·͏
SUMOΛ࢖͑͹ɺ͜ͷ໰୊ΛճආͰ͖Δɹ
log pθ (x)
𝔼
pθ(x) [log pθ (x)] ≥
𝔼
pθ(x),z(1),…,z(k)∼qϕ(z ∣ x)
[
log
1
k
k
∑
i=1
pθ (x, z(i)
)
q (z(i)
) ]
=
𝔼
pθ(x) [log pθ (x) − KL (q̃θ,ϕ (z ∣ x) ∥ pθ (z ∣ x))]
𝔼
pθ(x) [log pθ (x)] =
𝔼
[SUMO (x)]
͜͜Λ࠷େԽ͠Α͏ͱͯ͠͠·͏

35. ࣮‫ݧ‬ʢΤϯτϩϐʔ࠷େԽʣ
IWAE͸૬౰αϯϓϧ਺Λ૿΍͞ͳ͍ͱ
్தͰֶश่͕յ͢Δ
SUMO͸҆ఆֶͯ͠शͰ͖Δ
ਪఆͨ͠ີ౓ؔ਺΋SUMOͷํ͕ਖ਼֬
SUMO

36. SUMO
REINFORCE΁ͷԠ༻
REINFORCEͰ͸ɺ ͕‫͖Ͱࢉܭ‬Δඞཁ͕͋Δ
ʹજࡏม਺ϞσϧΛ࢖͏ͱɺ؆୯ʹ‫ͳ͘ͳ͖Ͱࢉܭ‬Δ
e.g., ‫ڧ‬Խֶशͷํࡦʹજࡏม਺ϞσϧΛ࢖͏
log pθ (x)
∇θ
𝔼
pθ(x) [f (x)] =
𝔼
pθ(x) [f (x)∇θlog pθ (x)]
pθ (x)
πθ (a ∣ s) =
∫
pθ (z) pθ (a ∣ s, z) dz

37. SUMO
REINFORCE΁ͷԠ༻
SUMOΛ࢖͑͹ɺ͜Ε΋ෆภਪఆͰ͖Δ
∇θ
𝔼
pθ(x) [f (x)] =
𝔼
pθ(x) [f (x)∇θlog pθ (x)]
=
𝔼
[f (x)∇θSUMO (x)]

38. SUMO
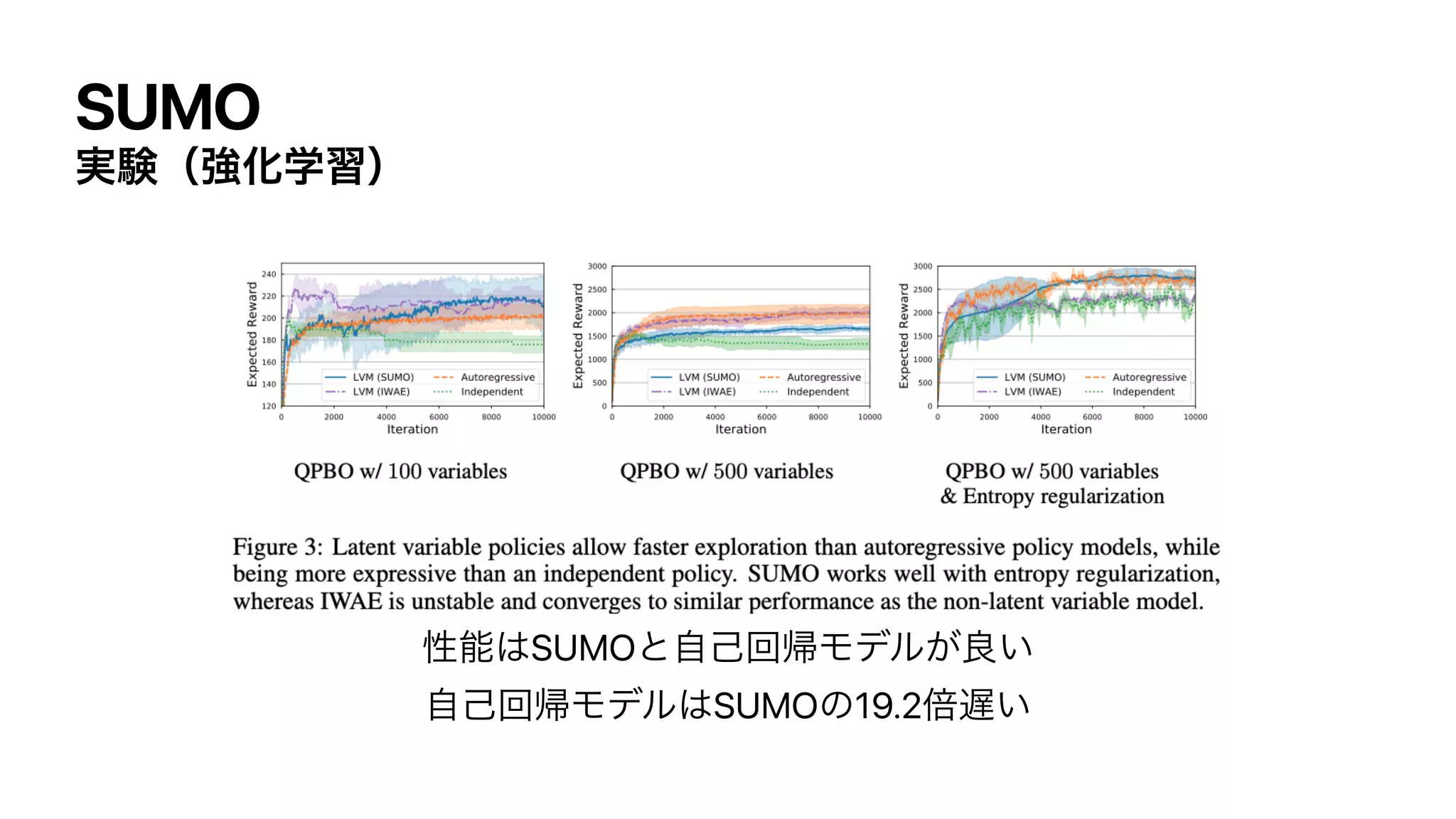
࣮‫ݧ‬ʢ‫ڧ‬Խֶशʣ
࣌‫ྻܥ‬Λ‫͍ͳ·ؚ‬؆୯ͳ‫ڧ‬Խֶशͷ໰୊Ͱɺ ͷ࠷େԽΛߟ͑Δ
ֶश͸REINFORCEΛ࢖ͬͯɺํࡦޯ഑๏Ͱߦ͏
ํࡦ ʹજࡏม਺ϞσϧΛ࢖͏৔߹ʹ͸ɺSUMO͕࢖͑Δ
𝔼
x∼pθ(x)[R(x)]
∇θ
𝔼
x∼pθ(x)[R(x)] =
𝔼
pθ(x) [R (x)∇θlog pθ (x)]
pθ (x)
∇θ
𝔼
x∼pθ(x)[R(x)] =
𝔼
[R (x)∇θSUMO (x)]

39. SUMO
࣮‫ݧ‬ʢ‫ڧ‬Խֶशʣ
ํࡦ ͱͯ͠
1. જࡏม਺Ϟσϧ
2. ࣗ‫ݾ‬ճ‫ؼ‬Ϟσϧ
3. ಠཱϞσϧ
ͷ3ͭΛൺ΂ɺ1. ͷֶशʹIWAEͱSUMOΛ༻͍Δ৔߹΋ൺֱ͢Δ
pθ (x)

40. SUMO
࣮‫ݧ‬ʢ‫ڧ‬Խֶशʣ
1. જࡏม਺Ϟσϧɿ
ද‫͘ߴ͕ྗݱ‬ɺαϯϓϦϯά΋଎͍
2. ࣗ‫ݾ‬ճ‫ؼ‬Ϟσϧɿ
ද‫ྗݱ‬͸ߴ͍͕ɺαϯϓϦϯά͕஗͍
3. ಠཱϞσϧɿ
ද‫ྗݱ‬͸௿͍͕ɺαϯϓϦϯά͕଎͍
pLVM(x) :=
∫ ∏
pθ (xi ∣ z) p(z)dz
pAutoreg (x) :=
∏
p (xi ∣ x<i)
pIndep (x) :=
∏
p (xi)

41. SUMO
࣮‫ݧ‬ʢ‫ڧ‬Խֶशʣ
ੑೳ͸SUMOͱࣗ‫ݾ‬ճ‫ؼ‬Ϟσϧ͕ྑ͍
ࣗ‫ݾ‬ճ‫ؼ‬Ϟσϧ͸SUMOͷ19.2ഒ஗͍

42. ·ͱΊ
• જࡏม਺Ϟσϧͷֶशʹ͸ɺର਺पล໬౓ͷԼքͷ࠷େԽ͕࢖ΘΕ͖ͯͨ
• ຊ‫Ͱڀݚ‬͸ɺRussian roulette estimatorΛ༻͍ͯର਺पล໬౓ͷෆภਪఆྔΛ
௚઀࠷େԽ͢Δख๏SUMOΛఏҊ
• SUMO͸ɺreverse KL࠷খԽ΍ɺ‫ڧ‬ԽֶशͳͲʹ΋Ԡ༻Ͱ͖Δ
‫ײ‬૝
• ൚༻ੑͷ͋ΔΞΠσΞͰɺ৭Μͳͱ͜ΖͰ࢖͑ͦ͏ʢ૬‫ޓ‬৘ใྔ‫͔ͱܥ‬ʣ