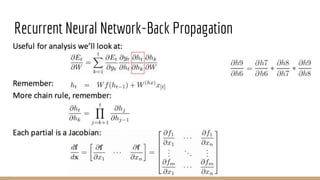
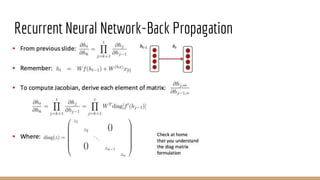
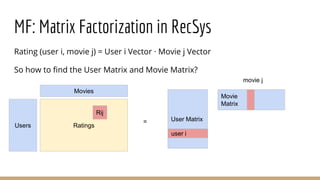
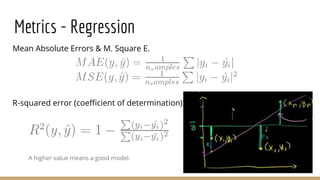
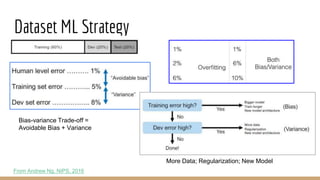
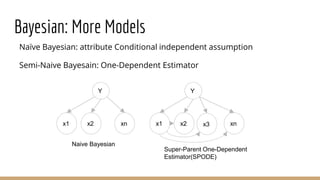
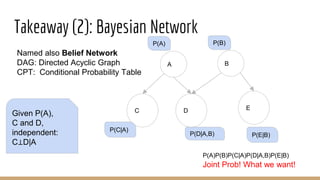
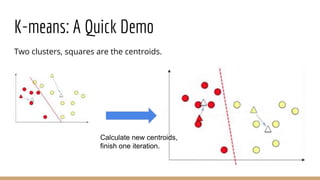
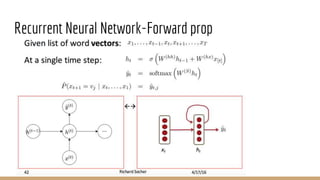
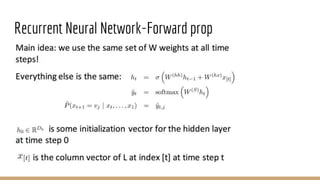
This document provides an overview of machine learning algorithms and techniques. It discusses classification and regression metrics, naive Bayesian classifiers, clustering methods like k-means, ensemble learning techniques like bagging and boosting, the expectation maximization algorithm, restricted Boltzmann machines, neural networks including convolutional and recurrent neural networks, and word embedding techniques like Word2Vec, GloVe, and matrix factorization. Key algorithms and their applications are summarized at a high level.

1. ML Algorithms
Part 2 Draft
Do you really understand more...

2. Outline
Learning Theory: Model, Evaluation Metrics
Algorithems: Naïve Bayesian, Clustering Methods (K-means)
Ensemble Learning, EM Algorithm
Restricted Boltzman Machines
Neural Networks: BP, Word2Vec, GloVe, CNN, RNN
Other: Singular Vector Decompostion, Matrix Factorization

3. Discriminative & Generative Model
Decision Function Y=f(X) or conditional probability P(Y|X)
Generative Model: learn P(X,Y), calculate posterior prob dist P(Y|X):
HMM, Bayesian Classifier
Discriminative Model: learn P(Y|X) directly
DT, NN,SVM,Boosting,CRF

4. Metrics - Classification
Accuracy
Precision & Recall (generally binary classification)
TP(Pos->Pos) FP(Neg->Pos)
FN(Pos->Neg) TN(Neg->Neg)
F1 score
P & R are high, F1 is high.

5. Metrics - Regression
Mean Absolute Errors & M. Square E.
R-squared error (coefficient of determination):
A higher value means a good model.

6. Dataset ML Strategy
From Andrew Ng, NIPS, 2016
Bias-variance Trade-off =
Avoidable Bias + Variance
More Data; Regularization; New Model

7. Naive Bayesian Classifier
Two Assumptions
Bayes’ Theorem
Features are conditionally independent
How to do?
Learn Joint probability distribution p(x,y)
Learn p(x)
Calculate p(y)

8. Naïve Bayesian: Notations
Dataset:
Priori probability: K classes
Conditional probability:
Then learn Joint: P(X,Y) = P(Y) P(X|Y) = P(X)P(Y|X)
Calculate Posterior: P(Y|X)

9. Naïve Bayesian: Attribute Conditional independent assumption
Each input x is a vector with n elements.
Given the class y, features are conditionally
independent.
Y
x1 x2

10. Naïve Bayesian: Calculation
https://en.wikipedia.org/wiki/Bayes'_theorem

11. Naïve Bayesian: Calculation
So we can rewrite this part:

12. Naïve Bayesian: Definition
Want the class that has the max of the probabilities:
For everyone, the denominators are the same, so we can simplify it:

13. Naïve Bayesian: Parameter Estimation
Maximum Likelihood Estimation
Goal: estimate priori P(Y=c) for each class
estimate P(X=x | Y=c) for each class
Count(x,y)
--------------- = P(x|y)
Count(y)

14. Naïve Bayesian: Cost
Choose 0-1 cost function:
Right answer = 0
Wrong answer = 1
-- L gives “how big” it is making the mistake...we want to minimize it!
Add up those we go wrong
1- Right cases
Minimize the errors ⇔ Maximize the right

15. Naïve Bayesian: Calculation
Calculate a prob with an input x:
Decide the class of the input x:
A demo from the book.

16. Naïve Bayesian: Bayesian Estimation
When do MLE, could be 0 counts. Then you times it...all become 0.
Add one more thing, lambda >= 0. If lambda = 0, it is MLE; If lambda = 1, it is
Laplace smoothing.
Laplace smoothing, it is a probalistic distribution.
Priori Prob’s Bayesian Estimation:

17. Bayesian: More Models
Naïve Bayesian: attribute Conditional independent assumption
Semi-Naive Bayesain: One-Dependent Estimator
Y
x1 x2 xn
Naive Bayesian
Y
x1 x2 xn
Super-Parent One-Dependent
Estimator(SPODE)
x3

18. Takeaway (1): Probabilistic Graphical Models
Y
x1 x2 xn
Naive Bayesian
P(Y)
P(xn|Y)
P(y)P(x1|y)P(x2|y)..P(xn|y)
Joint Prob! What we want!
P(x1|Y)
Find out More: https://www.coursera.org/learn/probabilistic-graphical-models （Prof.Daphne Koller）

19. Takeaway (2): Bayesian Network
A
C D E
P(A)P(B)P(C|A)P(D|A,B)P(E|B)
Joint Prob! What we want!
Named also Belief Network
DAG: Directed Acyclic Graph
CPT: Conditional Probability Table
B
P(A) P(B)
P(C|A)
P(E|B)P(D|A,B)
Given P(A),
C and D,
independent:
C⊥D|A

20. Clustering: Unsupervised Learning
Similarty Methods: Eculidean Distance, etc.
In-group: high similarity
Out-group: high distance
Methods
Prototype-based Clustering: K-means, LVQ, MoG
Density-based Clustering: DBSCAN
Hierarchical Clustering: AGNES,DIANA

21. Prototype-based Clustering: k-means
Dataset D, Clusters C
Error(each one in each cluster)

22. K-means: Algorithm
(Input: whole dataset points x1,...xm)
Initialization: Randomly place centroids c1..ck
Repeat until convergence (stop when no points changing):
- for each data point xi:
find nearest centroid, set the point to the centroid cluster
- for each cluster:
calculate new centroid (means of all new points)
https://www.youtube.com/watch?v=_aWzGGNrcic
argmin D (xi,cj) for all cj
O(#iter * #clusters * #instances *
#dimensions)

23. K-means: A Quick Demo
Two clusters, squares are the centroids.
Calculate new centroids,
finish one iteration.

24. K-means
k-modes:
-cat,frequency
k-prototype:
- num+cat
From Uiversity College Dublin, Prof. Tahar.

25. Clustering: Other Methods(1)
Prototype-based Clustering
LVQ: Find out a group of vectors to describe the clusters, with labels
MoG: describe the model by a probabilistic model.
Density-based Clustering
DBSCAN

26. Clustering: Other Methods(2)
Hierarchical Clustering : AGNES,DIANA

27. Ensemble Learning
Strong learning method: learns model with good performance;
Week learning method: learns model slightly better than random.
Ensemble learning methods:
Iterative method: Boosting
Parallel method: Bagging

28. Boosting: Algorithm
Boosting: gather/ensemble week learners to become a strong one.
Through majority voting on classification; average on regression.
Algo:
1) Feed N data to train a week learner/ model: h1.
2) Feed N data to train another one: h2; N pieces of data including: h1 errors and new
data never trained before.
3) Repeat to train hn, N includes previous errors and new data.
4) Get final model: h_final=Majority Vote(h1,h2,..,hn)

29. Bagging: Bootstrap AGGregatING
Bootstrap sampling: take k/n with replacement at each time. Samples are
overlapped. Appro. 36.8% would not be selected. If we sample m times:
Training: in parallelization.
Ensemble: voting on classification; average on regression.
Random Forest: a variant of Bagging.

30. Random Forest: Random Attribute Selection
Bagging: select a number of data to train each DT.
Random Attribute Selection
Each tree, each node, select k attributes, then find out the optimum.
Emperical k:
where d is the total number of attributes.

31. Expectation Maximization: Motivation
Expectation Maximization:
- An iterative method to maximum the likelihood function.
- Always used for estimate parameters in statistical models.
Example:
Three coins: A, B and C. For each throw step, first throw coin A. If positive,
throw B, otherwise, throw C. Repeat those steps n times independently.
The face up probability of A, B and C is 𝝅, 𝘱 and 𝘲.
If we only can observe the results not the process, how can we get the
face up probability of those coins?

32. Expectation Maximization
Suppose we are in step i, we have once observed results y (1 or 0). we did not
know next throw results z. 𝛳 = ( 𝝅, 𝘱, 𝘲) the parameters of the model. Then the
whole probability of next throw will be:
according to Bayesian:

33. Expectation Maximization
Extend to whole steps, if overall observed results follows
Non-observed values refer as
The face up probability among whole steps will be:
Now, using EM algorithm to estimate the parameters.

34. Expectation Maximization: Expectation(1)
Expectation function using initial parameters:
Parameters in step i, refer as:
The expectation function is step i:

35. Expectation Maximization: Expectation(2)
Calculate
then,
the next goal is to maximum function Q.

36. Expectation Maximization: Maximization
In order to compute the maximum of function Q. We calculate its derivative
value of each parameter.

37. Expectation Maximization
Convergence condition: ϵ1 and ϵ2 is a quit small positive value
or

38. Restricted Boltzmann Machine
Basic concepts:
h: status vector of hidden units (0/1)
v: status vector of visible units (0/1)
b: bias vector of hiddens units
a: bias vector of visible units
W: weight vector between each
hidden units and visible units

39. Fundamental theory of RBM:
energe between visible units v and hidden units h:
probability distribution through energy function:
z is the partition function in physic, which is not important part in RBM
Restricted Boltzmann Machine

40. Suppose activate probability of hidden units
Visible units
Input(x) ⇒ v:
- calculate activate probability of every hidden units by v, p(h1, v1)
- using gibbs sampling selecting a sample to represents whole hidden layer: h1 ~ p(h1, v1)
- calculate activate probability of every visible units by h1, p(v2, h1)
- using gibbs sampling selecting a sample to represents whole visible layer: v2 ~ p(v2, h1)
- calculate activate probability of every hidden units by v2, p(h2, v2)
- then update:
RBM: Contrastive Divergence (train)

41. Deductive active probability (take hidden units as example)
- For a hidden unit k:
- then, introduce two equation below:
- It is obviously to see:
- where, it represents the energy parts of j quals to k and not equals to k

42. Deductive active probability
According to contrastive divergence, when calculate a hidden units, visible units already know.
Meanwhile, other hidden units also should be known.
- First, using Bayes function
- Because other hidden units status in 0 or 1:
- cooperate with the probability distribution function

43. Deductive active probability
(previous step):
- with transformed energy function:
- With same theory, we get the active probability of visible units:

44. Back Propagation: Main Purpose
The main purpose of back propagation is to find the partial derivatives ∂C/∂
w means all parameters in the network including weights and biases.
Cost function:
where n is the sample number and a(x) is the output of the network
Note:
It is useful to first point out the naive forward propagation algorithm implied by the
chain rule. Then we can find out the advantages of back propagation by simply
comparing 2 algorithms.

45. Naive Forward Propagation
Naive forward propagation algorithm using chain rule to compute the partial
derivatives on every node of the network in a forward manner.
How it works:
1.Compute ∂ui/∂uj for every pair of nodes where ui
is at a higher level than uj.
2.In order to compute , , we need to compute
for every input of ,. Thus the total work
in the algorithm is O(VE).
( v = node number, e = edge number)

46. Back Propagation -Calculate Error
If we try to change the value of
(z is the input of the node), it will affect the
result of the next layer and finally affect the
output.
Assume is close to 0, then change the
value of z will not help us to minimize the cost C, in this case we can say that
node is close to optimum.
Naturally we can define error as:

47. Back Propagation -Calculate Error
Using chain rule, we can deduce
By replacing the parital derivative with vector:
∇aC is a vector with elements equal to ∂C/∂aLj
⊙ is hadamard operater

48. Back Propagation -Back Propagation
From layer l+1 to layer l, trying to use to represent
(1)
where
(2)
By combine (1) and (2):

49. Back Propagation -From error to parameters
After calculating the error, we finally need one more step:
Using error to calculate the derivatives on parameters(weights and biases)
Given the equation:
For bias b:
For weight w:

50. Convolutional Neural Network -Convolution Layer

51. Convolutional Neural Network -Pooling Layer
The main idea of “Max Pooling Layer” is to capture the most important activation
(maximum overtime):
e.g.
Q: This operation shrinks the feature number(from n-h+1 to 1), how can we get more features?
A: Applying multiple filters with different window sizes and different weights.

52. Convolutional Neural Network -Multi-channel
Start with 2 copies of the word vectors, then pre-train one of them(word2vec
or Glove), this action change the value of vectors of it. Keep the other one
static.
Apply the same filter on them, then sum the Ci of them before max pooling

53. Convolutional Neural Network -Dropout
Create a masking vector r with random variables 0 or 1. To delete some of the
features to prevent co-adaption(overfitting)
Kim (2014) reports 2 – 4% improved accuracy and ability to use very large networks without overfitting

54. Word Vectors- Taxonomy
Idea: Use a big “graph” to define relationships between words, it has
tree structure to declare the relationship between words.
Famous example: WordNet
Disadvantages:
Difficult to maintain(when new word comes in).
Require human labour.
Hard to compute word similarity.

55. Word Vectors-One Hot Representation

56. Word Vectors-Window Based Coocurrence-matrix
Problems:
Space consuming.
Difficult to update.
Solution:
Reduce dimension.(Singular
Value Decomposition)

57. Word Vectors-Word2vec
Word2vec: Predicts neighbor words.
Previous approach: capturing co-occurrence statistics.
Advantage:
Faster and can easily incorporate a new sentence/ document or add a
word to the vocabulary.
Good representation. (Solve analogy by vector subtraction)

58. Word Vectors-Word2vec
Error function:
(Where m is the window size. theta means all the parameters that we want to optimize.)

59. Word Vectors-Word2vec
Problem:
With large vocabularies this objective function is not scalable and
would train too slow.(use glove instead)
Solution:
Negative sampling.

60. Word Vectors-Word2vec

61. Word Vectors-Skip Gram Model
big window size may damage the syntactic accuracy.

62. Word Vectors-Continuous Bag of Words
Differ from word2vec, this model trying to predict the center word from the
surrounding words.
The result will be slightly different from skip-gram model, by average them we
can get a better result.

63. Word Vectors-Comparison

64. Word Vectors-Glove
Collect the co-occurrence statistics information from the whole corpus instead
of going over one window at a time.
Then optimize the vectors using the following equation.
Where Pij is the coocurrence counts from the matrix.
Fast training(do not have to go over every window), Scalable to huge corpora,
Good performance with small corpus.

65. Word Vectors-Glove Overview
Word-word Co-occurance Matrix, X : V * V (V is the vocab size)
Xij: the number of times word j occurs in the context of word i.
Xi = t : the number of times any word appears in the
context of word i.
Pi j = P(j|i) =Xi j/Xi : probability that word j appear in the context of word i.
P(solid | ice) = word “solid” appear in the context of word “ice”.
GloVe: Global Vectors for Word Representation

66. Symmetric
Word Vectors-GloVe
Ratios of co-occur: define a function:
Linearity:
Vector:

67. Word Vectors-GloVe
Add bias: log(Xi) independent from k,add as bi
Square error：

68. Word Vectors-GloVe: f(x) as weights for words
f(0)=0
monotonically increasing
large x, small f(x)
Usually,
xmax=100,α=3/4

69. Word Vectors-Evaluation Good

70. Recurrent Neural Network-Forward prop

71. Recurrent Neural Network-Forward prop

72. Recurrent Neural Network-Loss Function
The cross-entropy in one single time step:
Overall cross-entrophy cost:
Where V is the vocabulary and T means the text.
Exp:
yt = [0.3,0.6,0.1] the, a, movie
y1 = [0.001,0.009,0.9]
y2 = [0.001,0.299,0.7]
y3 = [0.001,0.9,0.009]
J1= yt*logJ1
J2= yt*logJ2
J3 = yt*logJ3
J3>J2>J1 because y3 is more close to
yt than others.

73. Recurrent Neural Network-Back Propagation

74. Recurrent Neural Network-Back Propagation
eg:

75. Recurrent Neural Network-Back Propagation

76. Recurrent Neural Network- Gradient Vanishing

77. Recurrent Neural Network-Clip gradient

78. SVD: Singular Value Decomposition
Starts from Matrix Multiplication: Y = A*B
Check codes and plots here.
Want to find the direction & extend:

79. SVD: Singular Value Decomposition
Eigen-Value & Eigen-Vector of A:
(Have more than one pairs. )
Import numpy to calculate. =>
But only for square matrix!

80. SVD: Singular Value Decomposition
If A has n e-values:
Then:
So, AQ=Q x Sigma
Q
Sigma
Q

81. SVD: Singular Value Decomposition
For the non-square matrix? A: m * n.
Similar idea:
But how to get e-values and e-vectors?

82. SVD: Singular Value Decomposition
Find a square-matrix!
Calculate… then:
let r << # of e-value to represent A
O(n^3)

83. SVD: Application
Copression with loss!
Reduce parameter size!
if m = 1,000 n = 1,000
let r = 10
10^6 reduced to 20100 parameters

84. MF: Matrix Factorization in RecSys
Different from SVD. In MF, we let Y = U V , divide into two matrices. We will
walk through with recommender system.
http://www.dataperspective.info/2014/05/basic-recommendation-engine-using-r.html
Movies
Ratings
Us
ers

85. MF: Matrix Factorization in RecSys
Rating (user i, movie j) = User i Vector · Movie j Vector
So how to find the User Matrix and Movie Matrix?
Movies
RatingsUsers
= User Matrix
Movie
Matrix
user i
movie j
Rij

86. MF: Matrix Factorization in RecSys
Predict rating of user i, movie j:
Loss function (error and L2 regularization):
So we want to minimize L and get U and M, using SGD:
argmin L
Once U and M are computed, we can predict any ratings!

87. Takeaway(1): Recognize Algorithms!
http://scikit-learn.org/stable/auto_examples/classification/plot_classifier_comparison.html

88. Takeaway(2): Recognize Algorithms- KNN

89. Useful Links
Stanford CS224d: Deep Learning for Natural Language Processing
Stanford CS231n: Convolutional Neural Networks for Visual Recognition
SVM Notes :http://www.robots.ox.ac.uk/~az/lectures/ml/lect2.pdf
Nuts and Bolts of Applying Deep Learning (Andrew Ng) - YouTube