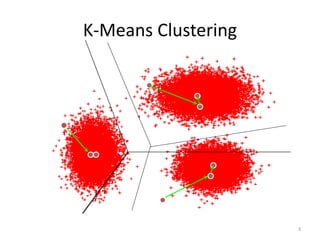
The document outlines the application of MapReduce to k-means clustering, detailing the process of assigning initial cluster centers, iteratively updating clusters, and finalizing the output. It discusses the Expectation-Maximization (EM) algorithm for parameter estimation in probabilistic models, highlighting the steps involved in maximizing the log-likelihood through iterative calculations. Additionally, the document introduces concepts related to probabilistic latent semantic analysis (PLSA), emphasizing the generative process for documents and terms using latent variables.

1. Machine Learning with MapReduce

3. K-Means Clustering
3

4. How to MapReduce K-Means?
• Given K, assign the first K random points to be
the initial cluster centers
• Assign subsequent points to the closest cluster
using the supplied distance measure
• Compute the centroid of each cluster and
iterate the previous step until the cluster
centers converge within delta
• Run a final pass over the points to cluster
them for output

5. K-Means Map/Reduce Design
• Driver
– Runs multiple iteration jobs using mapper+combiner+reducer
– Runs final clustering job using only mapper
• Mapper
– Configure: Single file containing encoded Clusters
– Input: File split containing encoded Vectors
– Output: Vectors keyed by nearest cluster
• Combiner
– Input: Vectors keyed by nearest cluster
– Output: Cluster centroid vectors keyed by “cluster”
• Reducer (singleton)
– Input: Cluster centroid vectors
– Output: Single file containing Vectors keyed by cluster

6. Mapper - mapper has k centers in memory.
Input Key-value pair (each input data point x).
Find the index of the closest of the k centers (call it iClosest).
Emit: (key,value) = (iClosest, x)
Reducer(s) – Input (key,value)
Key = index of center
Value = iterator over input data points closest to ith center
At each key value, run through the iterator and average all the
Corresponding input data points.
Emit: (index of center, new center)

7. Improved Version: Calculate partial sums in mappers
Mapper - mapper has k centers in memory. Running through one
input data point at a time (call it x). Find the index of the closest of the
k centers (call it iClosest). Accumulate sum of inputs segregated into
K groups depending on which center is closest.
Emit: ( , partial sum)
Or
Emit(index, partial sum)
Reducer – accumulate partial sums and
Emit with index or without

8. EM-Algorithm

9. What is MLE?
• Given
– A sample X={X1, …, Xn}
– A vector of parameters θ
• We define
– Likelihood of the data: P(X | θ)
– Log-likelihood of the data: L(θ)=log P(X|θ)
• Given X, find
)
(
max
arg 



L
ML



10. MLE (cont)
• Often we assume that Xis are independently identically
distributed (i.i.d.)
• Depending on the form of p(x|θ), solving optimization
problem can be easy or hard.
)
|
(
log
max
arg
)
|
(
log
max
arg
)
|
,...,
(
log
max
arg
)
|
(
log
max
arg
)
(
max
arg
1






















i
i
i
i
n
ML
X
P
X
P
X
X
P
X
P
L







11. An easy case
• Assuming
– A coin has a probability p of being heads, 1-p of
being tails.
– Observation: We toss a coin N times, and the
result is a set of Hs and Ts, and there are m Hs.
• What is the value of p based on MLE, given
the observation?

12. An easy case (cont)
)
1
log(
)
(
log
)
1
(
log
)
|
(
log
)
(
p
m
N
p
m
p
p
X
P
L m
N
m








 
0
1
))
1
log(
)
(
log
(
)
(










p
m
N
p
m
dp
p
m
N
p
m
d
dp
dL
p= m/N

13. Basic setting in EM
• X is a set of data points: observed data
• Θ is a parameter vector.
• EM is a method to find θML where
• Calculating P(X | θ) directly is hard.
• Calculating P(X,Y|θ) is much simpler, where Y is
“hidden” data (or “missing” data).
)
|
(
log
max
arg
)
(
max
arg








X
P
L
ML




14. The basic EM strategy
• Z = (X, Y)
– Z: complete data (“augmented data”)
– X: observed data (“incomplete” data)
– Y: hidden data (“missing” data)

15. The log-likelihood function
• L is a function of θ, while holding X constant:
)
|
(
)
(
)
|
( 

 X
P
L
X
L 

)
|
,
(
log
)
|
(
log
)
|
(
log
)
|
(
log
)
(
log
)
(
1
1
1






y
x
P
x
P
x
P
X
P
L
l
i
y
n
i
i
n
i
n
i
i













16. The iterative approach for MLE
)
|
,
(
log
max
arg
)
(
max
arg
)
(
max
arg
1





y
x
p
l
L
n
i y
i
ML
 












,....
,...,
, 1
0 t



In many cases, we cannot find the solution directly.
An alternative is to find a sequence:
....
)
(
...
)
(
)
( 1
0



 t
l
l
l 


s.t.

17. ]
)
|
,
(
)
|
,
(
[log
]
)
|
,
(
)
|
,
(
[
log
)
|
,
(
)
|
,
(
)
,
|
(
log
)
|
,
(
)
|
,
(
)
|
'
,
(
)
|
,
(
log
)
|
,
(
)
|
,
(
)
|
'
,
(
)
|
,
(
log
)
|
'
,
(
)
|
,
(
log
)
|
,
(
)
|
,
(
log
)
|
,
(
log
)
|
,
(
log
)
|
(
log
)
|
(
log
)
(
)
(
1
)
,
|
(
1
)
,
|
(
1
'
1
'
1
'
1
1
1
1
t
i
i
n
i
x
y
P
t
i
i
n
i
x
y
P
t
i
i
t
n
i y
i
t
i
i
y
t
y
i
t
i
n
i
t
i
t
i
y
t
y
i
i
n
i
y
t
y
i
i
n
i
t
y
i
y
i
n
i
t
y
i
n
i
y
i
n
i
t
t
y
x
P
y
x
P
E
y
x
P
y
x
P
E
y
x
P
y
x
P
x
y
P
y
x
P
y
x
P
y
x
P
y
x
P
y
x
P
y
x
P
y
x
P
y
x
P
y
x
P
y
x
P
y
x
P
y
x
P
y
x
P
y
x
P
X
P
X
P
l
l
t
i
t
i





























 







































Jensen’s inequality

18. Jensen’s inequality
])
(
[
(
)]
(
(
[
, x
g
E
f
x
g
f
E
then
convex
is
f
if 


)])
(
[
log(
)]
(
[log( x
p
E
x
p
E 
])
(
[
(
)]
(
(
[
, x
g
E
f
x
g
f
E
then
concave
is
f
if 


log is a concave function

19. Maximizing the lower bound
)]
|
,
(
[log
max
arg
)
|
,
(
log
)
,
|
(
max
arg
)
|
,
(
)
|
,
(
log
)
,
|
(
max
arg
]
)
|
,
(
)
|
,
(
[log
max
arg
1
)
,
|
(
1
1
1
)
,
|
(
)
1
(















y
x
P
E
y
x
P
x
y
P
y
x
P
y
x
P
x
y
P
y
x
p
y
x
p
E
i
n
i
x
y
P
i
t
i
n
i y
t
i
i
t
i
n
i y
t
i
i
n
i
x
y
P
t
t
i
t
i













The Q function

20. The Q-function
• Define the Q-function (a function of θ):
– Y is a random vector.
– X=(x1, x2, …, xn) is a constant (vector).
– Θt is the current parameter estimate and is a constant (vector).
– Θ is the normal variable (vector) that we wish to adjust.
• The Q-function is the expected value of the complete data log-likelihood
P(X,Y|θ) with respect to Y given X and θt.
)
|
,
(
log
)
,
|
(
)]
|
,
(
[log
)
|
,
(
log
)
,
|
(
)]
|
,
(
[log
]
,
|
)
|
,
(
[log
)
,
(
1
1
)
,
|
(
)
,
|
(












y
x
P
x
y
P
y
x
P
E
Y
X
P
X
Y
P
Y
X
P
E
X
Y
X
P
E
Q
i
t
n
i y
i
n
i
i
x
y
P
Y
t
X
Y
P
t
t
t
i
t











21. The inner loop of the
EM algorithm
• E-step: calculate
• M-step: find
)
,
(
max
arg
)
1
( t
t
Q 





)
|
,
(
log
)
,
|
(
)
,
(
1



 y
x
P
x
y
P
Q i
t
n
i y
i
t




22. L(θ) is non-decreasing
at each iteration
• The EM algorithm will produce a sequence
• It can be proved that
,....
,...,
, 1
0 t



....
)
(
...
)
(
)
( 1
0



 t
l
l
l 



23. The inner loop of the
Generalized EM algorithm (GEM)
• E-step: calculate
• M-step: find
)
,
(
max
arg
)
1
( t
t
Q 





)
|
,
(
log
)
,
|
(
)
,
(
1



 y
x
P
x
y
P
Q i
t
n
i y
i
t



)
,
(
)
,
( 1 t
t
t
t
Q
Q 


 


24. Recap of the EM algorithm

25. Idea #1: find θ that maximizes the
likelihood of training data
)
|
(
log
max
arg
)
(
max
arg








X
P
L
ML




26. Idea #2: find the θt sequence
No analytical solution  iterative approach, find
s.t.
,....
,...,
, 1
0 t



....
)
(
...
)
(
)
( 1
0



 t
l
l
l 



27. Idea #3: find θt+1 that maximizes a tight
lower bound of )
(
)
( t
l
l 
 
a tight lower bound
]
)
|
,
(
)
|
,
(
[log
)
(
)
(
1
)
,
|
( t
i
i
n
i
x
y
P
t
y
x
P
y
x
P
E
l
l t
i



 





28. Idea #4: find θt+1 that maximizes
the Q function
)]
|
,
(
[log
max
arg
]
)
|
,
(
)
|
,
(
[log
max
arg
1
)
,
|
(
1
)
,
|
(
)
1
(








y
x
P
E
y
x
p
y
x
p
E
i
n
i
x
y
P
t
i
i
n
i
x
y
P
t
t
i
t
i







Lower bound of )
(
)
( t
l
l 
 
The Q function

29. The EM algorithm
• Start with initial estimate, θ0
• Repeat until convergence
– E-step: calculate
– M-step: find
)
,
(
max
arg
)
1
( t
t
Q 





)
|
,
(
log
)
,
|
(
)
,
(
1



 y
x
P
x
y
P
Q i
t
n
i y
i
t




30. Important classes of EM problem
• Products of multinomial (PM) models
• Exponential families
• Gaussian mixture
• …

31. Probabilistic Latent Semantic Analysis (PLSA
• PLSA is a generative model for generating the co-
occurrence of documents d∈D={d1,…,dD} and terms
w∈W={w1,…,wW}, which associates latent variable
z∈Z={z1,…,zZ}.
• The generative processing is:
w1
w2
wW
…
d1
d2
dD
…
z1
z2
zZ
P(d)
P(z|d)
P(w|z)

32. Model
• The generative process can be expressed by:
( , ) ( ) ( | ),
( | ) ( | ) ( | )
z Z
P d w P d P w d
where P w d P w z P z d


  
Two independence assumptions:
1) Each pair (d,w) are assumed to be generated independently,
corresponding to ‘bag-of-words’
2) Conditioned on z, words w are generated independently of the
specific document d.

33. Model
• Following the likelihood principle, we detemines P(z),
P(d|z), and P(w|z) by maximization of the log-
likelihood function
( | , , ) ( , )log ( , )
d D w W
L d w z n d w P d w
 
  
( , ) ( | ) ( | ) ( ) ( | ) ( | ) ( )
z Z z Z
where P d w P w z P z d P d P w z P d z P z
 
 
 
co-occurrence
times of d and w.
Observed data
Unobserved
data
P(d), P(z|d),
and P(w|d)

34. Maximum-likelihood
• Definition
– We have a density function P(x|Θ) that is govened by the set of
parameters Θ, e.g., P might be a set of Gaussians and Θ could be the
means and covariances
– We also have a data set X={x1,…,xN}, supposedly drawn from this
distribution P, and assume these data vectors are i.i.d. with P.
– Then the likehihood function is:
– The likelihood is thought of as a function of the parameters Θwhere
the data X is fixed. Our goal is to find the Θthat maximizes L. That is
1
( | ) ( | ) ( | )
N
i
i
P X P x L X

    

*
argmax ( | )
L X

  

35. Jensen’s inequality
0
)
(
0
1
)
(
)
(





 
j
g
a
a
provided
j
g
a
j
g
j
j
j
j j
a
j
j

36.  
  


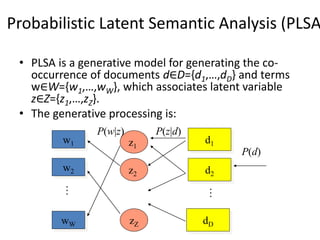
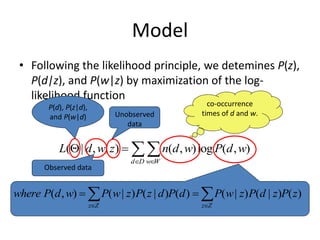
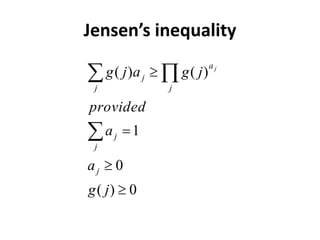
D
d W
w Z
z
z
d
P
z
w
P
z
P
w
d
n
z
w
d
L )
|
(
)
|
(
)
(
log
)
,
(
max
)
,
,
|
(
max
Estimation-using EM
difficult!!!
Idea: start with a guess t, compute an easily computed lower-bound B(; t)
to the function log P(|U) and maximize the bound instead
By Jensen’s inequality:
)
,
|
(
]
)
,
|
(
)
|
(
)
|
(
)
(
[
)
,
|
(
)
,
|
(
)
|
(
)
|
(
)
(
d
w
z
P
Z
z j d
w
z
P
z
d
P
z
w
P
z
P
d
w
z
P
d
w
z
P
z
d
P
z
w
P
z
P
 


 


 
 





D
d W
w z
d
w
z
P
z
D
d W
w
t
d
w
z
P
d
w
z
P
z
d
P
z
w
P
z
P
w
d
n
d
w
z
P
z
d
P
z
w
P
z
P
w
d
n
B
)
,
|
(
)]
,
|
(
log
)
|
(
)
|
(
)
(
[log
)
,
(
max
]
)
,
|
(
)
|
(
)
|
(
)
(
[
log
)
,
(
max
)
,
(
max
)
,
|
(

37. (1)Solve P(w|z)
• We introduce Lagrange multiplier λwith the constraint that
∑wP(w|z)=1, and solve the following equation:
( , ) [log ( ) ( | ) ( | ) log ( | , )] ( | , ) ( ( | ) 1) 0
( | )
( , ) ( | , )
0,
( | )
( , ) ( | , )
( | ) ,
( | ) 1,
( , ) ( | , ),
( , )
( | )
d D w W z w
d D
d D
w
w W d D
n d w P z P w z P d z P z w d P z w d P w z
P w z
n d w P z d w
P w z
n d w P z d w
P w z
P w z
n d w P z d w
n d w P
P w z




 


 
  
   
 
  
  
  

  
 
   



 
( | , )
( , ) ( | , )
d D
w W d D
z d w
n d w P z d w

 

 

38. (2)Solve P(d|z)
• We introduce Lagrange multiplier λwith the constraint that
∑dP(d|z)=1, and get the following result:
( , ) ( | , )
( | )
( , ) ( | , )
w W
d D w W
n d w P z d w
P d z
n d w P z d w

 
 

 

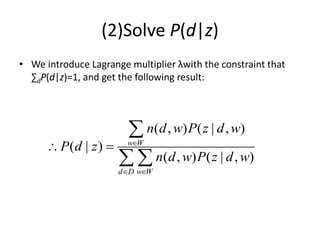
39. (3)Solve P(z)
• We introduce Lagrange multiplier λwith the constraint that
∑zP(z)=1, and solve the following equation:
( , ) [log ( ) ( | ) ( | ) log ( | , )] ( | , ) ( ( ) 1) 0
( )
( , ) ( | , )
0,
( )
( , ) ( | , )
( ) ,
( ) 1,
( , ) ( | , ) ( , ),
d D w W z z
d D w W
d D w W
z
d D w W z d D w W
n d w P z P w z P d z P z w d P z w d P z
P z
n d w P z d w
P z
n d w P z d w
P z
P z
n d w P z d w n d w




 
 
 
   
  
   
 
  
  
  

    
   
 
 

   
( , ) ( | , )
( )
( , )
d D w W
w W d D
n d w P z d w
P z
n d w
 
 
 

 
 

40. (1)Solve P(z|d,w)
• We introduce Lagrange multiplier λwith the constraint that
∑zP(z|d,w)=1, and solve the following equation:
,
,
,
( , ) [log ( ) ( | ) ( | ) log ( | , )] ( | , ) ( ( | , ) 1) 0
( | , )
( , )[log ( ) ( | ) ( | ) log ( | , ) 1] 0,
log ( | , ) log ( ) ( | ) ( | ) 1 0,
( |
d w
d D w W z d D w W z
d w
d w
n d w P z P w z P d z P z d w P z d w P z d w
P z d w
n d w P z P w z P d z P z d w
P z d w P z P w z P d z
P z d



   
  
   
 
  
    
    

     
,
,
,
1
1
,
1
1 (1 log ( ) ( | ) ( | ))
, ) ( ) ( | ) ( | )
( | , ) 1,
( ) ( | ) ( | ) 1
1 log ( ) ( | ) ( | )
( ) ( | ) ( | )
( | )
( ) ( | ) ( | )
( ) ( | ) ( | )
( ) ( |
d w
d w
d w
z
z
z
d w
z
P z P w z P d z
w P z P w z P d z e
P z d w
P z P w z P d z e
P z P w z P d z
P z P w z P d z
P w z
e
P z P w z P d z
e
P z P w z P d z
P z P w z







 


 
  
 






) ( | )
z
P d z


41. (4)Solve P(z|d,w) -2
( , , )
( | , )
( , )
( , | ) ( )
( , )
( | ) ( | ) ( )
( | ) ( | ) ( )
z Z
P d w z
P z d w
P d w
P w d z P z
P d w
P w z P d z P z
P w z P d z P z






42. The final update Equations
• E-step:
• M-step:
( | ) ( | ) ( )
( | , )
( | ) ( | ) ( )
z Z
P w z P d z P z
P z d w
P w z P d z P z



( , ) ( | , )
( | )
( , ) ( | , )
d D
w W d D
n d w P z d w
P w z
n d w P z d w

 



( , ) ( | , )
( | )
( , ) ( | , )
w W
d D w W
n d w P z d w
P d z
n d w P z d w

 



( , ) ( | , )
( )
( , )
d D w W
w W d D
n d w P z d w
P z
n d w
 
 




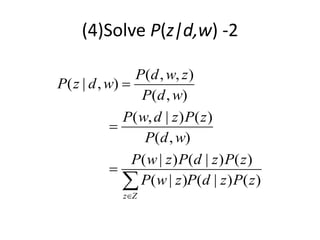
43. Coding Design
• Variables:
• double[][] p_dz_n // p(d|z), |D|*|Z|
• double[][] p_wz_n // p(w|z), |W|*|Z|
• double[] p_z_n // p(z), |Z|
• Running Processing:
1. Read dataset from file
ArrayList<DocWordPair> doc; // all the docs
DocWordPair – (word_id, word_frequency_in_doc)
2. Parameter Initialization
Assign each elements of p_dz_n, p_wz_n and p_z_n with a random double value, satisfying
∑d p_dz_n=1, ∑d p_wz_n =1, and ∑d p_z_n =1
3. Estimation (Iterative processing)
1. Update p_dz_n, p_wz_n and p_z_n
2. Calculate Log-likelihood function to see where ( |Log-likelihood – old_Log-likelihood|
< threshold)
4. Output p_dz_n, p_wz_n and p_z_n

44. Coding Design
• Update p_dz_n
For each doc d{
For each word w included in d {
denominator = 0;
nominator = new double[Z];
For each topic z {
nominator[z] = p_dz_n[d][z]* p_wz_n[w][z]* p_z_n[z]
denominator +=nominator[z];
} // end for each topic z
For each topic z {
P_z_condition_d_w = nominator[j]/denominator;
nominator_p_dz_n[d][z] += tfwd*P_z_condition_d_w;
denominator_p_dz_n[z] += tfwd*P_z_condition_d_w;
} // end for each topic z
}// end for each word w included in d
}// end for each doc d
For each doc d {
For each topic z {
p_dz_n_new[d][z] = nominator_p_dz_n[d][z]/ denominator_p_dz_n[z];
} // end for each topic z
}// end for each doc d

45. Coding Design
• Update p_wz_n
For each doc d{
For each word w included in d {
denominator = 0;
nominator = new double[Z];
For each topic z {
nominator[z] = p_dz_n[d][z]* p_wz_n[w][z]* p_z_n[z]
denominator +=nominator[z];
} // end for each topic z
For each topic z {
P_z_condition_d_w = nominator[j]/denominator;
nominator_p_wz_n[w][z] += tfwd*P_z_condition_d_w;
denominator_p_wz_n[z] += tfwd*P_z_condition_d_w;
} // end for each topic z
}// end for each word w included in d
}// end for each doc d
For each w {
For each topic z {
p_wz_n_new[w][z] = nominator_p_wz_n[w][z]/ denominator_p_wz_n[z];
} // end for each topic z
}// end for each doc d

46. Coding Design
• Update p_z_n
For each doc d{
For each word w included in d {
denominator = 0;
nominator = new double[Z];
For each topic z {
nominator[z] = p_dz_n[d][z]* p_wz_n[w][z]* p_z_n[z]
denominator +=nominator[z];
} // end for each topic z
For each topic z {
P_z_condition_d_w = nominator[j]/denominator;
nominator_p_z_n[z] += tfwd*P_z_condition_d_w;
} // end for each topic z
denominator_p_z_n[z] += tfwd;
}// end for each word w included in d
}// end for each doc d
For each topic z{
p_dz_n_new[d][j] = nominator_p_z_n[z]/ denominator_p_z_n;
} // end for each topic z

47. Apache Mahout
Industrial Strength Machine Learning
GraphLab

48. Current Situation
• Large volumes of data are now available
• Platforms now exist to run computations over
large datasets (Hadoop, HBase)
• Sophisticated analytics are needed to turn data
into information people can use
• Active research community and proprietary
implementations of “machine learning”
algorithms
• The world needs scalable implementations of ML
under open license - ASF

49. History of Mahout
• Summer 2007
– Developers needed scalable ML
– Mailing list formed
• Community formed
– Apache contributors
– Academia & industry
– Lots of initial interest
• Project formed under Apache Lucene
– January 25, 2008

50. Current Code Base
• Matrix & Vector library
– Memory resident sparse & dense implementations
• Clustering
– Canopy
– K-Means
– Mean Shift
• Collaborative Filtering
– Taste
• Utilities
– Distance Measures
– Parameters

51. Others
• Naïve Bayes
• Perceptron
• PLSI/EM
• Genetic Programming
• Dirichlet Process Clustering
• Clustering Examples
• Hama (Incubator) for very large arrays