Recommended
PDF
PDF
PDF
PDF
【博士論文発表会】パラメータ制約付き特異モデルの統計的学習理論
PDF
PDF
PDF
明治大学講演資料「機械学習と自動ハイパーパラメタ最適化」 佐野正太郎
PDF
PDF
SSII2021 [OS2-01] 転移学習の基礎:異なるタスクの知識を利用するための機械学習の方法
PDF
機械学習による統計的実験計画(ベイズ最適化を中心に)
PPTX
[DL輪読会]Temporal DifferenceVariationalAuto-Encoder
PDF
[DL輪読会]Control as Inferenceと発展
PPTX
PPTX
[DL輪読会]Set Transformer: A Framework for Attention-based Permutation-Invariant...
PDF
PDF
PDF
PPTX
PPTX
PDF
PDF
PDF
PDF
PDF
PDF
PDF
はじめてのパターン認識 第5章 k最近傍法(k_nn法)
PDF
PDF
PDF
PDF
More Related Content
PDF
PDF
PDF
PDF
【博士論文発表会】パラメータ制約付き特異モデルの統計的学習理論
PDF
PDF
PDF
明治大学講演資料「機械学習と自動ハイパーパラメタ最適化」 佐野正太郎
PDF
What's hot
PDF
SSII2021 [OS2-01] 転移学習の基礎:異なるタスクの知識を利用するための機械学習の方法
PDF
機械学習による統計的実験計画(ベイズ最適化を中心に)
PPTX
[DL輪読会]Temporal DifferenceVariationalAuto-Encoder
PDF
[DL輪読会]Control as Inferenceと発展
PPTX
PPTX
[DL輪読会]Set Transformer: A Framework for Attention-based Permutation-Invariant...
PDF
PDF
PDF
PPTX
PPTX
PDF
PDF
PDF
PDF
PDF
PDF
PDF
はじめてのパターン認識 第5章 k最近傍法(k_nn法)
PDF
PDF
Similar to PCAの最終形態GPLVMの解説
PDF
PDF
PPTX
PDF
Math in Machine Learning / PCA and SVD with Applications
PDF
PDF
PPTX
第13回 KAIM 金沢人工知能勉強会 混合した信号を分解する視点からみる主成分分析
PDF
関東CV勉強会 Kernel PCA (2011.2.19)
PDF
PFI Christmas seminar 2009
PDF
PDF
PPTX
PDF
PDF
palla et al, a nonparametric variable clustering method
PDF
LCCC2010:Learning on Cores, Clusters and Cloudsの解説
PDF
PDF
PDF
データに隠れた構造を推定して予測に活かす 〜行列分解とそのテストスコアデータへの応用〜
PDF
El text.tokuron a(2019).yamamoto190627
PDF
CMSI計算科学技術特論A (2015) 第11回 行列計算における高速アルゴリズム2
More from 弘毅 露崎
PDF
PDF
文献注釈情報MeSHを利用した網羅的な遺伝子の機能アノテーションパッケージ
PDF
PDF
大規模テンソルデータに適用可能なeinsumの開発
PDF
PDF
LRBase × scTensorで細胞間コミュニケーションの検出
PDF
PDF
バイオインフォ分野におけるtidyなデータ解析の最新動向
PDF
Benchmarking principal component analysis for large-scale single-cell RNA-seq...
PDF
PDF
非負値テンソル分解を用いた細胞間コミュニケーション検出
PDF
PDF
Exploring the phenotypic consequences of tissue specific gene expression vari...
PDF
PDF
PDF
PDF
PDF
Identification of associations between genotypes and longitudinal phenotypes ...
PDF
A novel method for discovering local spatial clusters of genomic regions with...
PDF
Predicting drug-induced transcriptome responses of a wide range of human cell...
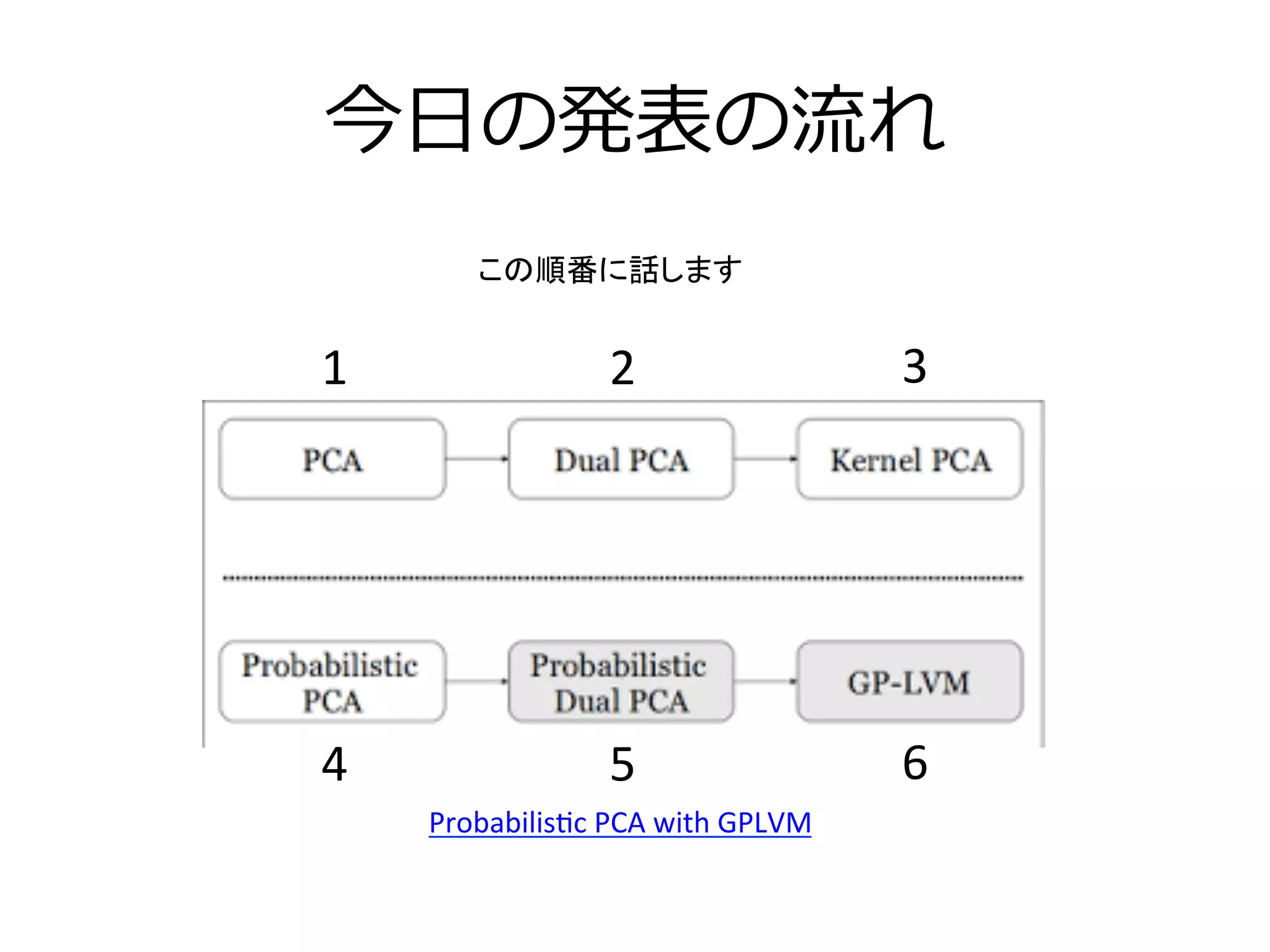
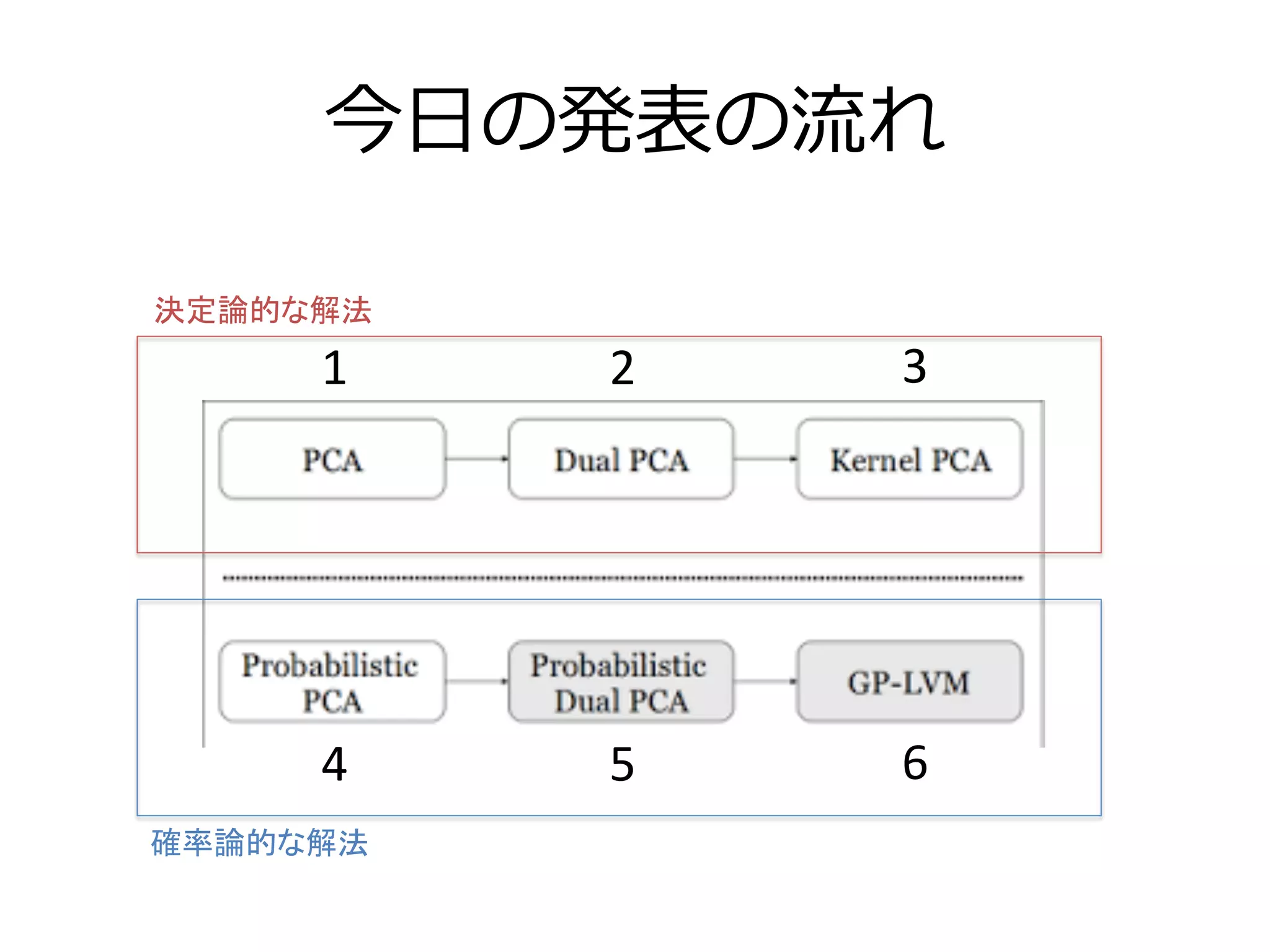
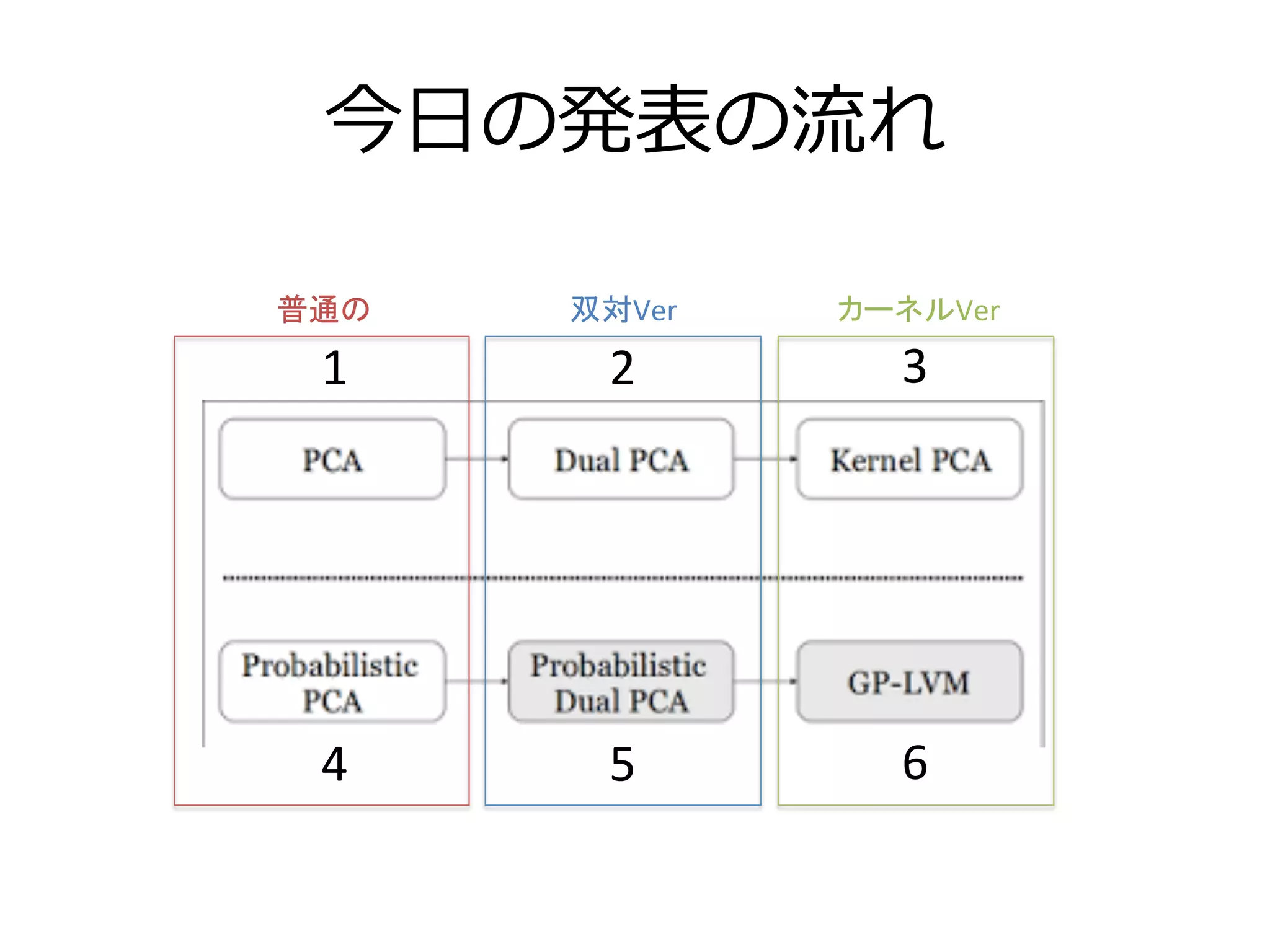
PCAの最終形態GPLVMの解説 1. 2. 3. 4. 5. 6. 7. 8. 考える上でのポイント
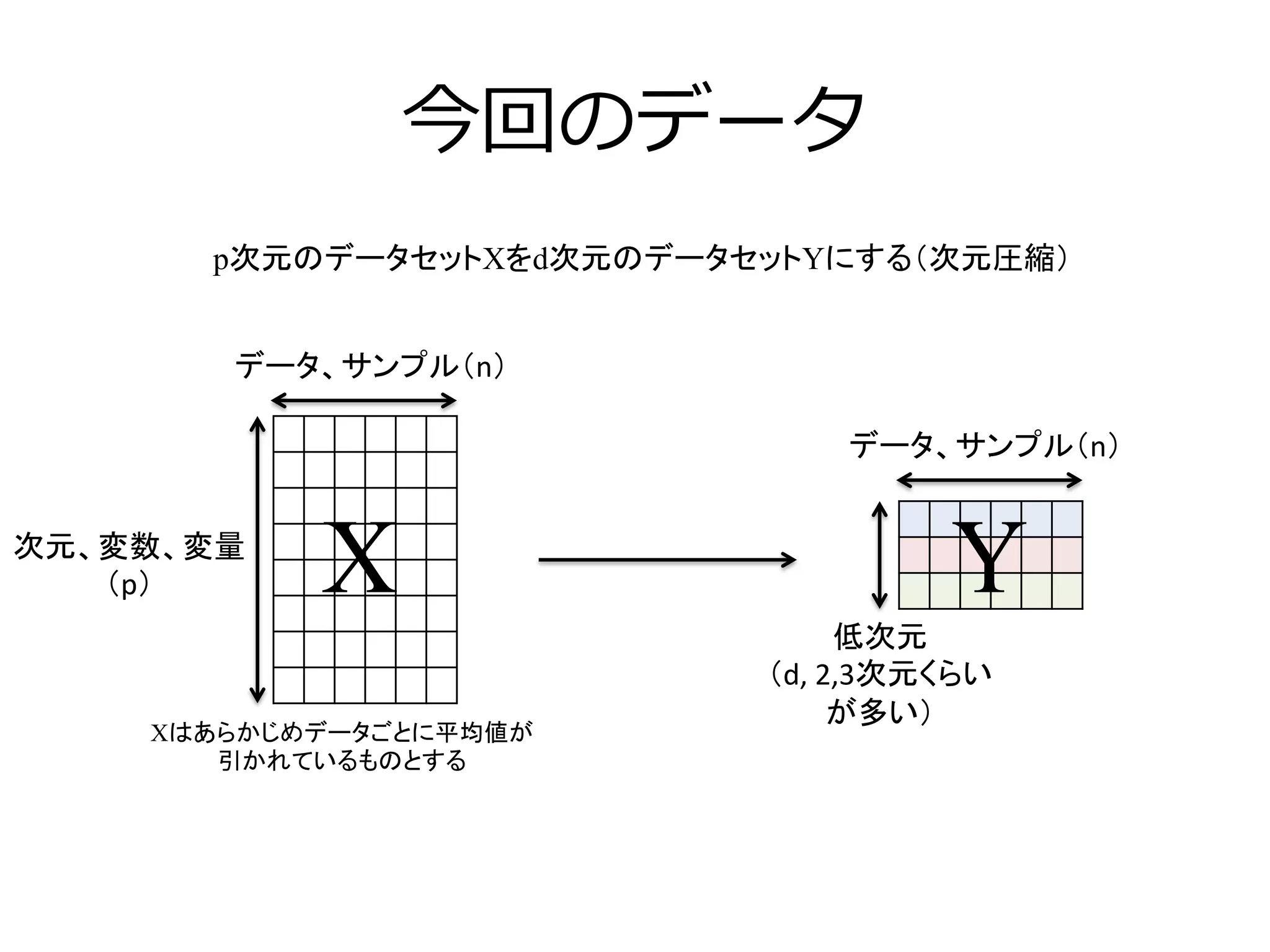
n
p
X
n
p
X
XT
p
n
=
=
XT
n
p
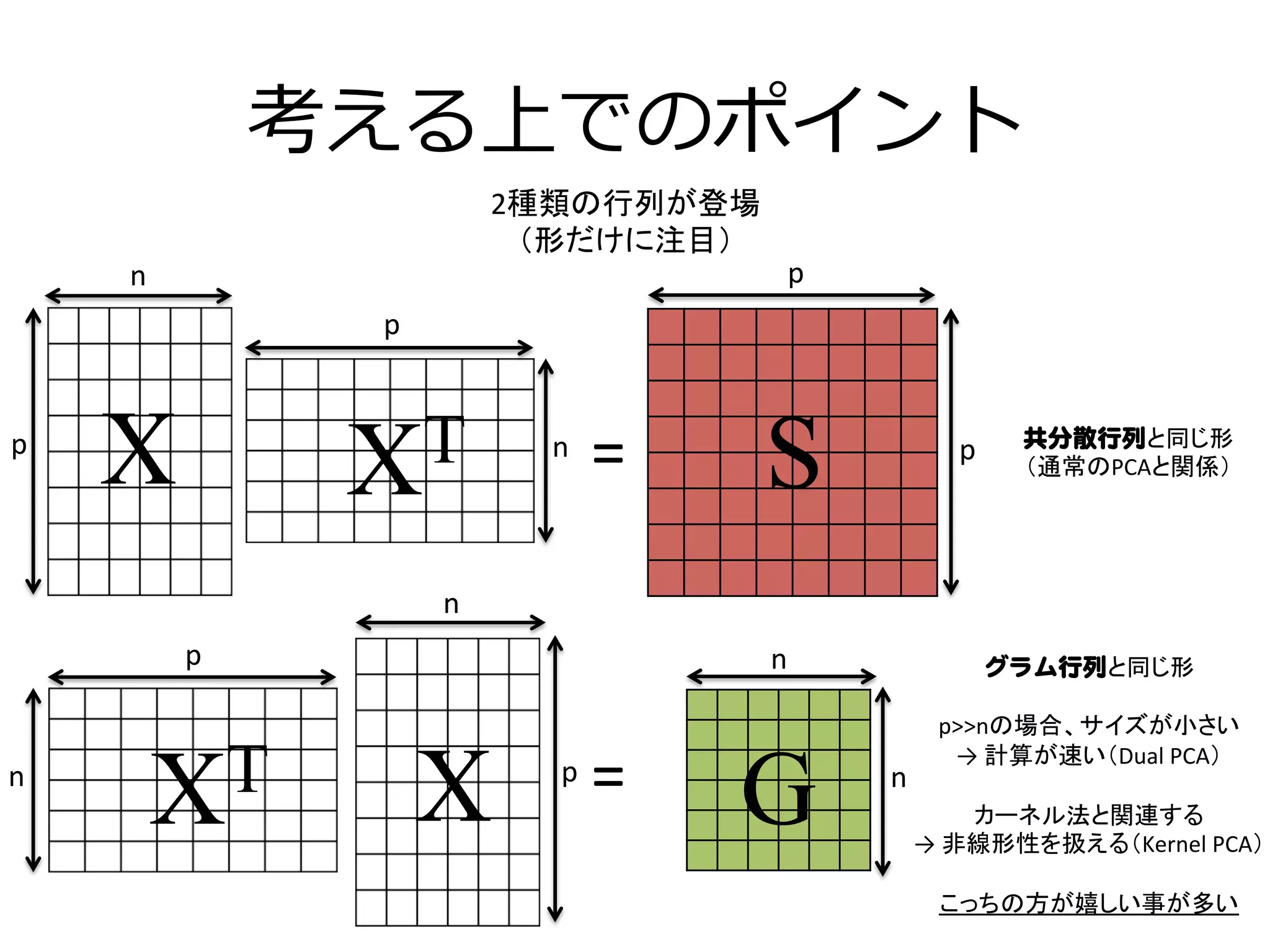
2種類の行列が登場
(形だけに注目)
n
n
p
p
S
G
グラム行列と同じ形
p>>nの場合、サイズが小さい
→
計算が速い(Dual
PCA)
カーネル法と関連する
→
非線形性を扱える(Kernel
PCA)
こっちの方が嬉しい事が多い
共分散行列と同じ形
(通常のPCAと関係)
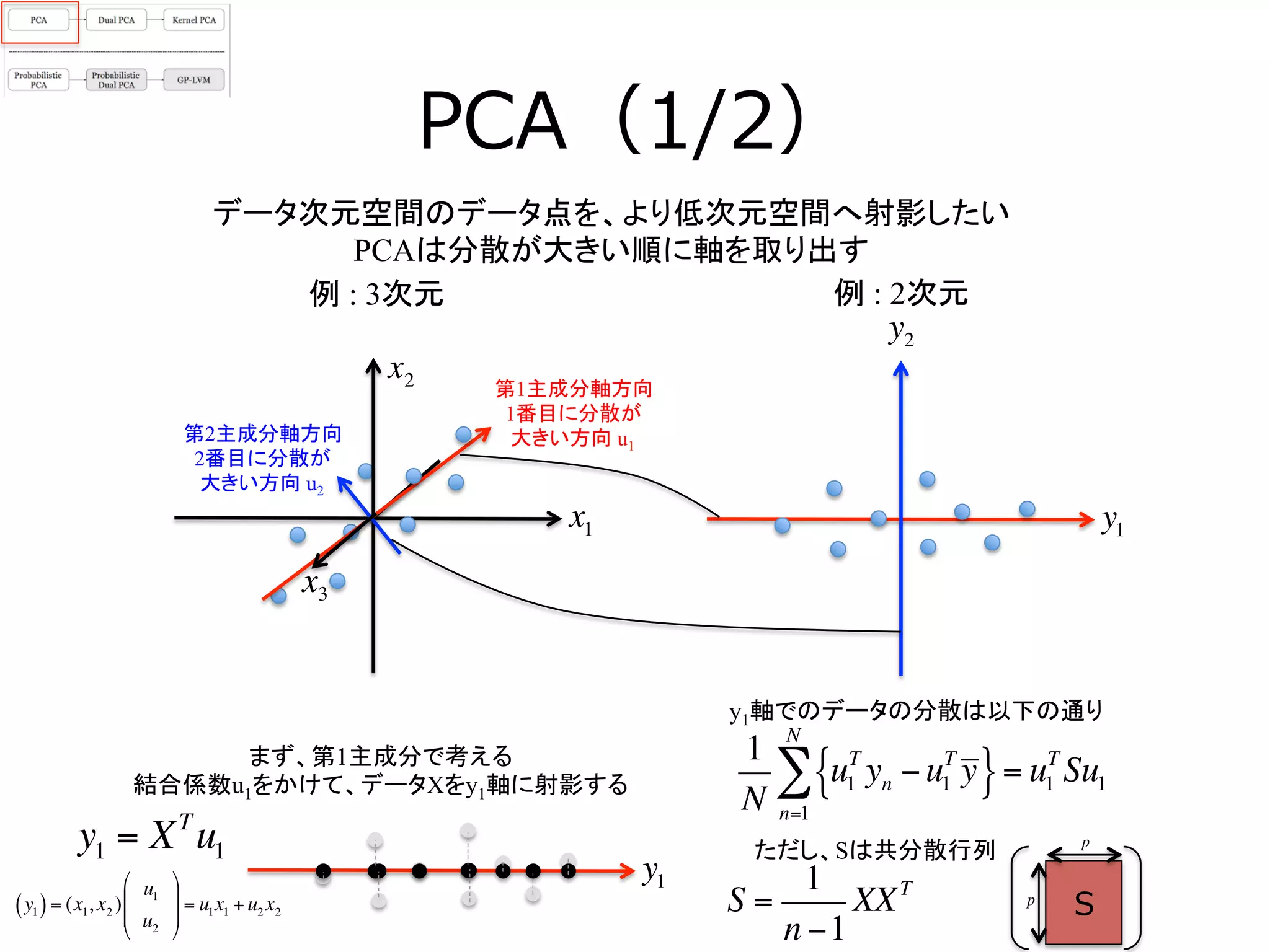
9. 10. PCA(1/2)
y1
データ次元空間のデータ点を、より低次元空間へ射影したい
PCAは分散が大きい順に軸を取り出す
例 : 3次元
例 : 2次元
y2
x3
x1
x2 第1主成分軸方向
1番目に分散が
大きい方向 u1
第2主成分軸方向
2番目に分散が
大きい方向 u2
まず、第1主成分で考える
結合係数u1をかけて、データXをy1軸に射影する
y1 = XT
u1
y1
y1軸でのデータの分散は以下の通り
1
N
u1
T
yn −u1
T
y{ }
n=1
N
∑ = u1
T
Su1
ただし、Sは共分散行列
Sp
p
S =
1
n −1
XXT
y1( )= (x1, x2 )
u1
u2
!
"
#
#
$
%
&
&
= u1x1 +u2 x2
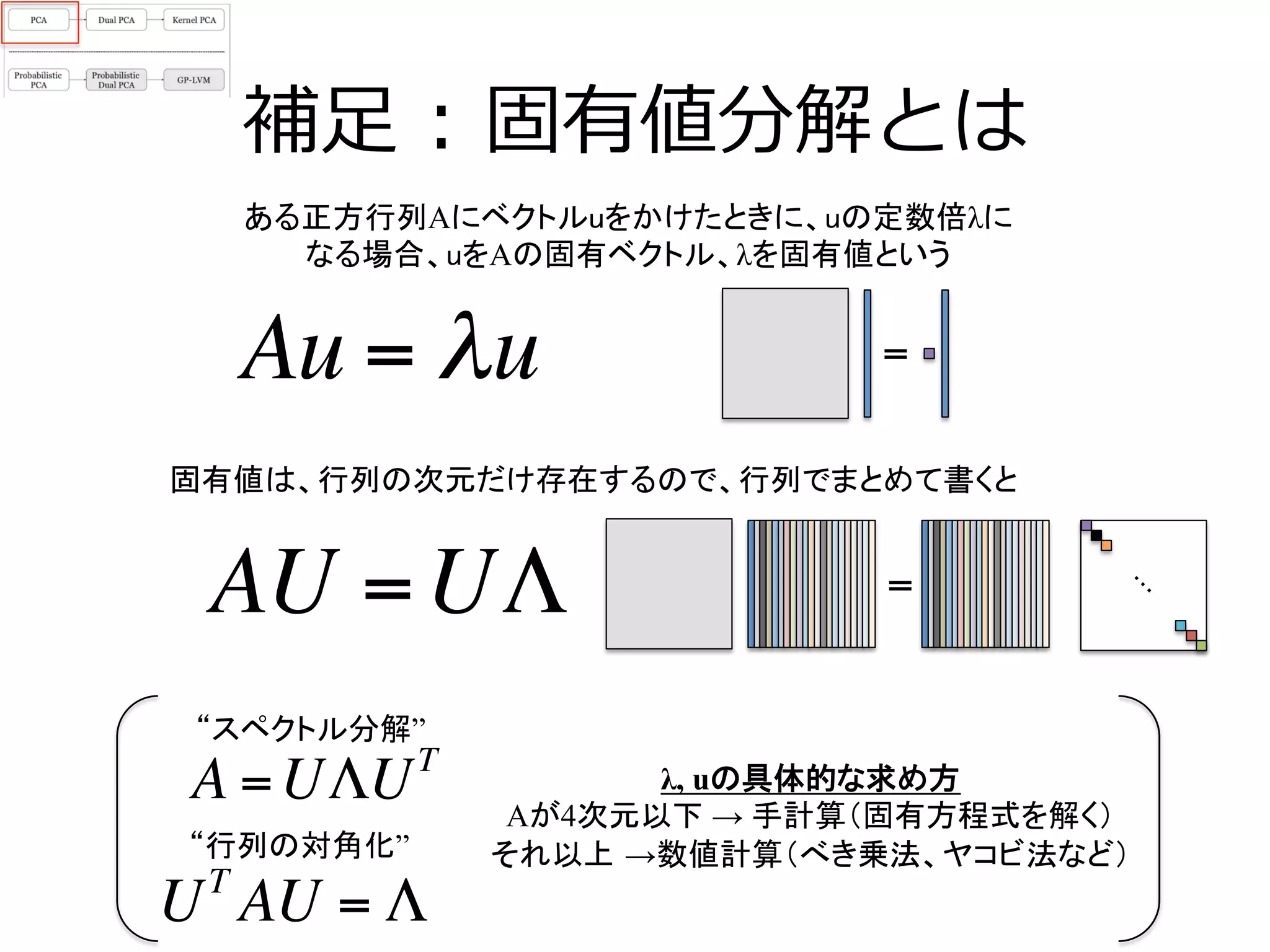
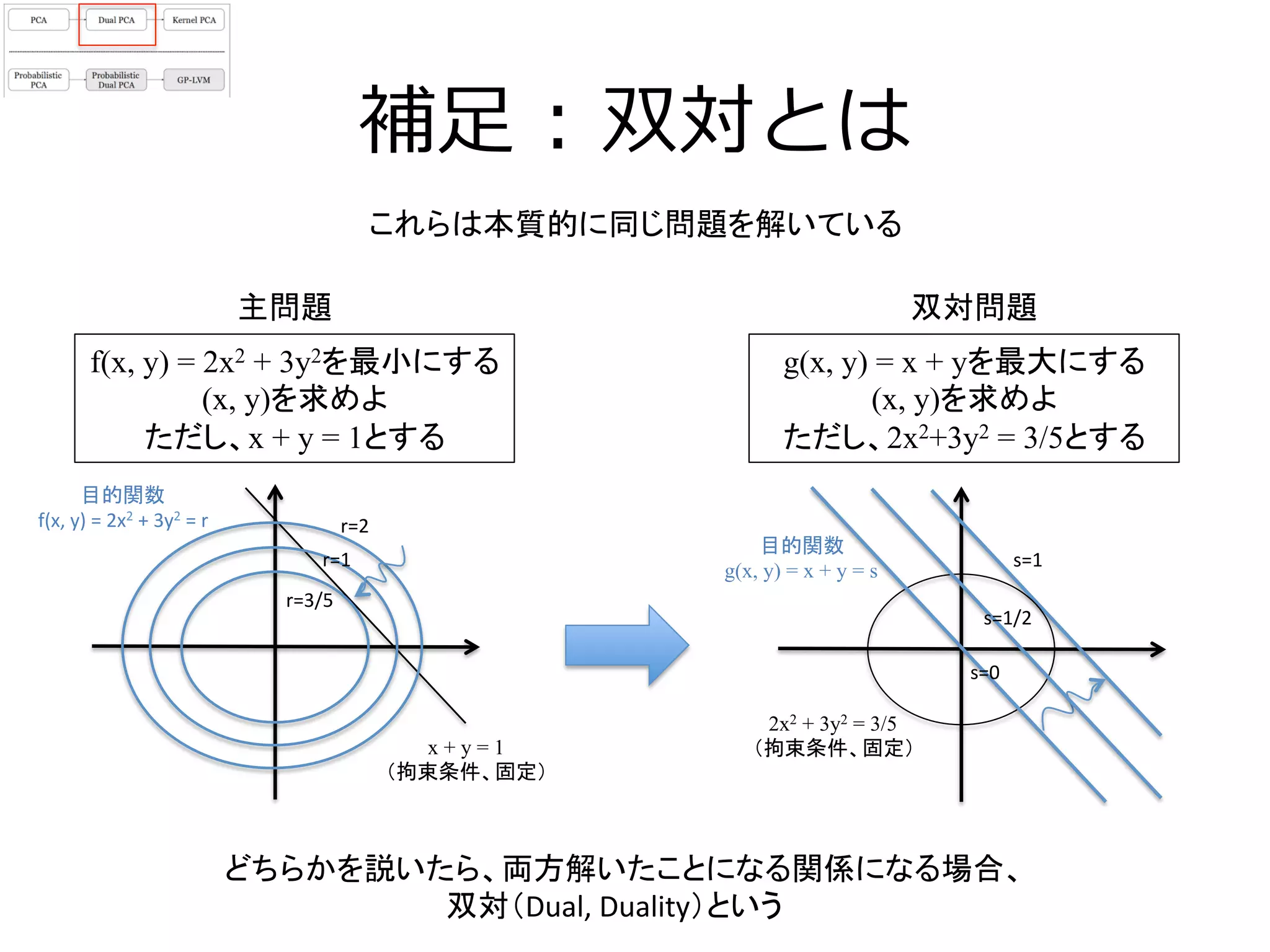
11. 12. 補⾜足 : 双対とは
双対問題
f(x, y) = 2x2 + 3y2を最小にする
(x, y)を求めよ
ただし、x + y = 1とする
g(x, y) = x + yを最大にする
(x, y)を求めよ
ただし、2x2+3y2 = 3/5とする
x + y = 1
(拘束条件、固定)
r=3/5
r=1
r=2
目的関数
g(x, y) = x + y = s
2x2 + 3y2 = 3/5
(拘束条件、固定)
目的関数
f(x,
y)
=
2x2
+
3y2
=
r
s=0
s=1/2
s=1
どちらかを説いたら、両方解いたことになる関係になる場合、
双対(Dual,
Duality)という
主問題
これらは本質的に同じ問題を解いている
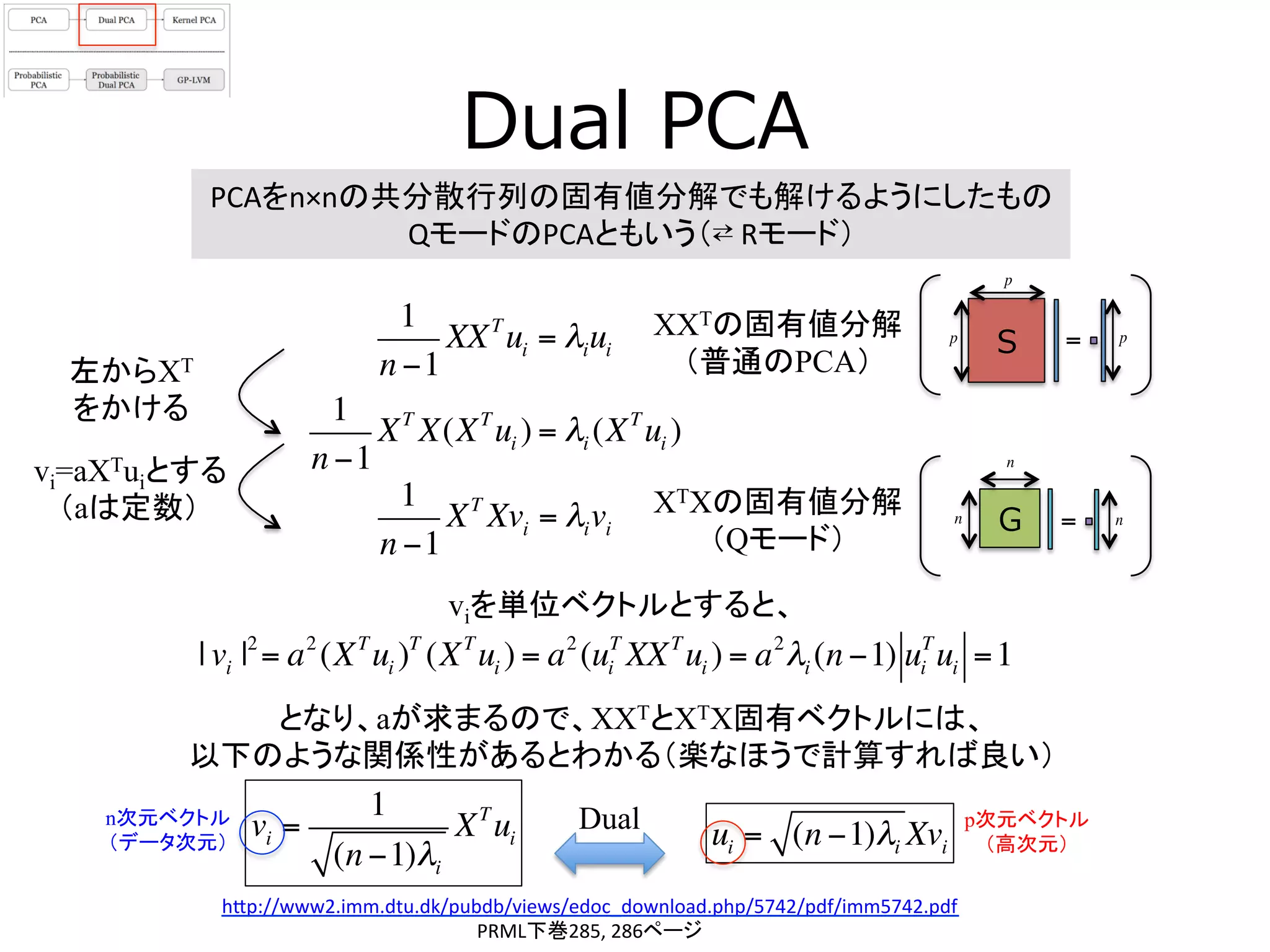
13. Dual PCA
PCAをn×nの共分散行列の固有値分解でも解けるようにしたもの
QモードのPCAともいう(⇄
Rモード)
h[p://www2.imm.dtu.dk/pubdb/views/edoc_download.php/5742/pdf/imm5742.pdf
PRML下巻285,
286ページ
1
n −1
XXT
ui = λiui
XXTの固有値分解
(普通のPCA)
1
n −1
XT
X(XT
ui ) = λi (XT
ui )
左からXT
をかける
XTXの固有値分解
(Qモード)
1
n −1
XT
Xvi = λivi
viを単位ベクトルとすると、
vi=aXTuiとする
(aは定数)
| vi |2
= a2
(XT
ui )T
(XT
ui ) = a2
(ui
T
XXT
ui ) = a2
λi (n −1) ui
T
ui =1
vi =
1
(n −1)λi
XT
ui
となり、aが求まるので、XXTとXTX固有ベクトルには、
以下のような関係性があるとわかる(楽なほうで計算すれば良い)
ui = (n −1)λi Xvi
S =p p
p
G =n n
n
Dualn次元ベクトル
(データ次元)
p次元ベクトル
(高次元)
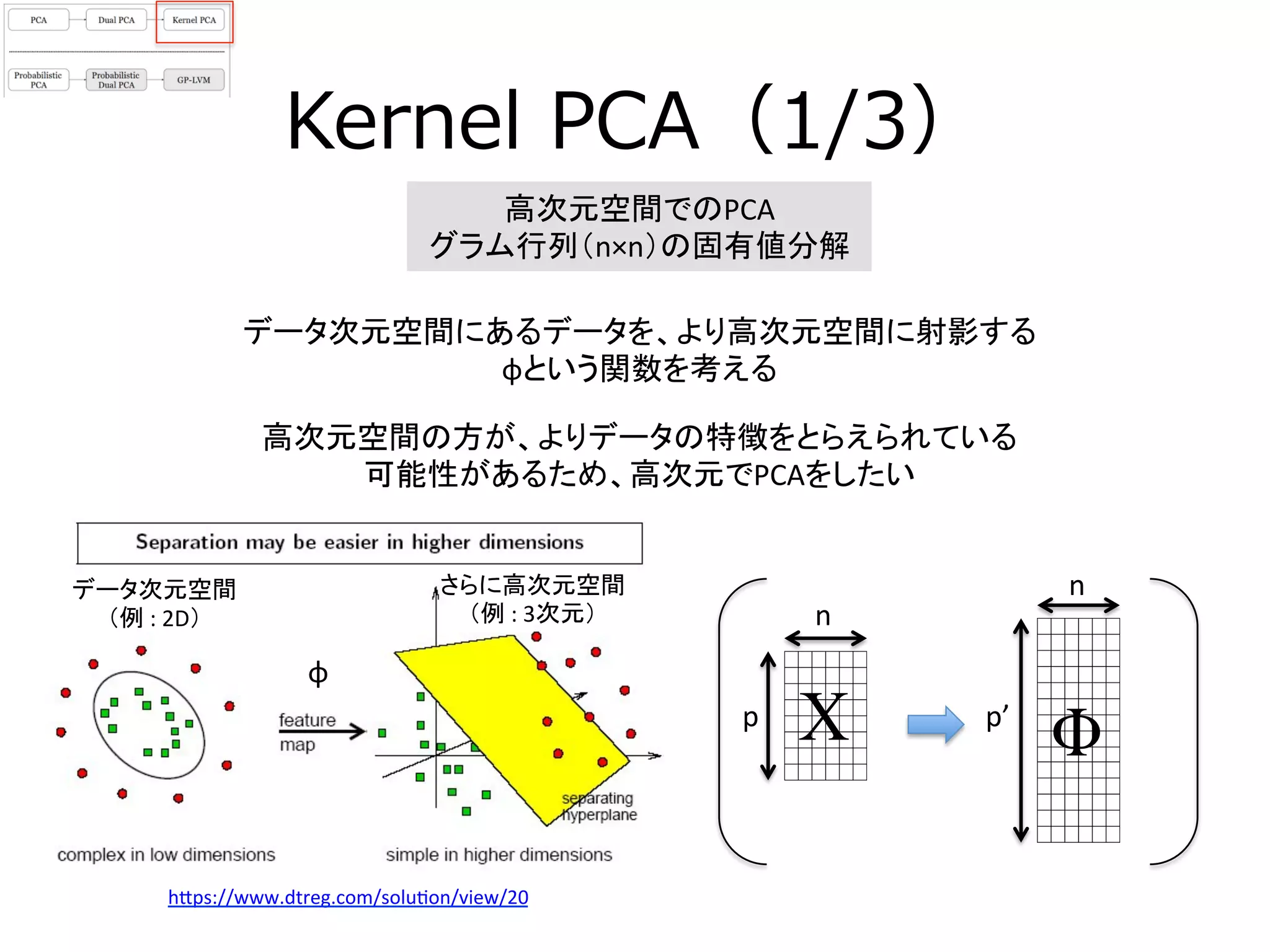
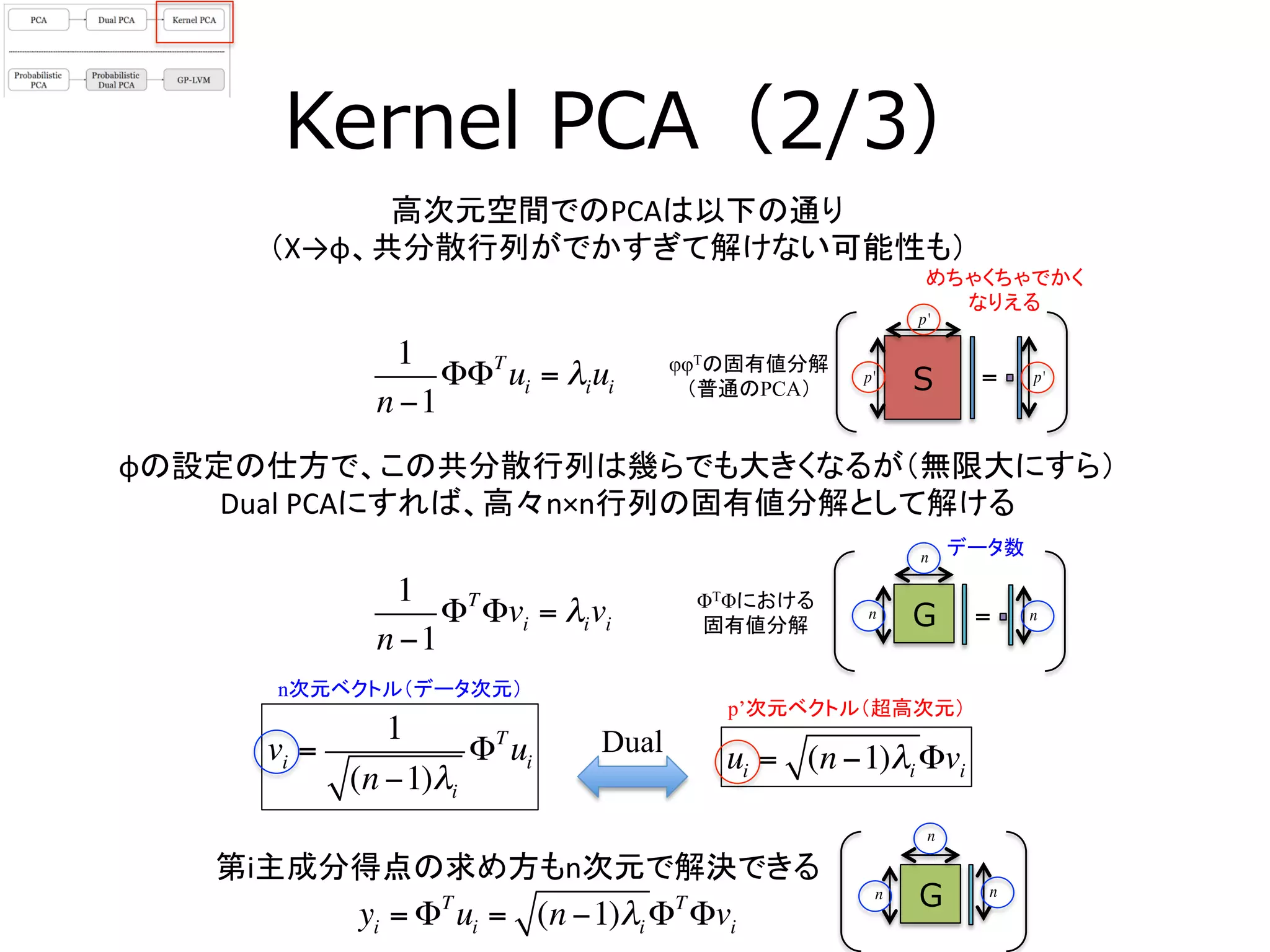
14. 15. Kernel PCA(2/3)
高次元空間でのPCAは以下の通り
(X→φ、共分散行列がでかすぎて解けない可能性も)
1
n −1
ΦΦT
ui = λiui
φφTの固有値分解
(普通のPCA)
ΦTΦにおける
固有値分解
1
n −1
ΦT
Φvi = λivi
S =p' p'
p'
G =n n
n
φの設定の仕方で、この共分散行列は幾らでも大きくなるが(無限大にすら)
Dual
PCAにすれば、高々n×n行列の固有値分解として解ける
めちゃくちゃでかく
なりえる
vi =
1
(n −1)λi
ΦT
ui ui = (n −1)λi Φvi
n次元ベクトル(データ次元)
p’次元ベクトル(超高次元)
yi = ΦT
ui = (n −1)λi ΦT
Φvi
第i主成分得点の求め方もn次元で解決できる
データ数
Gn
n
n
Dual
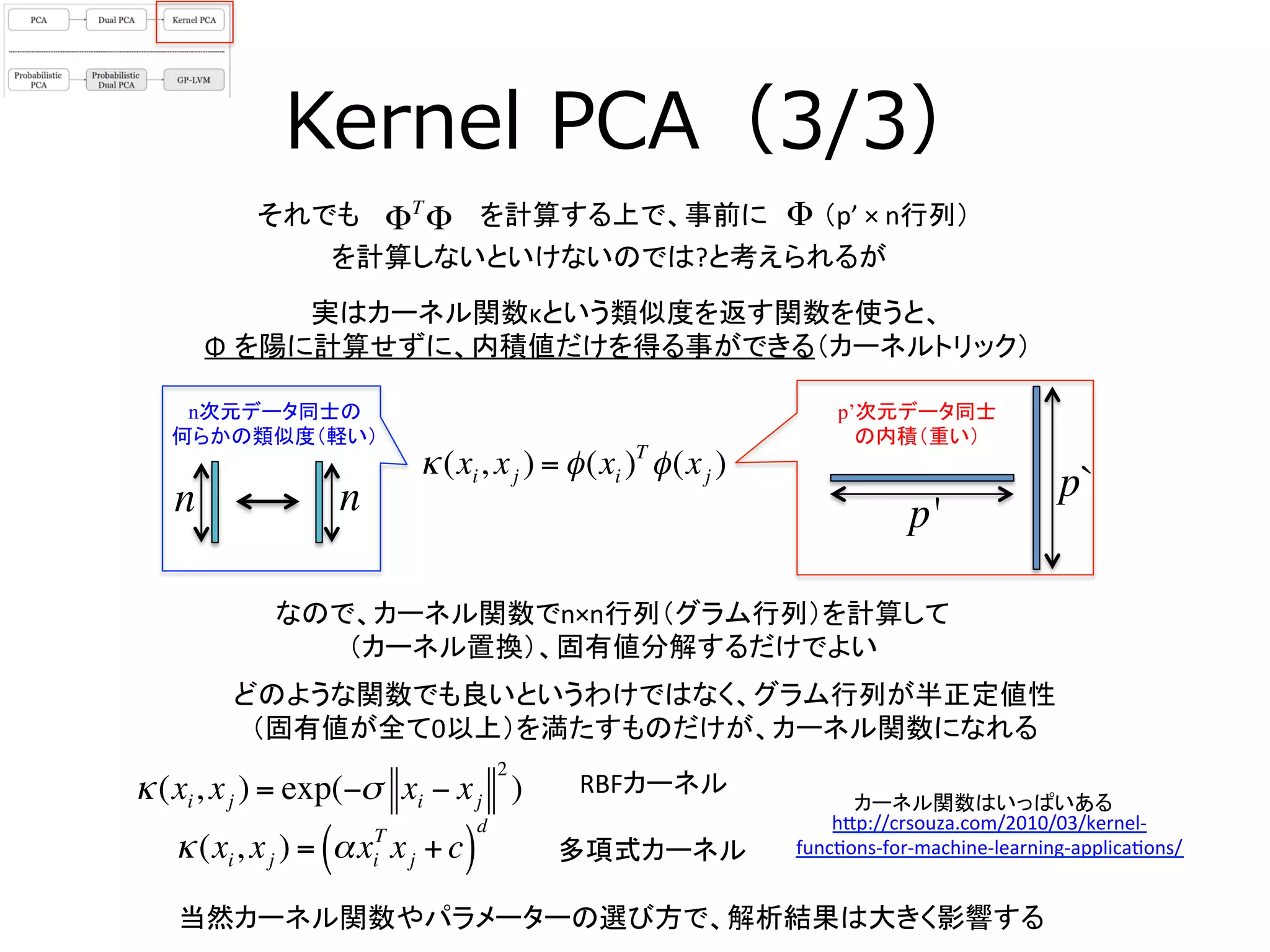
16. Kernel PCA(3/3)
ΦT
Φそれでも
当然カーネル関数やパラメーターの選び方で、解析結果は大きく影響する
実はカーネル関数κという類似度を返す関数を使うと、
Φ を陽に計算せずに、内積値だけを得る事ができる(カーネルトリック)
どのような関数でも良いというわけではなく、グラム行列が半正定値性
(固有値が全て0以上)を満たすものだけが、カーネル関数になれる
を計算する上で、事前に
を計算しないといけないのでは?と考えられるが
Φ
κ(xi, xj ) = φ(xi )T
φ(xj )
n次元データ同士の
何らかの類似度(軽い)
p’次元データ同士
の内積(重い)
nn p'
p`
RBFカーネル
カーネル関数はいっぱいある
κ(xi, xj ) = exp(−σ xi − xj
2
)
κ(xi, xj ) = αxi
T
xj +c( )
d h[p://crsouza.com/2010/03/kernel-‐
func3ons-‐for-‐machine-‐learning-‐applica3ons/
多項式カーネル
(p’
×
n行列)
なので、カーネル関数でn×n行列(グラム行列)を計算して
(カーネル置換)、固有値分解するだけでよい
17. p(xi | yi )
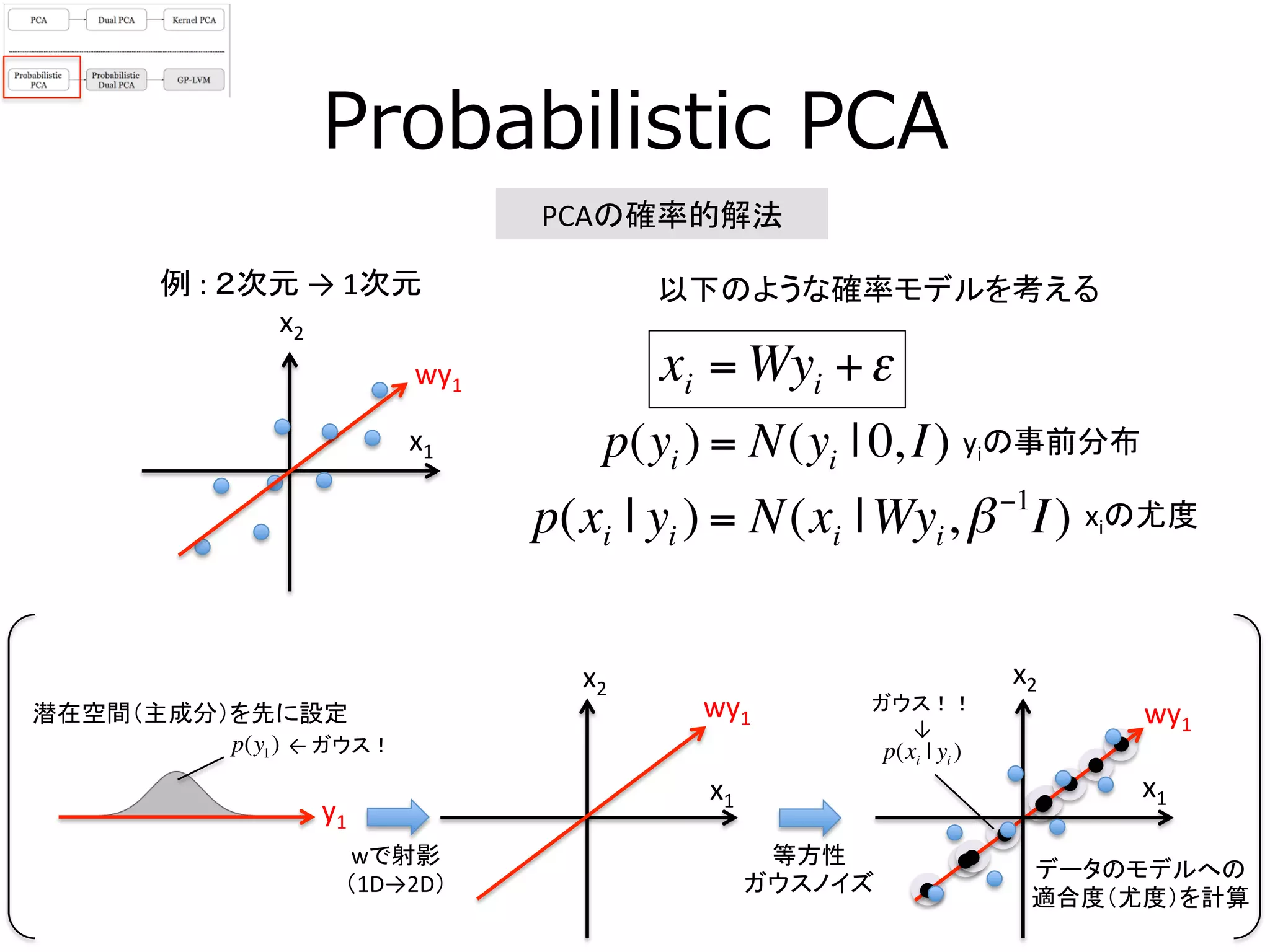
Probabilistic PCA
PCAの確率的解法
xi = Wyi +ε
以下のような確率モデルを考える
x1
x1
x2
x2
wy1
wで射影
(1D→2D)
等方性
ガウスノイズ
p(y1)
y1
潜在空間(主成分)を先に設定
wy1
x1
wy1
データのモデルへの
適合度(尤度)を計算
x2
p(yi ) = N(yi | 0, I)
p(xi | yi ) = N(xi |Wyi,β−1
I)
←
ガウス!
ガウス!!
↓
yiの事前分布
xiの尤度
例
:
2次元
→
1次元
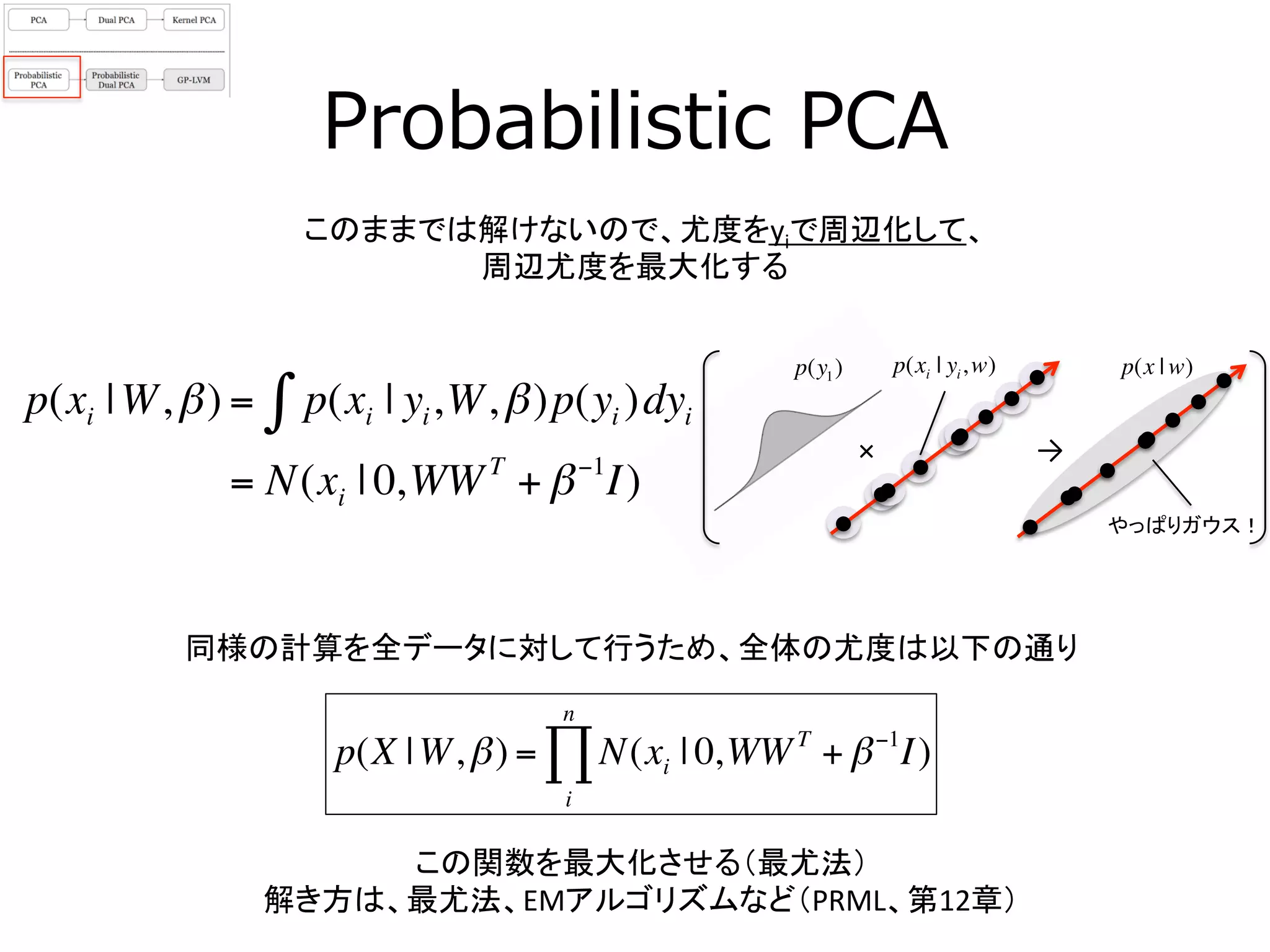
18. 19. 20. Probabilistic Dual PCA
尤度をyではなくWで周辺化したもの
尤度をWで周辺化
p(xi | yi,β) = p(xi | yi,W,β)p(W)dW∫
= N(xi | 0,YT
Y + β−1
I)
同様の計算を全データに対して行うため、全体の尤度は以下の通り
p(X |Y,β) = N(xi;d | 0,YT
Y + β−1
I)
d=1
D
∏
Wの事前分布を設定する(D:
潜在空間の次元数)
p(W) = N(wd | 0, I)
d=1
D
∏
=
やっぱりガウス!!
p(W) p(x | y)p(xi | yi )
尤度と共役関係にある
(式が簡単になる)ガウス分布を設定
=×
p(xi | yi,w)
解析的に解けない
ので、最急勾配法
などで最適化
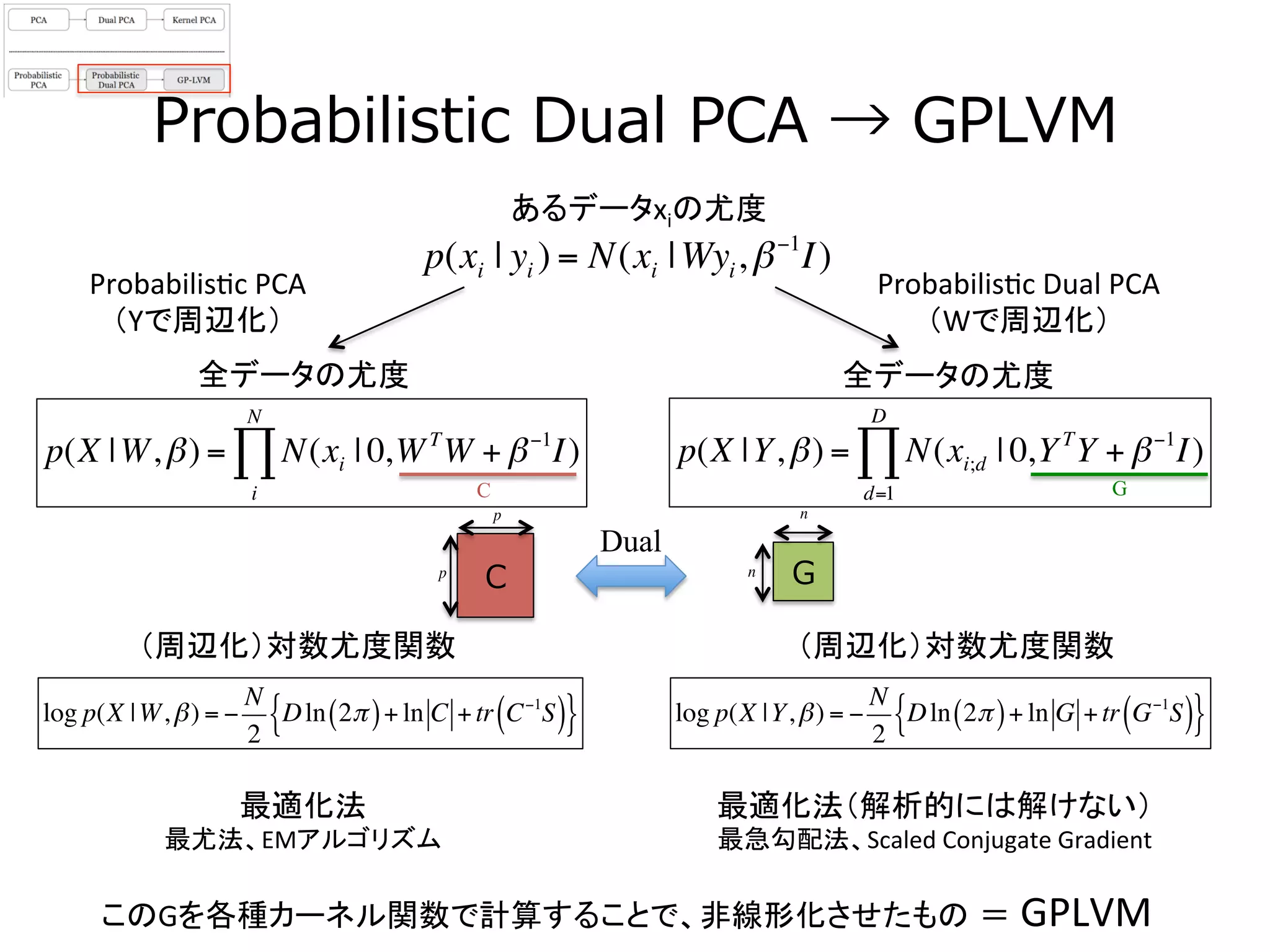
21. Probabilistic Dual PCA → GPLVM
あるデータxiの尤度
p(X |Y,β) = N(xi;d | 0,YT
Y + β−1
I)
d=1
D
∏p(X |W,β) = N(xi | 0,WT
W + β−1
I)
i
N
∏
Probabilis3c
PCA
(Yで周辺化)
Probabilis3c
Dual
PCA
(Wで周辺化)
p(xi | yi ) = N(xi |Wyi,β−1
I)
このGを各種カーネル関数で計算することで、非線形化させたもの = GPLVM
Gn
n
Dual
GC
Cp
p
(周辺化)対数尤度関数
最適化法
最尤法、EMアルゴリズム
最適化法(解析的には解けない)
最急勾配法、Scaled
Conjugate
Gradient
(周辺化)対数尤度関数
全データの尤度
全データの尤度
log p(X |W,β) = −
N
2
Dln 2π( )+ ln C +tr C−1
S( ){ } log p(X |Y,β) = −
N
2
Dln 2π( )+ ln G +tr G−1
S( ){ }
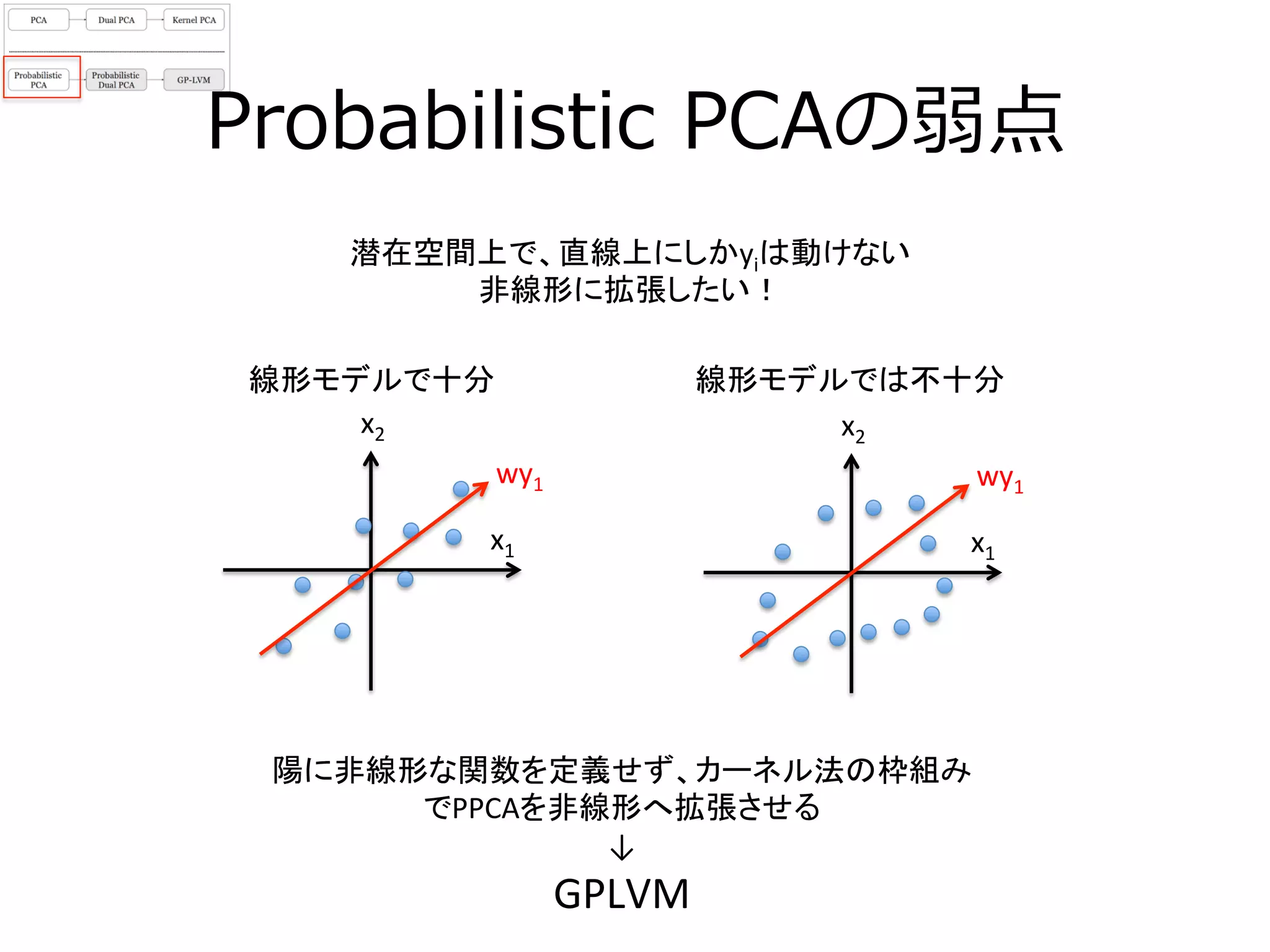
22. 23. GPLVMの拡張モデル
・
Gaussian
Process
Dynamic
Model(GPDM)
:
GPLVMの時系列データへの拡張
h[p://www.dgp.toronto.edu/~jmwang/gpdm/
・
Bayesian
GPLVM
:
GPLVMのベイズ版
→
パラメーターの分布、データの予測分布が手に入る
h[p://inverseprobability.com/vargplvm/
24. GPLVMの拡張モデル
・
Scaled
Gaussian
Process
Latent
Variable
Model
(SGPLVM)
:
正規化をほどこしたGPLVM
h[p://www.cvlibs.net/publica3ons/Geiger2007.pdf
・
Balanced
GPDM
(BGPDM) : 潜在空間でより滑らかにフィッティングするGPDM
比較論文
:
Comparing
GPLVM
Approaches
for
Dimensionality
Reduc3on
in
Character
Anima3on
h[p://www.cs.toronto.edu/~fleet/research/Papers/urtasunCVPR06.pdf
・
Supervised
GPDM
(SGPLVM) : ラベル情報も利用したGPLVM(Jiang,
X
et
al.,
2012)
25. バイオ分野での適⽤用事例例
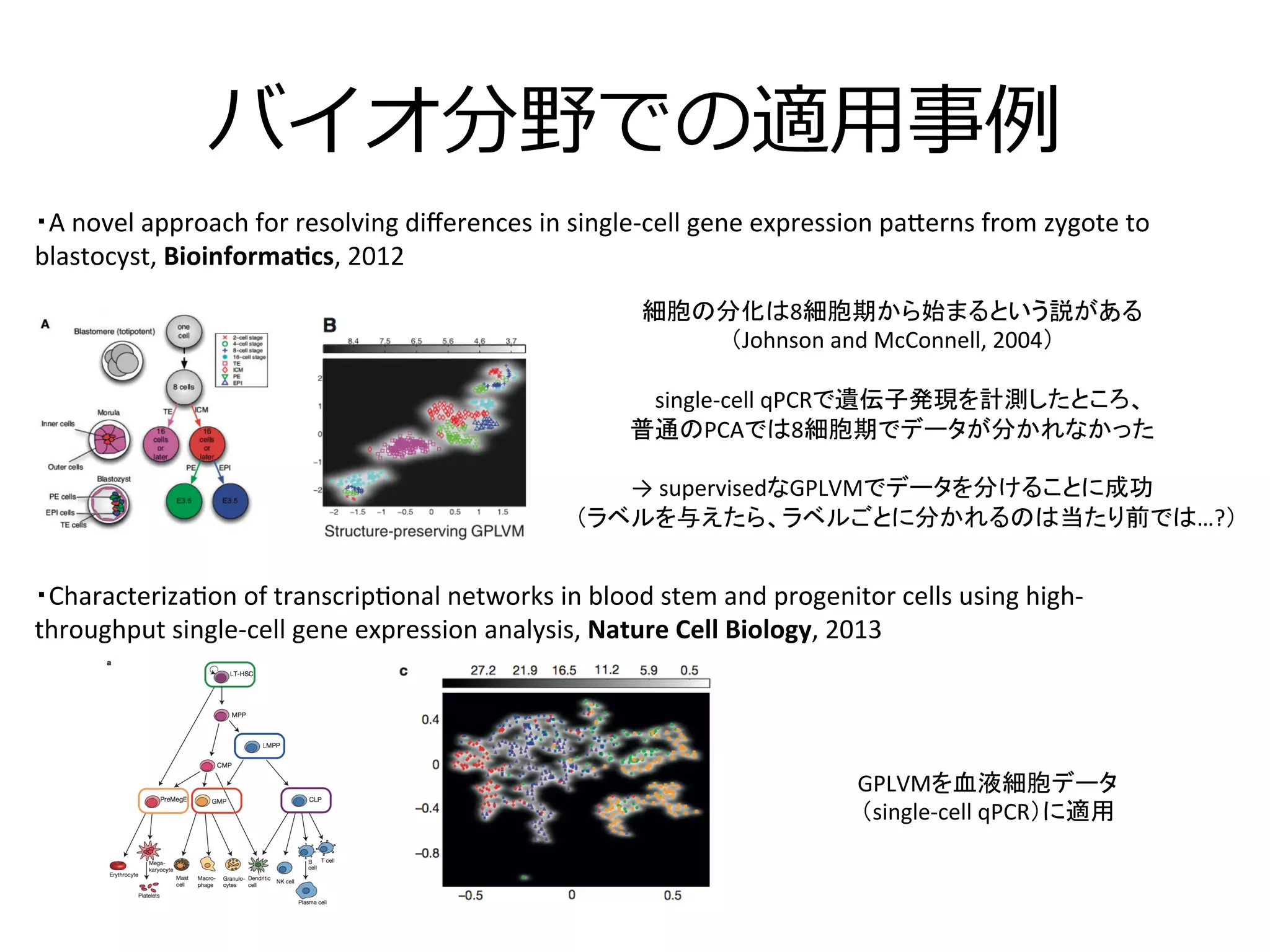
・Characteriza3on
of
transcrip3onal
networks
in
blood
stem
and
progenitor
cells
using
high-‐
throughput
single-‐cell
gene
expression
analysis,
Nature
Cell
Biology,
2013
・A
novel
approach
for
resolving
differences
in
single-‐cell
gene
expression
pa[erns
from
zygote
to
blastocyst,
Bioinforma2cs,
2012
細胞の分化は8細胞期から始まるという説がある
(Johnson
and
McConnell,
2004)
single-‐cell
qPCRで遺伝子発現を計測したところ、
普通のPCAでは8細胞期でデータが分かれなかった
→
supervisedなGPLVMでデータを分けることに成功
(ラベルを与えたら、ラベルごとに分かれるのは当たり前では…?)
GPLVMを血液細胞データ
(single-‐cell
qPCR)に適用
26. バイオ分野での適⽤用事例例
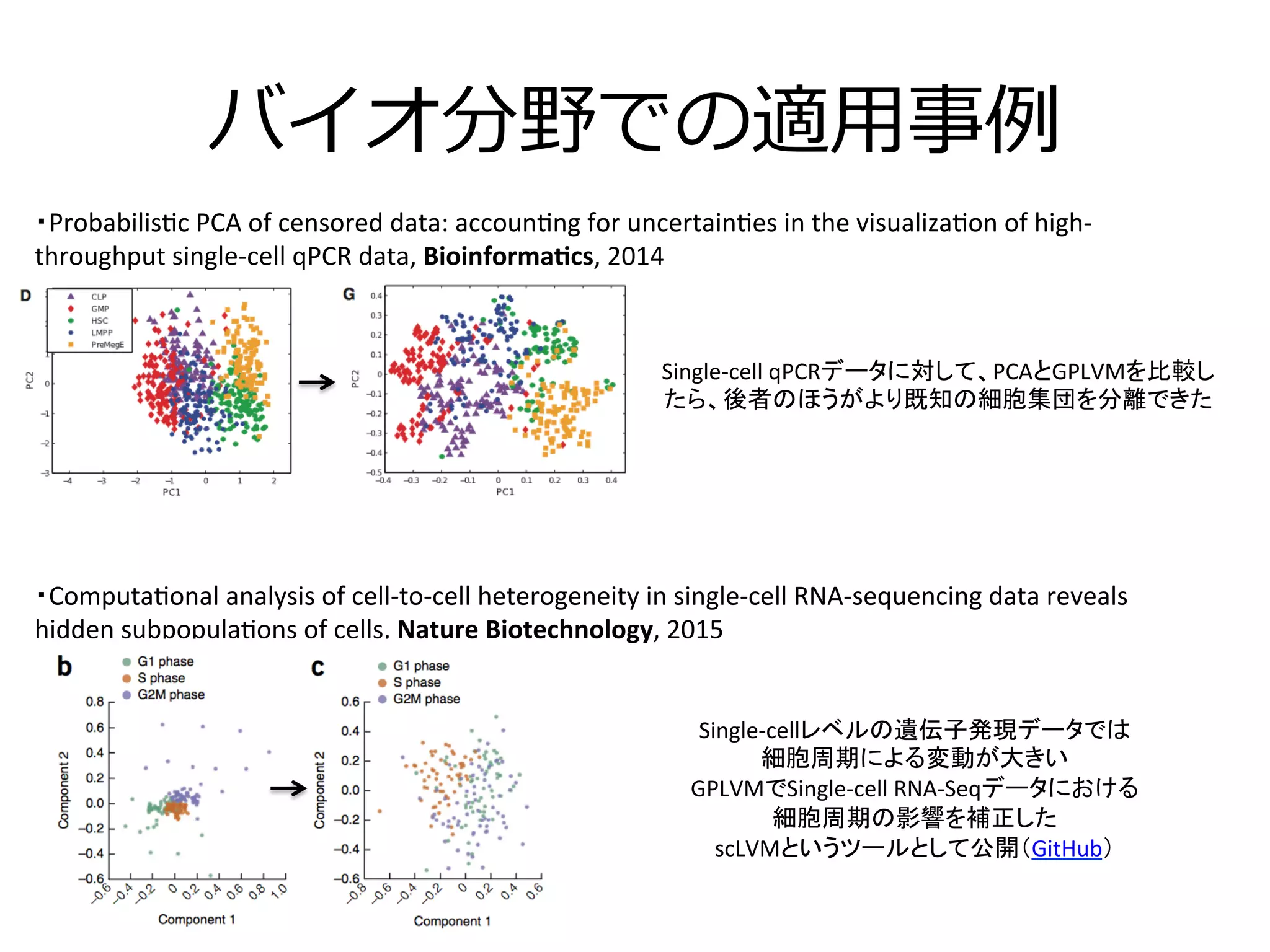
・Computa3onal
analysis
of
cell-‐to-‐cell
heterogeneity
in
single-‐cell
RNA-‐sequencing
data
reveals
hidden
subpopula3ons
of
cells,
Nature
Biotechnology,
2015
・Probabilis3c
PCA
of
censored
data:
accoun3ng
for
uncertain3es
in
the
visualiza3on
of
high-‐
throughput
single-‐cell
qPCR
data,
Bioinforma2cs,
2014
Single-‐cellレベルの遺伝子発現データでは
細胞周期による変動が大きい
GPLVMでSingle-‐cell
RNA-‐Seqデータにおける
細胞周期の影響を補正した
scLVMというツールとして公開(GitHub)
Single-‐cell
qPCRデータに対して、PCAとGPLVMを比較し
たら、後者のほうがより既知の細胞集団を分離できた
27. まとめ
• GPLVM = Probabilistic Kernel PCA
• PCA → 共分散⾏行行列列(XXT)の固有値分解
• Dual PCA → サンプル側での共分散⾏行行列列(XTX)の固有値分解で解いたPCA
– 嬉しいこと : pとnでサイズが⼩小さい⽅方の共分散⾏行行列列で計算すればよい
• Kernel PCA → ⾼高次元空間でのPCA、グラム⾏行行列列の固有値分解
– 嬉しいこと : ⾮非線形への拡張
• Probabilistic PCA → PCAの確率率率的解法
– 嬉しいこと : 予測分布が得られる(ベイズなら)、⽋欠損値を扱える
• GPLVMはKernel PCAとProbabilistic PCAの両⽅方の性質を持つ
• 拡張モデルが幾つも提案されている
• バイオ分野でも多少は使われたことがある

![⾃自⼰己紹介
・露露崎弘毅(つゆざき こうき)
・理理化学研究所 情報基盤センター
バイオインフォマティクス研究開発ユニット
(RIKEN ACCC BiT)
特別研究員
・Single-‐‑‒cell RNA-‐‑‒Seqのデータ解析、解析⼿手法・ソフトウェア
開発をやっています
・連絡先
-‐‑‒ @antiplastics
-‐‑‒ koki.tsuyuzaki [at] gmail.com](https://image.slidesharecdn.com/pcagplvm-151113084515-lva1-app6892/75/PCA-GPLVM-2-2048.jpg)