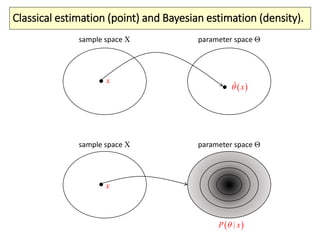
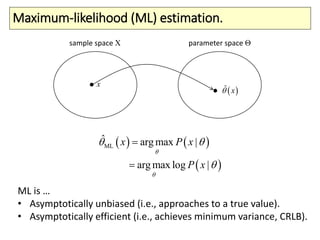
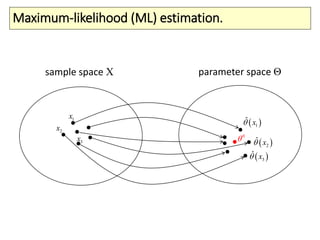
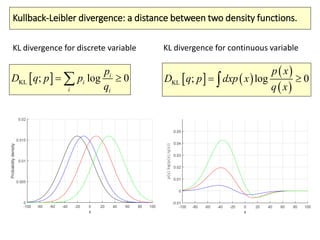
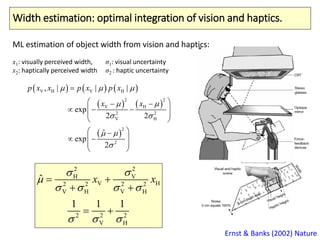
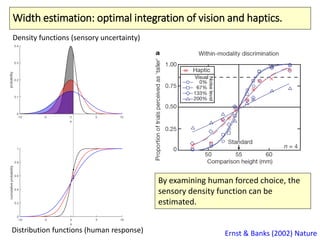
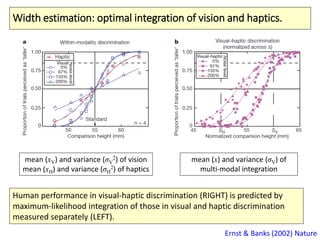
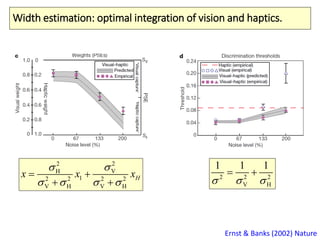
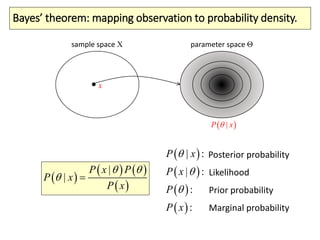
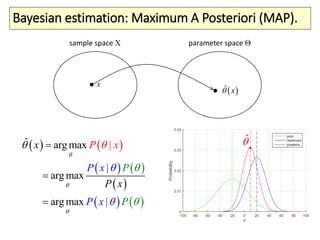
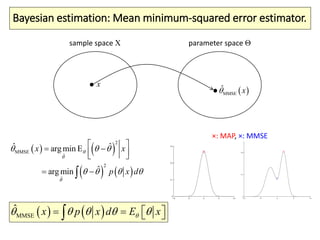
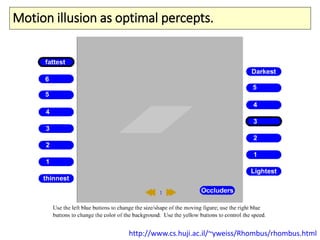
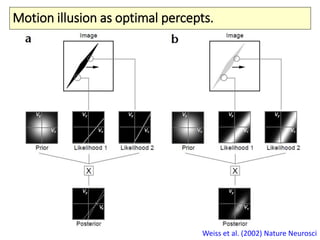
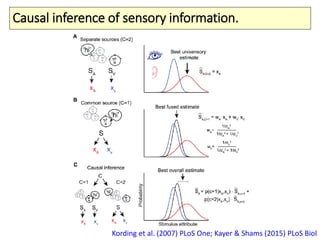
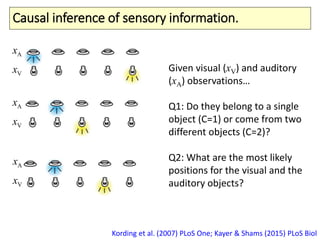
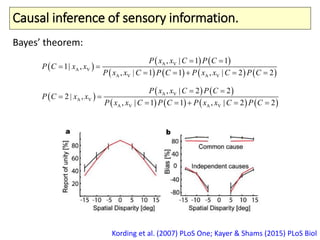
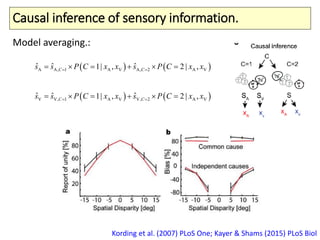
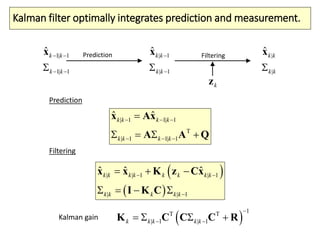
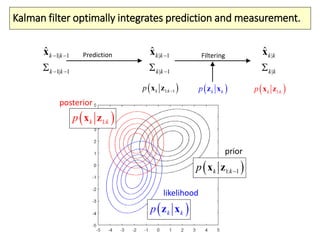
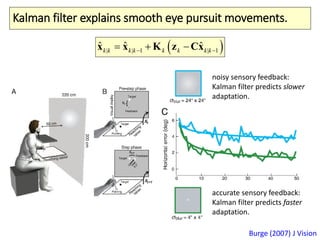
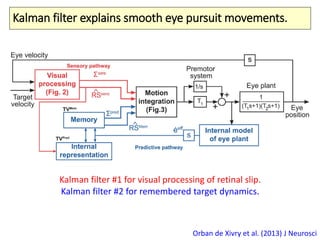
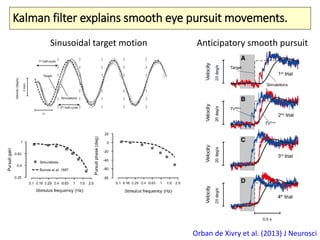
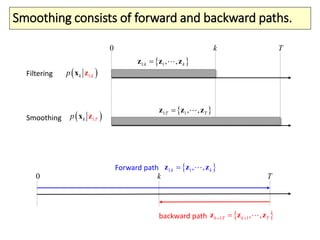
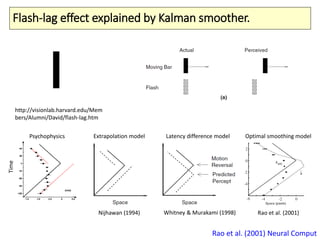
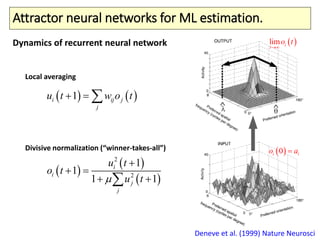
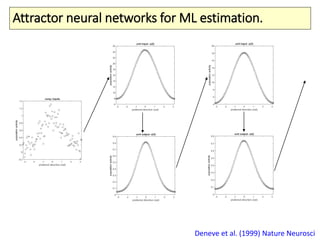
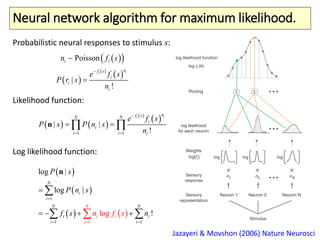
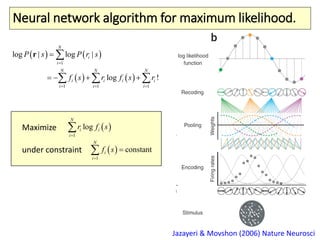
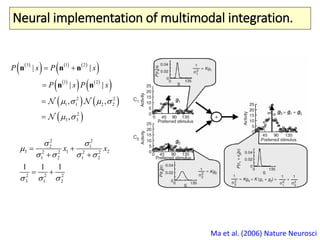
The document covers a summer school lecture on optimal estimation in noisy environments, focusing on techniques such as maximum-likelihood estimation, Bayesian estimation, and Kalman filtering. It discusses key concepts including the Cramer-Rao lower bound, causal inference, and the integration of sensory information from vision and haptics for width estimation. Additionally, the lecture addresses the application of these estimation methods in understanding perception and modeling dynamic systems.

1. Computational Motor
Control Summer School
04: Optimal estimation
in noisy world.
Hirokazu Tanaka
School of Information Science
Japan Institute of Science and Technology

2. In this lecture, we will learn:
• Maximum-likelihood (ML) estimation
• Cramer-Rao’s lower bound
• Bayesian estimation
• Wiener filter
• Kalman filter
• Kalman smoother
• Causal inference
• Information integration
• Postdiction

3. Classical estimation (point) and Bayesian estimation (density).
sample space Χ parameter space Θ
sample space Χ parameter space Θ
 ˆ x
x
x
 |P x

4. Maximum-likelihood (ML) estimation.
sample space Χ parameter space Θ
 ˆ x
x
   
 
ML
ˆ arg max |
arg max log |
x P x
P x




 

ML is …
• Asymptotically unbiased (i.e., approaches to a true value).
• Asymptotically efficient (i.e., achieves minimum variance, CRLB).

5. z
Maximum-likelihood (ML) estimation.
sample space Χ parameter space Θ
 1
ˆ x
1x
2x
 2
ˆ x
 3
ˆ x
3x 0


6. Kullback-Leibler divergence: a distance between two density functions.
 KL ; log 0i
i
i
i
p
D q p p
q
     
 
 KL ; log 0
p x
D q p dxp x
q x
 
KL divergence for discrete variable KL divergence for continuous variable

7. ML as a minimization of KL divergence.
     
 
 
   
KL ; | log
|
=E log E log |
p x
D p x q x dx p x
q x
p x q x



  
      

Minimization of KL divergence
Maximization of
   KL ; |D p x q x   
 E log |q x   
   
1
1
E log | log |
N
i
iq x q x
N
 

   
KL divergence between true density p(x) and parametrized density q(x|θ):
Sampling approximation:

8. ML as a minimization of KL divergence.
         
    
2T
0 0
0
1
T
T
0
1
E log | log loˆ g |ˆ ˆ ˆ ˆ|
ˆ ˆ ˆ
N
i
i
q x q x E q x
N
I
      
 
    

         

 
 


 

 
   
 
2
T T
log | log |
E E
ˆ ˆ
l ˆog |ˆ
q x q x
I q x
 
 
   
 
        

 
  



 0 11ˆ ˆ, I
N
   
 
 
Sampling approximation:
ML is …
• Asymptotically unbiased (i.e., approaches to a true value).
• Asymptotically efficient (i.e., achieves minimum variance, CRLB).
Fisher information:
In the limit of large samples (infinite N), the ML estimator is unbiased and efficient.

9. Cramer-Rao lower bound: scalar parameter case.
Suppose a random variable 𝑋~𝑝(𝑥; 𝜃), where 𝜃 is fixed but
unknown. Assume that 𝑝(𝑥;𝜃) satisfies the “regularity” condition:
where the expectation is with respect to 𝑝(𝑥;𝜃). Then the variance
of any unbiased estimator 𝜃 satisfies
 E log | 0,p x 

 
  


 
1ˆVar
I 
   
 
   
2 2
2
log
E
|
E
| logp x p x
I
 

 
    
     
    
 

 

Fisher information:

10. Cramer-Rao lower bound: vector case.
Suppose a random variable 𝑋~𝑝(𝑥|𝛉), where θ is fixed but
unknown. Assume that 𝑝(𝑥|θ) satisfies the “regularity” condition:
where the expectation is with respect to 𝑝(𝑥;𝜃). Then the variance
of any unbiased estimator 𝛉 satisfies
 E log | 0,p x
 


  
θ
θ
 1ˆCov 
   θ I θ
  
     2
log | log |
E E
log |
ij
i j ji
p x p x p x 
   
   
    

  

        
θ θ
θI
Fisher information matrix:

11. Width estimation: optimal integration of vision and haptics.
22
H
V2 2 2 2
V V
2 2 2
V
V
H
H H
H
1 1 1
ˆ x x


   
  

 
 

Ernst & Banks (2002) Nature
     
   
 
H V
2 2
V
V
V H
2
2
2
H
H
2
, | | |
exp
2 2
exp
2
ˆ
xp x p x p x
x x
  
 
 
 


  
   
 
 
 
  
 
 
ML estimation of object width from vision and haptics:
x1: visually perceived width,
x2: haptically perceived width
σ1: visual uncertainty
σ2 : haptic uncertainty

12. Width estimation: optimal integration of vision and haptics.
Ernst & Banks (2002) Nature
Density functions (sensory uncertainty)
Distribution functions (human response)
By examining human forced choice, the
sensory density function can be
estimated.

13. Width estimation: optimal integration of vision and haptics.
Ernst & Banks (2002) Nature
mean (xV) and variance (σV
2) of vision
mean (xH) and variance (σH
2) of haptics
mean (x) and variance (σV) of
multi-modal integration
Human performance in visual-haptic discrimination (RIGHT) is predicted by
maximum-likelihood integration of those in visual and haptic discrimination
measured separately (LEFT).

14. Width estimation: optimal integration of vision and haptics.
Ernst & Banks (2002) Nature
22
H
1
V
H
2 2 2 2
V V H
Hx x x

   

 

V
2 2 2
H
1 1 1
  
 

15. Bayes’ theorem: mapping observation to probability density.
sample space Χ parameter space Θ
x
 |P x
 
   
 
|
|
P x P
P x
P x
 
 
 
 
 
 
| :
| :
:
:
P x
P x
P
P x



Posterior probability
Likelihood
Prior probability
Marginal probability

16. Bayesian estimation: Maximum A Posteriori (MAP).
sample space Χ parameter space Θ
 ˆ x
x
   
   
 
   
ˆ arg max
arg max
arg m
|
ax
|
|
P x
P x
P
P
P
x
P x
x




 





ˆ

17. Bayesian estimation: Mean minimum-squared error estimator.
sample space Χ parameter space Θ
 MMSE
ˆ x
x
   
   
2
MMSE
ˆ
2
ˆ
ˆ arg min ˆE
arg m ˆin
x x
p x d



 
   
  
  





   MMSE
ˆ x p d Ex x        
×: MAP, ×: MMSE

18. Motion illusion as optimal percepts.
http://www.cs.huji.ac.il/~yweiss/Rhombus/rhombus.html

19. Motion illusion as optimal percepts.
Weiss et al. (2002) Nature Neurosci
        
2
2
, , ,1
, | , exp
2
, , ,
, y
i i i i i i
i i x y x
I x t I xy y y
y
t I x t
P I x
x y t
t v v v v

   
     
 



 
  
   
22 2
2
1
2
, expx y x y
v
P vvv v

 
  
 
          
2
22 2
2 2
, , ,1 1
, | , ex
,
, p
,
2 2
,
y
i i i i i i
x y i i
v i
x y x
y y y
y v
x
I x t I x t I x t
P v v I x t v
y t
v v
 
   
  
  

  
   
   

Prior density: most of objects have small velocity (not moving).
Likelihood: Probability of observed image with given velocity (vx, vy).
   , , , ,x yt y t t t yI x v v I tx     Lucas-Kanade image model:
Posterior density

20. Motion illusion as optimal percepts.
Weiss et al. (2002) Nature Neurosci

21. Causal inference of sensory information.
Kording et al. (2007) PLoS One; Kayer & Shams (2015) PLoS Biol

22. Causal inference of sensory information.
Kording et al. (2007) PLoS One; Kayer & Shams (2015) PLoS Biol
Given visual (xV) and auditory
(xA) observations…
Q1: Do they belong to a single
object (C=1) or come from two
different objects (C=2)?
Q2: What are the most likely
positions for the visual and the
auditory objects?
Ax
Vx
Ax
Vx
Ax
Vx

23. Causal inference of sensory information.
Kording et al. (2007) PLoS One; Kayer & Shams (2015) PLoS Biol
 
   
       
A V
A V
A V A V
,
,
, ,
| 1 1
1|
| 1 1 | 2 2
x
x
x
P x C P C
P C x
P x C P C P x C P Cx
 
 
    
 
   
       
A V
A V
A V A V
,
,
, ,
| 2 2
2 |
| 1 1 | 2 2
x
x
x
P x C P C
P C x
P x C P C P x C P Cx
 
 
    
Bayes’ theorem:

24. Causal inference of sensory information.
Kording et al. (2007) PLoS One; Kayer & Shams (2015) PLoS Biol
   A A, 1 A V A, 2 A V
ˆ ˆ ˆ1| , 2 | ,C Cs s P C x x s P C x x      
   V, 1 A V V, 2V A V
ˆ ˆ ˆ1| , 2 | ,C Cs s P C x x s P C x x      
Model averaging.:

25. Prediction, filtering and smoothing of a dynamic system.
Prediction
Filtering
Smoothing
0 k T
 0 01: 1, ,k kz z z
 1: 1, ,k kz z z
 1: 1, ,T Tz z z
 01:k kp x z
 1:k kp x z
 1:k Tp x z

26. Estimation of dynamic systems: Kalman filter.
1k k k
k k k
  
 
Ax
Cx
w
z v
x
Stochastic state-space model
Problem: Given a sequence of measurements up to step k,
then estimate the conditional mean
and the conditional covariance of the state vector at step k,
 1: 1 2 ,, , , kk z z z z
| 1:
ˆ ,k k k kE   x x z
  | 1 1:
T
: : :
ˆ ˆCov E ,k k k k k k k k k k k
          
x z x x x x z

27. Kalman filter optimally integrates prediction and measurement.
Prediction
| 1
| 1
1| 1
T
1| 1
ˆ ˆ
k k
k
k
k
k
k k
 
 


   
x Ax
A A Q
Filtering
 
 | |
| 1
1
| | 1
ˆ ˆ ˆk k k k k k k k
k k k kk
 

  
   
x x K z Cx
I K C
 
1T T
| 1 | 1k k k k k

    K C C C RKalman gain
1| 1
1| 1
ˆk k
k k
 
 
x | 1
| 1
ˆk k
k k


x |
|
ˆk k
k k
xPrediction Filtering
kz

28. Kalman filter optimally integrates prediction and measurement.
1| 1
1| 1
ˆk k
k k
 
 
x | 1
| 1
ˆk k
k k


x |
|
ˆk k
k k
xPrediction Filtering
 1: 1k kp x z
 k kp z x
 1:k kp x z
 1: 1k kp x z  k kp z x  1:k kp x z
prior
likelihood
posterior

29. Kalman filter: Derivation.
1| 1
1| 1
ˆk k
k k
 
 
x | 1
| 1
ˆk k
k k


x |
|
ˆk k
k k
xPrediction Filtering
kz
     
   
 
1: 1 1 1 1
1 1 1 1| 1 1| 1
| 1
1
|
: 1
1
ˆ; , ; ,
ˆ; ,
kk k k k kk
k k k k k k k k
k k k k k
p d p p
d
   
    
 

 







x z x x x zx
x x Ax Q x x
x x
 1 1| 1 1| 1
ˆ; ,k k k k k    x x  | 1 | 1; ˆ ,k k k k k x x  | |; ,ˆk k k k kx x
Prediction
Filtering
 
   
 
 1: 1
1: | |
1: 1
ˆ; ,
k k k k
k k k k k k k
k k
p p
p
p


 
z x x z
x z x x
z z

30. Kalman filter: Derivation.
1| 1
1| 1
ˆk k
k k
 
 
x | 1
| 1
ˆk k
k k


x |
|
ˆk k
k k
xPrediction Filtering
kz
, ,
     
        
 
 
   y y
x x xy
yx
x
y
μ
y μ
x
  1 1
, 
      y yxx yy xx yyxy xyμ μx y y
  1 1
, 
     x yy xyy xx xxyx yxμ μy x x
Lemma: When a joint density function of two variables x and y are given as
then conditional probability densities are given as follows:

31. Kalman filter explains smooth eye pursuit movements.
Burge (2007) J Vision
 | | 1 | 1
ˆ ˆ ˆk k k k k k k k   x x K z Cx
noisy sensory feedback:
Kalman filter predicts slower
adaptation.
accurate sensory feedback:
Kalman filter predicts faster
adaptation.

32. Kalman filter explains smooth eye pursuit movements.
Orban de Xivry et al. (2013) J Neurosci
Kalman filter #1 for visual processing of retinal slip.
Kalman filter #2 for remembered target dynamics.

33. Kalman filter explains smooth eye pursuit movements.
Sinusoidal target motion Anticipatory smooth pursuit
Orban de Xivry et al. (2013) J Neurosci

34. Smoothing of Dynamic systems: Kalman smoother.Smoothing consists of forward and backward paths.
Filtering
Smoothing
0 k T
 1: 1, ,k kz z z
 1: 1, ,T Tz z z
 1:k kp x z
 1:k Tp x z
0 k T
Forward path  1: 1, ,k kz z z
backward path  1: 1, ,k T k T z z z

35. Kalman smoother algorithm: RTS smoother.
Forward path: Using the standard algorithm of Kalman filter, compute the
predicted mean and covariance,
and the filtered mean and covariance,
 1| 1| , 1,ˆ , 0,k k k k k T   x
 | |
ˆ , .0 ,,k k k k Tk x
Backward path: Then, the smoothed mean and covariance,
are solved backward in time as follows:
 | |
ˆ , .0 ,,k T k T Tk x
 
 
| | 1| 1|
| | 1| 1|
ˆ ˆ ˆ ˆk T k k k k T k k
T
k T k k k k T k k k
 
 
  
    
x x G x x
G G
 
1
| 1|
T
k k k k k

 G Awhere

36. Flash-lag effect explained by Kalman smoother.
http://visionlab.harvard.edu/Mem
bers/Alumni/David/flash-lag.htm
Psychophysics Extrapolation model Latency difference model Optimal smoothing model
Time
Nijhawan (1994) Whitney & Murakami (1998) Rao et al. (2001)
Rao et al. (2001) Neural Comput

37. Attractor neural networks for ML estimation.
   1i ij j
j
u t w o t  
Deneve et al. (1999) Nature Neurosci
 0i io a
 lim i
t
o t

Dynamics of recurrent neural network
 
 
 
2
2
1
1
1 1
i
j
i
j
u t
o t
u t

 
 
Local averaging
Divisive normalization (“winner-takes-all”)

38. Attractor neural networks for ML estimation.
Deneve et al. (1999) Nature Neurosci

39. Neural network algorithm for maximum likelihood.
  Poissoni in f s
 
 
 |
!
ii s
i
i
nf
if
s
e s
P r
n


   
 
 
1 1
|
!
|
ii
nsN fN
i
i
i
ii
f
s n
e s
P P
n
s

 
  n
 
 
   
1
1 11
log
log
|
log
|
!
N
i
N N
i i
N
i ii i
i
i
n
sP
n sP
f nfs s

  

   

  
n
Jazayeri & Movshon (2006) Nature Neurosci
Probabilistic neural responses to stimulus s:
Likelihood function:
Log likelihood function:

40. Neural network algorithm for maximum likelihood.
Jazayeri & Movshon (2006) Nature Neurosci
   
   
1
1 1 1
log log
log
|
!
|
N
i
N N N
i i i
i
i i i i
P P
f s r
r
r
s
f
s
s

  

   

  
r
Maximize  
1
logi i
N
i
r f s


 
1
constant
N
i
if s

under constraint

41. Neural implementation of multimodal integration.
Ma et al. (2006) Nature Neurosci
     
2
2
1 1 0
log | log const. const.
2
N N
i
i i i
i i
n
P s n f s s s
 
      n
   2
| ; ,s sP   n
2
21 0
1 1
,
N
i ii
N N
i ii i
n
n n
s 
 
 


 
If tuning function is Gaussian with mean si and variance σ0
2,
then, the likelihood function is also Gaussian:
where
     
2
2
0 22
00
1
, exp ,
22
i
i if ss
s s



 
  
 
 
Population activity Likelihood Population activity Likelihood

42. Neural implementation of multimodal integration.
Ma et al. (2006) Nature Neurosci
 
     
 
 
   
 
   
 
2
3
3 1 2
1 2
2 2
1 1 2
2
3
| |
, ,
| |
,
s s
s s
P P
P P
   
 




n n n
n n
2 2
2
3 12 2 2 2
1
1
1
2 2 2
1
2
2 2
3 2
1 1 1
x x
 

   
  
 
 
 

43. Summary
• Inference from noisy measurements is formulated as a
statistical inference problem.
• Statistical inference is categorized into classical point
estimation and Bayesian probability estimation.
• Human performance in psychophysical experiments
matches the predictions of optimal estimation.
• The computation of optimal inference can be
implemented by a few neural mechanisms.

44. References
• Ernst, M. O., & Banks, M. S. (2002). Humans integrate visual and haptic information in a statistically optimal
fashion. Nature, 415(6870), 429-433.
• Weiss, Y., Simoncelli, E. P., & Adelson, E. H. (2002). Motion illusions as optimal percepts. Nature neuroscience, 5(6),
598-604.
• Kording, K. P., & Wolpert, D. M. (2004). Bayesian integration in sensorimotor learning. Nature, 427(6971), 244-247.
• Kording, K. P., Beierholm, U., Ma, W. J., Quartz, S., Tenenbaum, J. B., & Shams, L. (2007). Causal inference in
multisensory perception.
• Kayser, C., & Shams, L. (2015). Multisensory causal inference in the brain. PLoS biology, 13(2).
• Burge, J., Ernst, M. O., & Banks, M. S. (2008). The statistical determinants of adaptation rate in human reaching.
Journal of Vision, 8(4), 20.
• de Xivry, J. J. O., Coppe, S., Blohm, G., & Lefevre, P. (2013). Kalman filtering naturally accounts for visually guided
and predictive smooth pursuit dynamics. The Journal of Neuroscience, 33(44), 17301-17313.
• Rao, R. P., Eagleman, D. M., & Sejnowski, T. J. (2001). Optimal smoothing in visual motion perception. Neural
Computation, 13(6), 1243-1253.
• Deneve, S., Latham, P. E., & Pouget, A. (1999). Reading population codes: a neural implementation of ideal
observers. Nature neuroscience, 2(8), 740-745.
• Jazayeri, M., & Movshon, J. A. (2006). Optimal representation of sensory information by neural populations. Nature
neuroscience, 9(5), 690-696.
• Ma, W. J., Beck, J. M., Latham, P. E., & Pouget, A. (2006). Bayesian inference with probabilistic population codes.
Nature neuroscience, 9(11), 1432-1438.

45. Exercise
• Write a Matlab code for Kalman filter and Kalman
smoothing, and examine the difference.
• Psychophysics: Smooth eye pursuit experiment using
GazeParser (http://gazeparser.sourceforge.net/).