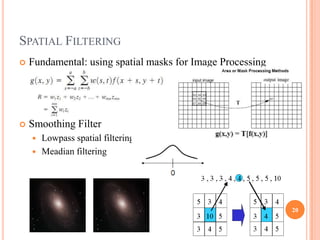
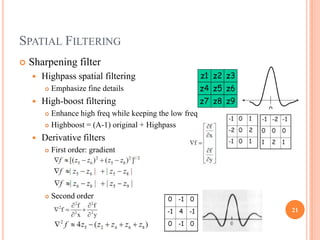
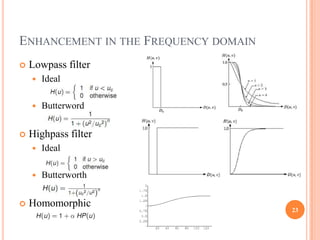
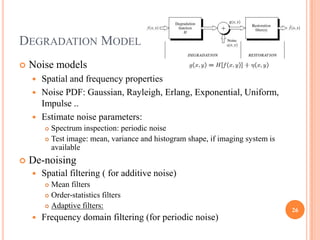
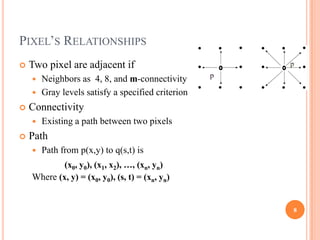
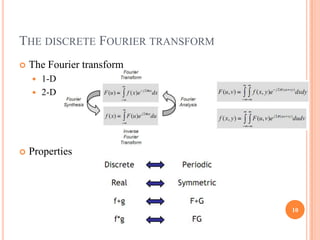
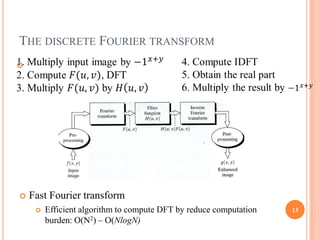
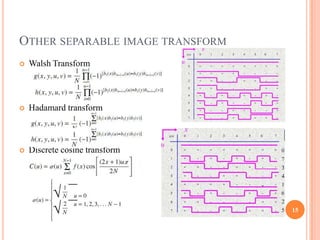
This document provides an overview of digital image processing and is divided into multiple parts. Part I discusses digital image fundamentals, image transforms, image enhancement, image restoration, image compression, and image segmentation. It introduces key concepts such as digital image systems, sampling and quantization, pixel relationships, and image transforms in both the spatial and frequency domains. Image processing techniques like filtering, histogram processing, and frequency domain filtering are also summarized.

1. DIGITAL IMAGE PROCESSING
PART I
1 Thuong Nguyen

2. CONTENT
 Digital image fundamentals
 Image transform
 Image enhancement
 Image restoration
 Image compression
2

3. I. DIGITAL FUNDAMENTAL
 Digital Image Processing System
 Sampling and Quantization
 Relationships between pixels
3

4. DIP SYSTEM
4

5. DIP SYSTEM
5

6. DIP SYSTEM
6

7. SAMPLING AND QUANTIZATION
 Quantization: limit of intensity resolution
 Sampling: Limit of spatial and temp resolution
 Uniform and non-uniform
7

8. PIXEL’S RELATIONSHIPS
 Two pixel are adjacent if
 Neighbors as 4, 8, and m-connectivity
 Gray levels satisfy a specified criterion
 Connectivity
 Existing a path between two pixels
 Path
 Path from p(x,y) to q(s,t) is
(x0, y0), (x1, x2), …, (xn, yn)
Where (x, y) = (x0, y0), (s, t) = (xn, yn)
8

9. II. IMAGE ENHANCEMENT IN FREQ DOMAIN
 Discrete Fourier Transform
 Other Image Transform
 Hotelling Transform
9

10. THE DISCRETE FOURIER TRANSFORM
 The Fourier transform
 1-D
 2-D
 Properties
10

11. THE DISCRETE FOURIER TRANSFORM
 Discrete Fourier transform pair
 One dimensional
 Two dimensional
11

12. THE DISCRETE FOURIER TRANSFORM
 2D FFT and Image Processing
12

13. THE DISCRETE FOURIER TRANSFORM

 Fast Fourier transform
 Efficient algorithm to compute DFT by reduce computation 13
burden: O(N2) – O(NlogN)

14. OTHER SEPARABLE IMAGE TRANSFORM
 General relation ship
 Several condition
 Separable
 Symmetric
 Separable kernel can be compute in two step of 1D transf
 For separable and symmetric kernel
14

15. OTHER SEPARABLE IMAGE TRANSFORM
 Walsh Transform
 Hadamard transform
 Discrete cosine transform
15

16. HOLTELLING TRANSFORM
Mean:
M
1
x1 mx E{x} xk
x2 M k 1
x1 . ,........, x M Covariance:
M
. T 1 T T
xn Cx E{( x mx )( x mx ) } xk xk mk mk
M k 1
M data points
16

17. III. IMAGINE ENHANCEMENT
 Basic intensity functions
 Histogram processing
 Spatial Filtering
 Enhancement in the Frequency domain
 Color image processing
17

18. BASIC INTENSITY FUNCTIONS
 Spatial domain process
 Image negatives:
 intensity level in the range [0, L-1]
 s=L–1–r
 Log trans
 s = c log(1 + r)
 Power law (gramma) trans
 s=cr
 Piecewise-Linear Trans
 Contrast stretching
 Intensity level slicing 18
 Bit plane slicing

19. HISTOGRAM PROCESSING
 Histogram
 Histogram equalization:
 Histogram matching
 Local histogram processing
 Image subtraction
 Image averaging
19

20. SPATIAL FILTERING
 Fundamental: using spatial masks for Image Processing
 Smoothing Filter
 Lowpass spatial filtering
 Meadian filtering
20

21. SPATIAL FILTERING
 Sharpening filter
 Highpass spatial filtering
 Emphasize fine details
 High-boost filtering
 Enhance high freq while keeping the low freq
 Highboost = (A-1) original + Highpass
 Derivative filters
 First order: gradient
 Second order
21

22. ENHANCEMENT IN THE FREQUENCY DOMAIN
Spatial domain Frequency domain
 Definition  Definition
 Chang pixel position  changes  Change in image position 
changes in spatial frequency
in the scene
 Which image intensity values are
 Distance is real
changing in the spatial domain
image
 Processing  Processing
 Directly process the input image  Transform the image to its
pixel array frequency representation
 Perform image processing
 compute
22

23. ENHANCEMENT IN THE FREQUENCY DOMAIN
 Lowpass filter
 Ideal
 Butterword
 Highpass filter
 Ideal
 Butterworth
 Homomorphic
23

24. COLOR IMAGE PROCESSING
 Background
 Human can perceive thousands of colors
 Two major area: full color and pseudo color
 Color quantization: 8-bit or 24bit
 Color fundamental
 Result of light in the rentina: 400-700nm
 Characterization of light: monochromatic and gray level
 Radiance: total amount of energy emitted by light source
 Brightness: intensity
 Luminance: amount of energy perceived by obervers, in lumens
 Color characters
 Hue
 Saturation
 Birghtness 24

25. IV. IMAGE RESTORATION
 Degradation Model
 Diagonalization of Circulant & Block-Circulant Matrices
 Algebraic Approach
 Inverse Filtering
 Weiner Filter
 Constrained LS Restoration
 Interactive Restoration
 Restoration at Spatial Domain
 Geometric transform
25

26. DEGRADATION MODEL
 Noise models
 Spatial and frequency properties
 Noise PDF: Gaussian, Rayleigh, Erlang, Exponential, Uniform,
Impulse ..
 Estimate noise parameters:
 Spectrum inspection: periodic noise
 Test image: mean, variance and histogram shape, if imaging system is
available
 De-noising
 Spatial filtering ( for additive noise)
 Mean filters
 Order-statistics filters
 Adaptive filters:
26
 Frequency domain filtering (for periodic noise)

27. V. IMAGE COMPRESSION
 Fundamentals
 Image Compression Models
 Elements of Information Theory
 Error-Free Compression
 Lossy Compression
 Image Compression standard
27

28. VI. IMAGE SEGMENTATION
 Detection of Discontiuties
 Edge Linking and Boundary Detection
 Thresholding
 Region-Oriented Segmentation
 Motion in Segmentation
28

29. VII. REPRESENTATION AND DESCRIPTION
 Representation Scheme
 Boundary Descriptors
 Regional Descriptors
 Morphology
 Relational Descriptors
29

30. VIII. RECOGNITION AND INTERPRETATION
 Elements of Image Analysis
 Patterns and Pattern Classes
 Decision-Theoretic Methods
 Structural Methods
 Interpretation
30