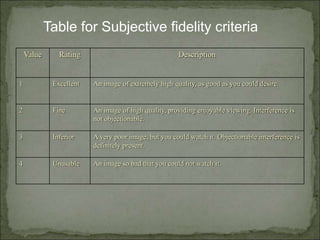
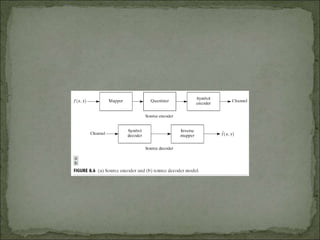
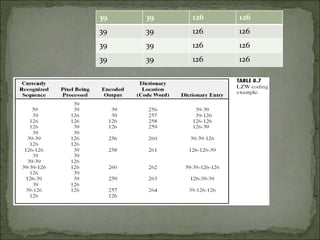
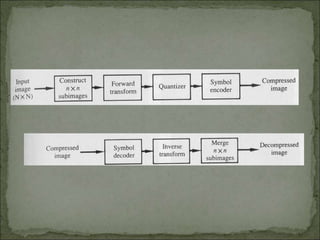
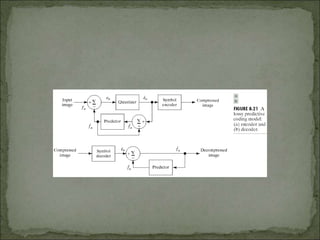
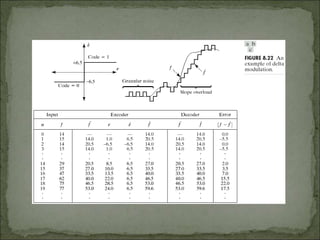
The document discusses various techniques for image compression. It describes how image compression aims to reduce redundant data in images to decrease file size for storage and transmission. It discusses different types of redundancy like coding, inter-pixel, and psychovisual redundancy that compression algorithms target. Common compression techniques described include transform coding, predictive coding, Huffman coding, and Lempel-Ziv-Welch (LZW) coding. Key aspects like compression ratio, mean bit rate, objective and subjective quality metrics are also covered.

1.  The goal of image compression is to reduce the amount of data
required to represent a digital image.
 i.e., remove redundant data
 Image compression is very important for image storage and
image transmission.

2.  Data redundancy is a mathematically quantifiable entity!

3.  Compression ratio:
 Relative data redundancy:



4.  Coding redundancy
 Interpixel redundancy
 Psychovisual redundancy
 The role of compression is to reduce one or more of these
redundancy types.

5. A compression ratio of 10 (10:1) means that the first data set has
10 information carrying units (say, bits) for every 1 unit in the
second (compressed) data set.

6.  Data compression can be achieved by encoding the data using
an appropriate encoding scheme.
 Elements of an encoding scheme:
 Code: a list of symbols (letters, numbers, bits etc.)
 Code word: a sequence of symbols used to represent a piece
of information or an event (e.g., gray levels)
 Word length: number of symbols in each code word

7.  To avoid coding redundancy, codes should be selected
according to the probabilities of the events.
 Idea: Variable Length Coding
 Assign fewer symbols (bits) to the more probable events
(i.e., gray levels in our case)

8.  Focus on gray value images
 Histogram shows the frequency of occurrence of a particular gray
level
 Normalize the histogram and convert to a pdf representation – let rk
be the random variable
pr(rk) = nk/n ;
k = 0, 1,2 …., L-1, where L is the number of gray level values.
Nk is the no. of times that kth gray level appears in the image.
N= total no. of pixels in the image.
l(rk) = number of bits to represent rk
Lavg = k=0 to L-1 l(rk) pr(rk) = average number of bits to encode
one pixel.

9.  the histogram calculations
 where p(rk) is the probability of a pixel to have a
certain value rk
If the number of bits used to represent rk is l(rk), then
)()((
)(
)(
1
0





L
k
kkav
kk
k
rprlL
n
n
n
rh
rp

12.  When the value of pixel can be obtained from its neighboring
pixel, then the redundancy is called interpixel redundancy.
Much of the visual contribution of a single pixel to an image is
redundant, it could have been guessed on the basis of its
neighbors.
 In order to reduce redundancy in 2D arrays
 We can convert them into more efficient, “non-visual” format
 Transformations of this type are called “mappings”
 They are called reversible mappings if the original image
elements can be reconstructed from the transformed data sets.

13.  EG: We can represent the value of pixels in the
“difference” form. The magnitude of difference of two
adjacent pixel is likely to be very small data to represent
the difference.
100 102 140 100
80 90 102 104
85 100 103 102
100 104 103 102
100 2 40 0
80 10 22 24
85 15 18 17
100 4 3 2

14.  Def. of Psychovisual redundancy—certain information has less
importance than other information in normal visual processing
 Human perception of the information in an image does not
involve quantitative analysis of every pixel value (the reason of
existing Psychovisual-Redundancy)
 It is associated with real or quantifiable visual information
 It can be eliminated only because the information itself is not
essential in formal visual processing
 The elimination results in a loss of quantitative information:
quantization

15.  Removal of psycho visually redundant data results in a loss of
real or quantitative visual information.
 Because information of interest may be lost, a repeatable or
reproducible means of quantifying the nature and extent of
information loss is highly desirable.
 Two general classes of criteria are used as the basis for such an
assessment:
1.Objective fidelity criteria
2.Subjective fidelity criteria

16.  When the level of information loss can be expressed as a
function of the original or input image and the compressed and
subsequently decompressed output image, it is said to be based
on an objective fidelity criterion.
 A good example is the root-mean-square (rms) error between
an input and output image.
 Let f(x,y) represents an input image and fˆ(x,y) denote an
estimate or approximation of f(x,y) that results from
compressing and subsequently decompressing the input. For
any value of x and y, the error e(x,y) between f(x,y) and fˆ(x,y)
can be defined as
e(x,y) = fˆ(x,y) –f(x,y)

17. so that the total error between the two images is:
∑∑[ fˆ(x,y) – f(x,y)]
x= 0 to M-1
y= 0 to N-1
Where the images are of size M*N.
 Root mean square error (rms)

18.  By measuring image quality by the subjective evaluations of a
human observer often is more appropriate.
 The evaluations may be made using an absolute rating scale or
by means of side-by-side comparisons of f(x,y) and fˆ(x,y) side
by side comparisons can be done with a scale such as { -3, -2, -
1 0,1,2,3} to represent the subjective evaluations {much worse,
worse, slightly worse, the same, slightly better, better, much
better}, respectively.
 The evaluations are said to be based on subjective fidelity
criteria.

19. Value Rating Description
1 Excellent An image of extremely high quality, as good as you could desire.
2 Fine An image of high quality, providing enjoyable viewing. Interference is
not objectionable.
3 Inferior A very poor image, but you could watch it. Objectionable interference is
definitely present.
4 Unusable An image so bad that you could not watch it.
Table for Subjective fidelity criteria

20.  A compression system consists of two structural blocks: an
encoder and a decoder. An input image f(x,y) is fed into the
encoder which creates a set of symbols from the input data.
After transmission over channel, the encoded representation is
fed to the decoder, where reconstructed output image fˆ(x,y) is
generated.
In general, fˆ(x,y) may or may not be an exact replica of f(x,y).

21.  Previous figure consists of two relatively independent
functions or sub blocks i.e encoder and decoder.
 Source and channel encoder: encoder is made up of
source encoder which removes input redundancies and
channel encoder which increases the noise
immunity(independent) of the source encoder’ output.
 Source and channel decoder: The decoder includes
channel decoder followed by a source decoder. If the
channel between encoder and decoder is noise free, then
channel encoder and decoder are ommitted.

22.  Source encoder: It is responsible to reduce or eliminate
any coding, inter-pixel or psycho visual redundancies in the
input image.
 The corresponding source encoder- mapper, quantizer and
symbol encoder
 Mapper
 transforms the input data into a format designed to reduce
inter-pixel redundancies
 Reversible process
 may and may not directly reduce the amount of data
required to represent the image

23.  Quantizer
 Reduce the accuracy of the mapper’s output in accordance
with some pre-established fidelity criterion
 Reduce psycho-visual redundancy
 Irreversible operation when error compression is omitted
 The symbol encoder
 Creates a fixed or variable-length to represent quantizer
output and maps the output in accordance with the code
 A variable length code is used to represent the mapped and
quantized data set
 Reduce coding redundancy (assign the shortest code words
to the most frequently occurring values
 Source decoder contains only two components: a symbol
decoder and inverse mapper because of irreversible operation
of quantizer

25.  Play an important role when the channel is noisy or prone
to error
 It Was Designed to reduce the impact of channel noise by
inserting a “controlled form of redundancy” into the
source encoded data
 Hamming code
 Append enough bits to the data being encoded that some
minimum number of bits must change between valid code
words
 The 7-bit Hamming (7,4) code h1 h2 h3… h7 is associated
with a 4-bit binary number b3 b2 b1b0
 H1, h2, h4 are even parity check

26. •We will discuss two different
techniques:
- Huffman encoding
- Variable length coding

27.  The most popular approach for removing coding redundancy
 Yields the smallest possible number of code symbols per
source symbol
 Procedures:
(1) create a series of source reduction: combine the two
lowest probability symbol into a single symbol; repeated until
a reduced source with two symbols is reached
(2) code each reduced symbol: start with the smallest source
and working back to the original source;

29. Assign code symbols going backwards

30.  What is Lavg using Huffman coding?
 What is Lavg assuming binary codes?

31.  Advantages:
Huffman coding minimizes coding redundancy. It creates the
optimal code for a set of symbols and probabilities .
Disadvantage:
We need the knowledge of the probabilities of the symbols in
advance.

32.  Assign fixed-length code words to variable length sequence
of source symbols
 Requires no a priori knowledge of the probabilities of
occurrence of the symbol to be coded.
 LZW Coding process
 Construct a “dictionary” containing the source symbols
 Examine the image’s pixel
 The gray sequences that are not in the dictionary are
placed in algorithmically determined locations
 Unique feature: coding dictionary or code book is created
while the data are being encoded

33. 39 39 126 126
39 39 126 126
39 39 126 126
39 39 126 126

34.  Techniques of lossy compression:
 Transform coding
 Lossy predictive coding

35.  based on modifying the transform of an image (such
as Fourier transform-map the image into a set of
transform coefficients)
 a significant number of the coefficients have small
magnitudes and can be quantized
 A transform coding system: encoder and decoder

37.  In the transform code, we use a transform which is
reversible.under this we have transforms such as Fourier
transform, direct cosine transform, walsh hadamard
transform and wavelet based transform.The following
steps are involved in the transform coding:
 Image decomposition
 Transformation
 Quantization
 coding

38.  Image decompsition:An M*N image is split into n*n
sized blocks.This is done to accelerate the speed of
computation during transformation.It will be (M/n)*(N/n)
blocks.
 For eg:an image of the size 256*256 is split into
(256/8)*(256/8)=1024 blocks.
 Transformation:The goal of transformation is to
decorrelate the pixels of each subimage and to contain as
much information as possible into the smallest no. of
transform coefficients.

39.  Quantization: The quantization stage selectively
eliminates or quantizes the coefficients that carry small
information.
 Coding:the coding process codes the coefficients to
further reduce the information to be stored.
It is the quantization stage at which the maximum amount of
compression is achieved.The coding process also helps in
increasing the compression ratio.

40.  Compromise between distortion and compression
ratio
 Adds a quantizer, which absorbs the nearest integer of
the error-free encoder
 The error-free encode must be altered so that the
predictions generated by encode and decoder are
equivalent