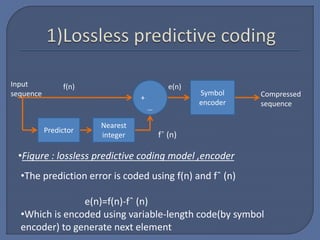
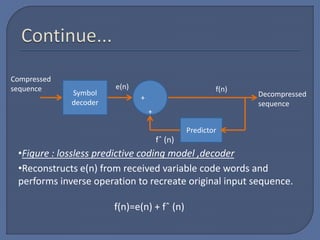
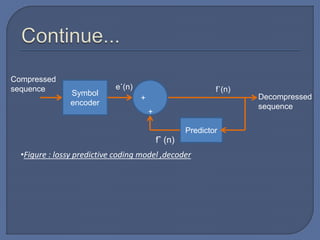
This document discusses predictive coding, which achieves data compression by predicting pixel values and encoding only prediction errors. It describes lossless predictive coding, which exactly reconstructs data, and lossy predictive coding, which introduces errors. Lossy predictive coding inserts quantization after prediction error calculation, mapping errors to a limited range to control compression and distortion. Common predictive coding techniques include linear prediction of pixels from neighboring values and delta modulation.

1. By-Er Payal Suthar
ME(MSU)

2. It is a approach that achieves good
compression without significant overload.
It is Based on eliminating the inter pixel
redundancies of closely spaced pixels by
extracting and coding only the new
information in each pixel.
The new information of a pixel is defined as
the difference between the actual and
predicted value of that pixel.

3. Two types are there,
 1) loss less
 2)lossy

4. +
Symbol
encoder
Predictor
Nearest
integer
e(n)f(n)Input
sequence
fˆ (n)
Compressed
sequence
•Figure : lossless predictive coding model ,encoder
•The prediction error is coded using f(n) and fˆ (n)
e(n)=f(n)-fˆ (n)
•Which is encoded using variable-length code(by symbol
encoder) to generate next element

5. +
Symbol
decoder
Predictor
e(n) f(n)
fˆ (n)
Compressed
sequence
Decompressed
sequence
+
•Figure : lossless predictive coding model ,decoder
•Reconstructs e(n) from received variable code words and
performs inverse operation to recreate original input sequence.
f(n)=e(n) + fˆ (n)

6. Prediction is usually formed by a linear
combination of m previous pixels.
1
m
i n in
i
f round f



 
  
 

•m-is the order of linear predictor,
•round is function used to denote the rounding to nearest
integer operation.
•αi for i = 1,2… m are prediction coefficients.

7.  1-D linear predictive coding : the m samples use to predict
value of each pixel come from current scan line.
 2-D linear predictive coding : the m samples use to predict
value of each pixel come from current and previous scan line.
 3-D linear predictive coding : the m samples use to predict
value of each pixel come from current and previous image
from sequence of images.
 For 1-D,
1
( , ) ( , )
m
in
i
f x y round f x y i


 
  
 


8. Compression achieved is directly related to the
entropy reduction that mapped in to a
prediction error sequence called a prediction
residual.

9. +
Symbol
encoder
Predictor
Quantizer
e˙(n)
f˙(n)
Input
sequence
fˆ (n)
Compressed
sequence
+
+
•Figure : lossy predictive coding model ,encoder
f(n)
e(n)
•Quantizer, which replaces the nearest-integer function of the error-free
encoder, is inserted between the symbol encoder and the point at which the
prediction error is formed.

10. +
Symbol
encoder
Predictor
e˙(n)
Decompressed
sequence
f˙(n)
fˆ (n)
Compressed
sequence
+
•Figure : lossy predictive coding model ,decoder

11. It maps prediction error into a limited range of
outputs, e˙(n) which establishes the amount of
compression and distortion associated with
lossy predictive coding.
Here,
f˙(n)=e˙(n) + fˆ (n)

12. Example: Delta Modulation
in which, fˆ (n)= α f˙(n-1)
and e˙(n)={ +ζ for e(n)>0
- ζ o.w
α= prediction coefficient
ζ= positive constant