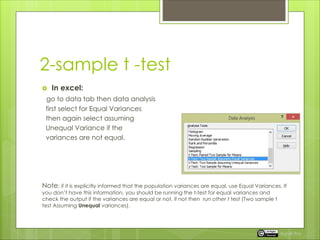
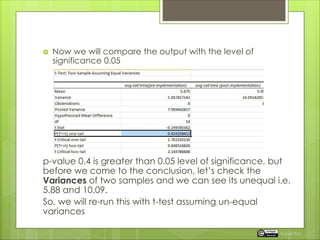
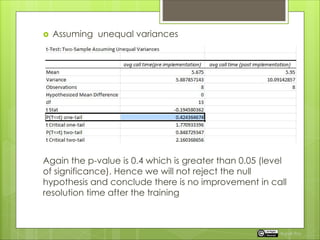
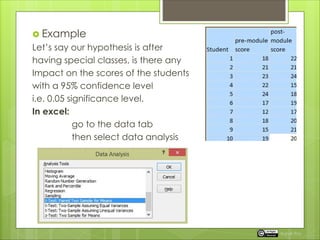
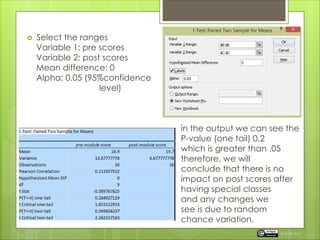
The document explains hypothesis testing, distinguishing between one-tailed (directional) and two-tailed (non-directional) tests, and illustrates their application through examples. It also covers the two-sample t-test and paired t-test for comparing means, explaining how to conduct these tests using Excel and R. Lastly, it highlights the importance of understanding the null and alternative hypotheses and briefly mentions statistical methods like ANOVA for comparing multiple samples.

1. Hypothesis
Testing - II

2. Directional Hypothesis:
 One-Tailed test: A one-tailed test, also
known as a directional hypothesis, is a test
of significance to determine if there is a
relationship between the variables in one
direction.
Rupak Roy

3. Non-Directional Hypothesis Test
 Two – tailed test: A two-tailed test also known as
a non-directional hypothesis is the standard test of
significance to determine if there is a relationship
between variables in
either directions.
A Two-tailed test does this by
dividing the significance level
alpha(a) .05 in two halves
on each side of the
bell curve.
Rupak Roy

4.  In terms of non-directional hypothesis test, we
have to divide the alpha (level of significance)
by 2. Before the level of significance was 5%,
now it will be 0.25 as also shown in the diagram
above.
Non-Directional Hypothesis Test
Rupak Roy

5. Two tailed test is more stricter because we
need more level of confidence to reject the
null hypothesis as compare to one tail test.
Let’s, use some examples to understand one
tail and two tail tests.
Rupak Roy

6. Assume:
Null Hypothesis (Ho): no difference in mileage if we
replace the battery of the car.
Alternative Hypothesis (Ha): difference in mileage if we
replace the battery of the car
If we don’t have a strong believe that there will be a
difference in mileage if we replace the battery of the
car then we should use a two tail test.
Or
if we have a strong believe that the car will give a
better mileage then we will use one tail test.
Rupak Roy

7. Example
 A manufacturing plant have to produce exactly 1000
units of product each day.
Now if we want to check if the manufacturing plant is
able to produce exactly 1000 units per day or different
(more or less)?
Ha: Alternative Hypothesis: Plant producing different
from 1000 units. It can be more or less per day.
In this example in our alternative hypothesis we are not
sure if they can produce more or less per day.
Therefore we will use a two – tail test.
Rupak Roy

8. More simplified
Case1:
Ho: Null Hypothesis: Plant is not producing exactly 1000 units or different.
Ha: Alternative Hypothesis: Plant Producing exactly 1000 units or different
(higher/lower).
i.e. Plant Producing = 1000 units
Plant Producing ≠ 1000 units ( it can be higher or lower)
Case 2:
Ho: Null Hypothesis: plant not producing more than 1000 units.
Ha: Alternative Hypothesis: plant producing more than 1000 units
i.e. Plant producing > 1000 units.
 If you compare Case 1 & 2 we will find in Case 2 we have a strong believe that
the plant is producing more than 1000 units so we will use one tail test
(Directional Hypothesis) as it depicts one direction > or < (greater or smaller
than).
 For Case 1 we don’t have a strong believe that the plant is producing 1000
units or more/less, therefore we will use two-tail test (non-directional
hypothesis)
Rupak Roy

9. 2 sample t-test
 The two sample t-test is used to determine if
the two population means/averages are equal.
A common application is to test if a new
process/event is better to the current
process/event.
Example : Let’s say, the Dell call center wants to
reduce its call resolution time after a special training to
the employees. They want to see if the training really
helped or not to
reduce the call
resolution time,
so they have recorded
the average call time
before and average
call time post.
Rupak Roy

10. 2-sample t -test
 In excel:
go to data tab then data analysis
first select for Equal Variances
then again select assuming
Unequal Variance if the
variances are not equal.
Note: if it is explicitly informed that the population variances are equal, use Equal Variances. If
you don’t have this information, you should be running the t-test for equal variances and
check the output if the variances are equal or not, if not then run other t test (Two sample t
test Assuming Unequal variances).
Rupak Roy

11. Variable 1: sample 1
Variable 2: sample 2
Labels: if column name is present in
the sample range
Alpha: 0.05
Hypothesis Mean Difference: 0
There is no difference between the average call time post
implementation. So the difference we are testing actually a difference
of 0 between sample 1 & sample 2.
So, normally null hypothesis is a set as “no difference between sample
means or m2-m1=0”, but we could have over null hypothesis as the
means differ by fixed value say 6. Than our alternative hypothesis will be
that the mean do not differ by 6 units, in such case our hypothesized
mean difference will be 6.
For example if our null hypothesis value is 6 than hypothesis mean
difference value = 6.
* If Null Hypothesis: value is 0 (remember in 2 Sample t-test we
are testing the means of two population and not one )
than the value of Hypothesis Mean Difference = 0
Rupak Roy

12.  Now we will compare the output with the level of
significance 0.05
p-value 0.4 is greater than 0.05 level of significance, but
before we come to the conclusion, let’s check the
Variances of two samples and we can see its unequal i.e.
5.88 and 10.09.
So, we will re-run this with t-test assuming un-equal
variances
Rupak Roy

13.  Assuming unequal variances
Again the p-value is 0.4 which is greater than 0.05 (level
of significance). Hence we will not reject the null
hypothesis and conclude there is no improvement in call
resolution time after the training
Rupak Roy

14. Paired difference T-tests
 The paired t – test calculates the difference
within each before and after pair of
measurements, determines the mean of these
changes and reports whether this mean of the
differences is statistically significant or not.
 Or in simple words we can say a paired t-test is
used to compare two population means where
we have two pair of observations with after
and before samples and identifies the
observations are statistically significant or not.
Rupak Roy

15.  Example
Let’s say our hypothesis is after
having special classes, is there any
Impact on the scores of the students
with a 95% confidence level
i.e. 0.05 significance level.
In excel:
go to the data tab
then select data analysis
Rupak Roy

16.  Select the ranges
Variable 1: pre scores
Variable 2: post scores
Mean difference: 0
Alpha: 0.05 (95%confidence
level)
in the output we can see the
P-value (one tail) 0.2
which is greater than .05
therefore, we will
conclude that there is no
impact on post scores after
having special classes
and any changes we
see is due to random
chance variation.
Rupak Roy

17. Extra :
One-sample t-test in R-Studio,
kindly refer this in advance analytics courses in R
t.test ( x, alternative=“two-sided”, mu=?, conf.level=?)
Or
t.test( x, alternative=“greater”,mu=?, conf.level=?)
Alternatively,
t.test( x, alternative=“less”, mu=?, conf.level=?)
Here X = Data Range
MU = sample mean/ hypothesis mean difference
(Assume 200 for hypothesis mean difference between two
sample t-test, then we are comparing the mean difference of
two samples is 200 or different. But for this case we have one
sample and let’s say, are the sample is different from the value
200 or not? Hence MU=200)
* conf.level = 0.05 as we remember it’s the confidence level / /
level of significance by default and only required if you want to
change the confidence level.
Rupak Roy

18. Two sample t-test in R studio
 Two Sample Test with equal variances
> t.test (variableRange1,variableRange2, var.equal
=TRUE, alternative=“twosided”, mu=0,paired=FALSE)
Or
>t.test(variableRange1,variableRange2, var.equal
=TRUE, alternative=“greater”, mu=0,paired=FALSE)
Alternatively,
>t.test(variableRange1,variableRange2, var.equal
=TRUE, alternative=“less”, mu=0,paired=FALSE)
 Two Sample Test with unequal variances
> t.test(variableRange1,variableRange2, var.equal
= FALSE, alternative=“twosided”, mu=0,paired=FALSE)
Rupak Roy

19. Paired Sample t- test in R Studio
 For two-sided
> t.test (variableRange1,variableRange2, alternative=
“twosided”, mu= 0, paired= TRUE)
Note: here MU =0 ( the reason is, Ho(null hypothesis), Ha(alternative
hypothesis) we say that means of both the samples different or not
different, that is same as in hypothesis mean difference in excel )
For one-sided ( since R don’t have syntax “ onesided” here we use
syntax “greater” or “less”)
>t.test (variableRange1,variableRange2, alternative= “greater”,
paired= TRUE, conf.level =0.05)
Note: conf.level i.e. confidence level is optional, by default is 0.05
For more details use command
> ?t-test
Rupak Roy

20. Recap
 One tail test and two tail test
 If your Alternative Hypothesis, has an equal sign
in it, this will be a two-tailed test. If it has > or < it
is a one tail test.
 Two sample t-test is used to determine if two
population means/average are equal.
 Paired sample t-test: Calculates the difference
within each before and after pair.
Rupak Roy

21. Next
 In real life we maybe have to compare
means of more than 2 samples.
For this we will use Anova, Chi –square.
Rupak Roy

22. To be continued.
Rupak Roy