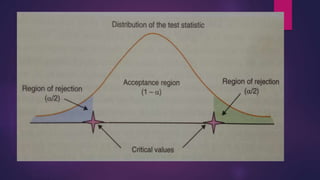
This document discusses the Z-test, a statistical test used to compare means and proportions. The Z-test can be used to test if a sample mean differs from a population mean, if two sample means are equal, or if two population proportions are equal. It assumes the population is normally distributed. The steps involve formulating hypotheses, choosing a significance level, calculating the Z-statistic, and comparing it to a critical value to determine if the null hypothesis should be rejected or accepted. The Z-test is useful when sample sizes are large but requires knowing the population standard deviation.

1. Z - Test
FEMY MONI
ASSISTANT PROFESSOR
ST. ALOYSIUS COLLEGEELTHURUTH

2. INTRODUCTION
 Statistical test of hypothesis is the test conducted to accept or reject the hypothesis.
Commonly used statistical tests are Z-test, t-test, chi-square test, F-test.
 The decision to accept or reject the null hypothesis is made on the basis of a statistic
computed from the sample. Such statistic is known as test statistic (Z, t, F, chi-square).
 Parametric tests are those that make assumptions about the parameters of the population
distribution from which the sample is drawn. This is often the assumption that the
population data are normally distributed.
 Non-parametric tests are “distribution-free” and, as such, can be used for non-Normal
variables.

3. Z- TEST
 Z - test is a statistical tool used for the comparison or determination of the significance of
several statistical measures, particularly the mean in a sample from a normally distributed
population or between two independent samples.
 Z - tests are also based on normal probability distribution.
 Z - test is the most commonly used statistical tool in research methodology.
 Z - test is a Parametric test.

4. USES OF Z-TEST
1. To test the given population mean when the sample is large (30 or more) or when the population
SD is known.
2. To test the equality of two sample means when the samples are large (30 or more) or when the
population SD is known.
3. To test the population proportion.
4. To test the equality of two sample proportions.
5. To test the population SD when the sample is large.
6. To test the equality of two sample standard deviations when the samples are large or when
population standard deviations are known.
7. To test the equality of correlation coefficients.

5. ASSUMPTIONS
1. Sampling distribution of test statistic is normal.
2. Sample statistics are close to the population parameter and therefore for finding standard
error, sample statistics are used in places where population parameters are to be used.

6. STEPS IN CALCULATION
Step 1 : Formulate the hypothesis
Ho : which is stated for the purpose of possible
acceptance. It is the original hypothesis.
H1 : hypothesis other than null hypothesis is called
alternative hypothesis.

7. Step 2: Deciding the level of significance
The level of significance is the probability of rejecting the null hypothesis when it is true,
also known as alpha or ' α '. The commonly used level of significance is either 0.05 or
0.01.
Critical Region
The critical region is called the region of rejection.It is the region in which the null
hypothesis is rejected. The are of critical region is equal to the level of significance, α.

9. Step 3: Calculation of the value
I. Testing The Given Population Mean
Ho: There is no significant difference between sample mean and population mean.
Formula:

10. II. Testing Equality Of Two Population Means.
Ho: There is no significant difference between two means.
Formula:

11. III. Testing Population Proportion
H0: There is no significant difference between sample proportion and population
proportion.
Formula:

12. IV. Testing Equality Of Two Proportions
Ho: There is no significant difference between two population proportions.
Formula:

13. V. Significance Of Difference Between
Sample SD And Population SD
Ho: There is no significant difference between sample SD and population SD.
Formula:

14. VI. Significance Of Difference Between
Standard Deviations Of Two Populations
Ho: There is no significant difference between two standard deviations.
Formula:

15. Step 4: Obtaining the table value and making the decision
The table value is obtained from the 'Table values of z for z - test' by locating the level of
significance and degree of freedom.
For z - test, the degree of freedom is infinity
The decision to accept or reject the null hypothesis is made when;
Calculated value < Table value = Accept Ho
Calculated value > Table value = Reject Ho

16. ADVANTAGES
1. It is a straightforward and reliable test.
2. A Z-score can be used for a comparison of raw scores obtained from different tests.
3. While comparing a set of raw scores, the Z-score considers both the average value and
the variability of those scores.

17. DISADVANTAGES
1. Z-test requires a known standard deviation which is not always possible.
2. It cannot be conducted with a smaller sample size (less than 30).