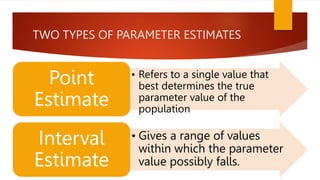
This document discusses basic concepts in estimation, including defining estimation as using a sample to calculate unknown population parameters. It distinguishes between point estimates, which are single values approximating a parameter, and interval estimates, which provide a range of values within which the parameter falls. The document also outlines properties of good estimators such as being unbiased, consistent, and efficient in order to accurately predict population values from samples.