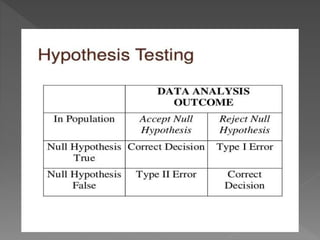
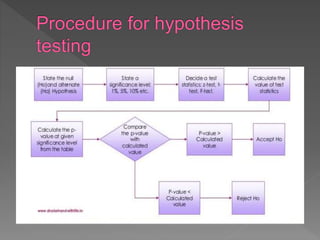
The document discusses hypotheses in research. A hypothesis is a testable statement about the relationship between two variables. Researchers propose a null hypothesis, which states there is no relationship between the variables, and an alternative or experimental hypothesis, which predicts a relationship. Statistical tests are used to analyze data and determine whether to reject the null hypothesis in favor of the alternative hypothesis. The document provides examples of different types of hypotheses and statistical tests used, including t-tests and z-tests.

2.  A hypothesis (plural hypotheses) is a
precise, testable statement of what the
researchers predict will be the outcome of
the study.
 This usually involves proposing a possible
relationship between two variables: the
independent variable (what the researcher
changes) and the dependant variable (what
the research measures).

3.  In research, there is a convention that the
hypothesis is written in two forms, the null
hypothesis, and the alternative hypothesis
(called the experimental hypothesis when
the method of investigation is an
experiment ).
 Briefly, the hypotheses can be expressed in
the following ways:

4.  The null hypothesis states that there is no
relationship between the two variables being
studied (one variable does not affect the
other). It states results are due to chance
and are not significant in terms of supporting
the idea being investigated.

5.  The alternative hypothesis states that
there is a relationship between the two
variables being studied (one variable has an
effect on the other). It states that the results
are not due to chance and that they are
significant in terms of supporting the theory
being investigated.

6.  In order to write the experimental and null
hypotheses for an investigation, you need to
identify the key variables in the study. A variable
is anything that can change or be changed, i.e.
anything which can vary. Examples of variables
are intelligence, gender, memory, ability, time
etc.
 A good hypothesis is short and clear should
include the operationalized variables being
investigated.

7.  Let’s consider a hypothesis that many
teachers might subscribe to: that students
work better on Monday morning than they do
on a Friday afternoon (IV=Day, DV=Standard
of work).

8.  Now, if we decide to study this by giving the
same group of students a lesson on a
Monday morning and on a Friday afternoon
and then measuring their immediate recall
on the material covered in each session we
would end up with the following:

9.  The experimental hypothesis states that
students will recall significantly more
information on a Monday morning than on a
Friday afternoon.
 The null hypothesis states that these will
be no significant difference in the amount
recalled on a Monday morning compared to
a Friday afternoon. Any difference will be
due to chance or confounding factors.

10.  The null hypothesis is, therefore, the
opposite of the experimental hypothesis in
that it states that there will be no change in
behavior.
 At this point you might be asking why we
seem so interested in the null hypothesis.
Surely the alternative (or experimental)
hypothesis is more important?

11.  Well, yes it is. However, we can never 100%
prove the alternative hypothesis. What we do
instead is see if we can disprove, or reject,
the null hypothesis.
 If we can’t reject the null hypothesis, this
doesn’t really mean that our alternative
hypothesis is correct – but it does provide
support for the alternative / experimental
hypothesis.

15.  A one-tailed directional hypothesis predicts
the nature of the effect of the independent
variable on the dependent variable.
 • E.g.: Adults will correctly recall more words
than children.

16.  A two-tailed non-directional hypothesis
predicts that the independent variable will
have an effect on the dependent variable,
but the direction of the effect is not specified.
 • E.g.: There will be a difference in how
many numbers are correctly recalled by
children and adults.

20.  Statistical test to determine whether two
population means are different when the
variance are known and sample size is large.
 Z-Test is a hypothesis test in which the Z-
statistic follow a normal distribution.
 Z-score or Z-statistics is a number
representing the result from the z-test.

21.  A t-test is a type of inferential statistic used to
determine if there is a significant difference
between the means of two groups, which may
be related in certain features.
 follows a normal distribution and may have
unknown variances.
 Calculating a t-test requires three key data
values. They include the difference between the
mean values from each data set (called the
mean difference), the standard deviation of
each group, and the number of data values of
each group

22.  There are three types of t-tests we can
perform based on the data at hand:
 One sample t-test.
 Independent two-sample t-test.
 Paired sample t-test.

23.  In a one-sample t-test, we compare the average (or
mean) of one group against the set average (or
mean). This set average can be any theoretical
value (or it can be the population mean).
 Consider the following example – A research
scholar wants to determine if the average eating
time for a (standard size) burger differs from a set
value. Let’s say this value is 10 minutes. How do
you think the research scholar can go about
determining this?
 He/she can broadly follow the below steps:

24. • Select a group of people
• Record the individual eating time of a standard size burger
• Calculate the average eating time for the group
• Finally, compare that average value with the set value of 10
• That, in a nutshell, is how we can perform a one-sample t-test.
Here’s the formula to calculate this:
where,
•t = t-statistic
•m = mean of the group
•µ = theoretical value or population mean
•s = standard deviation of the group
•n = group size or sample size

25.  The two-sample t-test is used to compare the means of
two different samples.
 Let’s say we want to compare the average height of the
male employees to the average height of the females.
Of course, the number of males and females should be
equal for this comparison. This is where a two-sample t-
test is used.
 Here’s the formula to calculate the t-statistic for a two-
sample t-test:
•mA and mB are the means of two different samples
•nA and nB are the sample sizes

26. Here, the degree of freedom is nA + nB – 2.
We will follow the same logic we saw in a one-sample t-test to check if the
average of one group is significantly different from another group. That’s right –
we will compare the calculated t-statistic with the t-critical value.
•S2 is an estimator of the common variance of two samples, such as:

27.  measure one group at two different times. We compare separate
means for a group at two different times or under two different
conditions.
 For example, a certain manager realized that the productivity
level of his employees was trending significantly downwards. This
manager decided to conduct a training program for all his
employees with the aim of increasing their productivity levels.
 How will the manager measure if the productivity levels
increased? It’s simple – just compare the productivity level of the
employees before versus after the training program.
 Here, we are comparing the same sample (the employees) at two
different times (before and after the training). This is an example
of a paired t-test.

28.  The formula to calculate the t-statistic for a
paired t-test is:
•t = t-statistic
•m = mean of the group
•µ = theoretical value or population mean
•s = standard deviation of the group
•n = group size or sample size