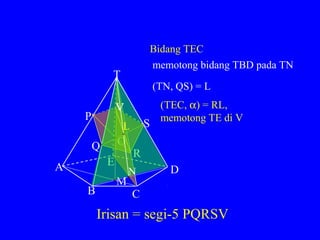
Dokumen ini membahas tentang irisan antara bidang datar dan bangun ruang, termasuk definisi dan sifat-sifat utama dalam menggambar irisan tersebut. Terdapat berbagai teknik untuk menggambar irisan, termasuk menggunakan sumbu afinitas, bidang diagonal, dan perluasan bidang. Contoh diberikan melalui irisan pada kubus dan limas dengan ilustrasi dan penjelasan langkah-langkahnya.

1. T
A
B C
D
E
P
Q
S
R
V
M
O
N
LLL
VV
β
α
T
•
T
•

2. Dimensi tiga:
IRISAN
Oleh: Al. Krismanto, M.Sc.
Widyaiswara
PPPG Matematika Yogyakarta
KELAS III SMU CAWU 1KELAS III SMU CAWU 1

3. PENGERTIAN DASAR
Irisan antarasebuah bidang datar α dengan
sebuah bangun ruang ialah bangun datar yang
semuasisinyaadalah ruasgarispersekutuan
antarabidang α dan bidang sisi bangun ruang
tersebut
Jika bangun ruangnya adalah bidang
banyak maka irisannya adalah sebuah segi
banyak (poligon: segi-n, n ∈ A dan n ≥ 3)

4. DASAR UTAMA MELUKIS IRISAN:
PERSEKUTUAN ANTARA TIGA BIDANG
YANG SALING BERPOTONGAN
KECUALI
TIGA BIDANG
BERSEKUTU
PADA SEBUAH
GARIS

5. JIKA BIDANGNYAJIKA BIDANGNYA αα,, ββ, DAN, DAN γγ
HUBUNGAN-HUBUNGAN YANGHUBUNGAN-HUBUNGAN YANG
DIMAKSUD ADALAHDIMAKSUD ADALAH::
1. Jika α // β
maka (α, γ)//(β, γ)γ tidak sejajar α
γ tidak sejajar β,
α
β
γ
(α, γ)
(β, γ)
(α, γ)
(β, γ)
(α, γ)
(β, γ)
(α, γ)
(β, γ)

6. JIKA BIDANGNYA α, β, DAN γ
HUBUNGAN-HUBUNGAN YANG
DIMAKSUD ADALAH:
2. Jika (α, β) // (α, γ),
maka
(β, γ) // (α, β) // (α, γ)
(α, β)
(α, γ)
α
γ
β (β, γ)

7. JIKA BIDANGNYA α, β, DAN γ
HUBUNGAN-HUBUNGAN YANG
DIMAKSUD ADALAH:
3. Jika (α, β) dan (α, γ)
melalui titik T
maka
(β, γ) juga
melalui titik T
β (β, γ)
(α, β)
γ
(α, γ)α
T•T•T•

8. Contoh
A B
C
D
E F
G
H
•
P
•Q
• R
Diketahui:
Kubus ABCD.EFGH
Titik P pada AE,
Lukislah irisan bidang
PQR terhadap kubus
Q pada DH.
R pada CG

9. 1. MENGGUNAKAN SIFAT DASAR1. MENGGUNAKAN SIFAT DASAR
A B
C
D
E F
G
H
•
P
•Q
• R
ADHE // BCGF
dipotong bidang PQR
karena (ADHE, PQR) = PQ
R pada BCGF dan PQR
Jadi (BCGF, PQR) melalui
R sejajar PQ
Garis tersebut memotong
BF di S
Irisannya adalah segi-4 PQRS
maka (BCGF, PQR) // PQ
⇒(BCGF,PQR)//(ADHE,PQR)
RRRRRRRR
• S• S

10. 2. MENGGUNAKAN BIDANG DIAGONAL
A B
C
D
E F
G
H
P pada AE, R pada CG
Irisan bidang PQR terhadap kubus adalah segi-4 PQRS
•
P
• R
•
M
•Q
Lukis bidang BDHF
(ACGE, BDHF) = MN
Lukis bidang ACGE
•
N
(PR, MN) = titik O
o•
o•
o•
o•
Garis potong ketiga,
(PQR, BDHF) melalui O
→ Tarik QO, memotong
BF di S
•s•
Tarik PR
•s
A B
C
D
E F
G
H
•
P
•Q
• R

11. 3. MENGGUNAKAN SUMBU AFINITAS
B
C
G
H
• K• K
• S
•P
•Q
• R
A
E F
D
• S• S
PERHATIKAN GARIS-GARIS POTONG:
(ADHE, ABCD) = AD
(ADHE, PQR) = QP
(AD, QP) = K
• K • L
(ADHE, ABCD) = AD
(ADHE, PQR) = QP
(AD, QP) = K(PQR, ACGE) = PR
(ABCD, ACGE) = CA
(PR, CA) = M
•
M
sumbu afinitassumbu afinitassumbu afinitassumbu afinitas BC memotong sumbu
afinitas di titik L
Irisannya adalah segi-4 PQRS

13. TIGA TEKNIK LUKISAN IRISAN
1. MENGGUNAKAN SUMBU AFINITAS
2. MENGGUNAKAN BIDANG DIAGONAL
3. MENGGUNAKAN PERLUASAN BIDANG
(SISI)
(CONTOH PADA LIMAS)

14. MENGGUNAKAN SUMBU AFINITAS
K
Lsumbu
afinitas
T
A
B C
D
E
P
Q
R
Diketahui: limas T.ABCDE
P pada TA, Q pada TB,
dan R pada TC
Lukislah: Irisan bidang PQR
terhadap limas
Jawab: Bidang PQR = bidang α
(TAB, alas) = AB
(TAB, α ) = PQ
maka (AB, PQ) = K
(TAC, alas) = AC
(TAC, α ) = PR
maka (AC, PR) = L
Jadi KL adalah sumbu afinitas
KK
LL

15. T
A
B C
D
E
P
Q
S
K
L
M
R
N
V
(TCD, alas) = DC
(alas, α ) = sumbu afinitas KL
(DC, KL) = M
maka (TAC, α ) = MR
Jadi irisannya adalah segi-5 PQRSV
perpanjang DC
sumbu
afinitas
sumbu
afinitas
MR memotong TD di S
SS
MM
(TEC, alas) = EC
memotong sumbu afinitas di N
(TEC, α) = NR
perpanjang EC,
NN
NR memotong TE di V
Tarik PV dan VS

16. MENGGUNAKAN BIDANG DIAGONAL
T
A
B C
D
E
P
Q
S
R
Misal bidang pengiris = bidang PQR
= bidang α )
Lukis bidang TAC (memuat PR
yang juga terletak pada bidang α )
Lukis bidang TBD (memuat Q pada
bidang α )
(AC, BD) = M, maka:
(TAC, TBD) = TM
MMM
(TM, PR) titik O
O
(TBD, α) = QO,
memotong TD di S
OO
SS

17. T
A
B C
D
E
P
Q
S
R
V
Bidang TEC
memotong bidang TBD pada TN
M
O
(TEC, α) = RL,
memotong TE di V
N
(TN, QS) = L
LLL
VV
Irisan = segi-5 PQRSV

18. MENGGUNAKAN PERLUASAN BIDANG
T
A
B C
D
E
P
Q
S
K L
M
R
N
V
MENGGUNAKAN PERLUASAN BIDANG
Perluas bidang-bidang
TBC, TAE, dan TED
(TBC, TAE) = TK
(TBC, TDE) = TL
QR pada TBC memo-
tong TK di M dan TL di N
MM
NNN
Tarik MP, memotong TE di V
VV
Tarik VN, memotong TD di S
SS
Irisan = segi-5 PQRSV