Downloaded 36 times
Uploaded byNgadiyono Ngadiyono
Dimensi tiga
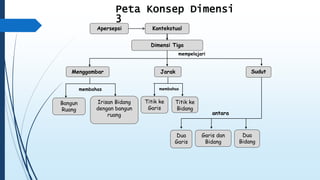
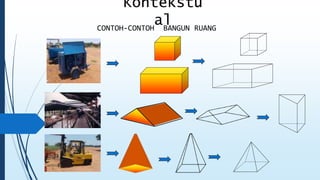
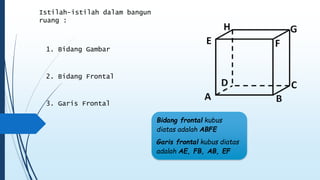
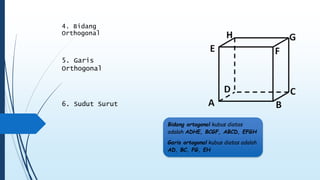
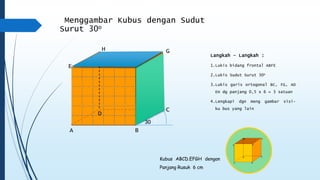
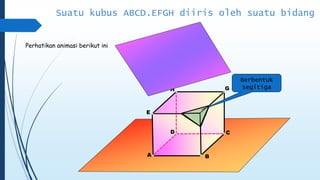
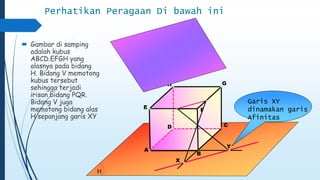
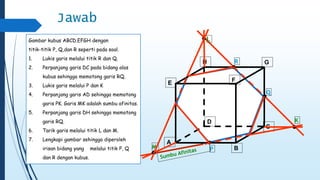
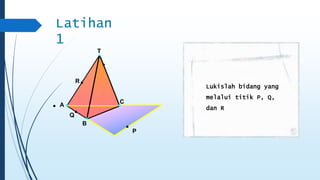
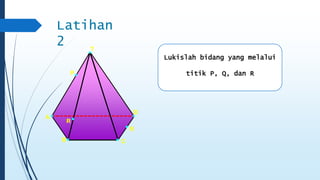
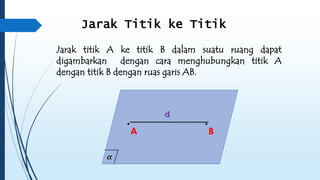
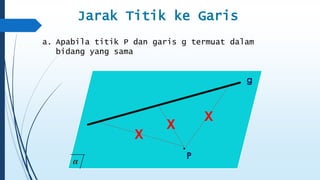
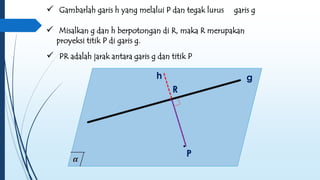
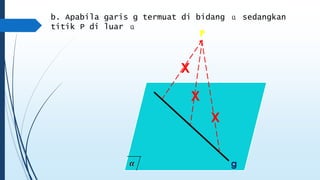
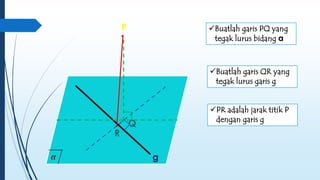
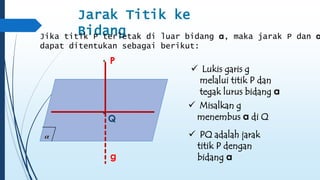
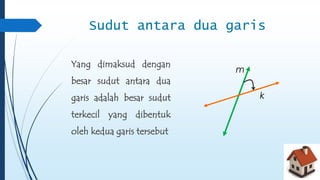
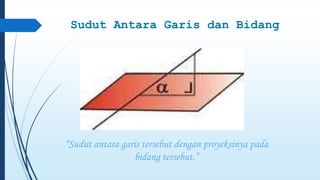
Dokumen ini membahas tentang dimensi tiga, termasuk konsep jarak dan sudut antar garis, bidang, serta pemecahan masalah terkait bangun ruang dimensi tiga. Terdapat juga panduan menggambar bangun ruang dan irisan bidang dengan bangun ruang, serta contoh soal untuk latihan. Selain itu, dokumen ini menjelaskan kompetensi inti dan dasar yang terkait dengan pembelajaran matematika dalam konteks dimensi tiga.
More Related Content
Dimensi tiga
- 1. DIMENSI TIGA Createdby : Annisa Laras (1203075) Ngadiyono (1204829) Sefiana (1204947)
- 2. Peta Konsep Dimensi 3 Dua Bidang Dimensi Tiga mempelajari Garis dan Bidang Titik ke Garis Titik ke Bidang Irisan Bidang dengan bangun ruang Bangun Ruang Kontekstual Menggambar Jarak Sudut membahas membahas antara Dua Garis Apersepsi
- 3. Kompetensi Inti KI1 :Menghayati dan mengamalkan ajaran agama yang dianutnya. KI 2 :Menghayati dan mengamalkan perilaku jujur, disiplin, tanggungjawab, peduli (gotong royong, kerjasama, toleran, damai), santun, responsif dan pro-aktif dan menunjukkan sikap sebagai bagian dari solusi atas berbagai permasalahan dalam berinteraksi secara efektif dengan lingkungan sosial dan alam serta dalam menempatkan diri sebagai cerminan bangsa dalam pergaulan dunia. KI 3 :Memahami, menerapkan, menganalisis pengetahuan faktual, konseptual, prosedural berdasarkan rasa ingintahunya tentang ilmu pengetahuan, teknologi, seni, budaya, dan humaniora dengan wawasan kemanusiaan, kebangsaan, kenegaraan, dan peradaban terkait penyebab fenomena dan kejadian, serta menerapkan pengetahuan prosedural pada bidang kajian yang spesifik sesuai dengan bakat dan minatnya untuk memecahkan masalah. KI 4 :Mengolah, menalar, dan menyaji dalam ranah konkret dan ranah abstrak terkait dengan pengembangan dari yang dipelajarinya di sekolah secara mandiri, dan mampu menggunakan metoda sesuai kaidah keilmuan
- 4. Kompetensi Dasar 3.5Memahami konsep jarak dan sudut antar garis/bidang, bidang/bidang dan irisan dua bidang dalam bangun ruang dimensi tiga melalui demonstrasi menggunakan alat peraga atau media lainnya 4.4 Menggunakan konsep jarak, sudut antar garis/bidang, bidang/bidang, dan irisan dua bidang dalam pemecahan masalah bangun ruang dimensi tiga
- 5. Apreseps i Pernahkahkalian melihat film tiga dimensi dimensi (3D)? Jadi apa itu dimensi tiga? Lalu bisakah kalian menyebutkan bangun-bangun dimensi tiga?
- 6. Kontekstu al CONTOH-CONTOHBANGUN RUANG
- 8. DIMENSI TIGA Menggambarbangun ruang Irisan Bidang dengan bangun ruang Menentukan jarak pada bangun ruang Sudut pada bangun ruang
- 9.
- 10. Istilah-istilah dalam bangun ruang : 2. Bidang Frontal 3. Garis Frontal Bidang frontal kubus diatas adalah ABFE Garis frontal kubus diatas adalah AE, FB, AB, EF 1. Bidang Gambar
- 11. 4. Bidang Orthogonal 5. Garis Orthogonal Bidang ortogonal kubus diatas adalah ADHE, BCGF, ABCD, EFGH Garis ortogonal kubus diatas adalah AD, BC, FG, EH 6. Sudut Surut
- 12. Langkah-Langkah Menggambar Bangun Ruang : 1. Lukis bidang frontal yang diinginkan dgn ukuran sebenarnya 2. Lukis sudut surut 3. Lukis bidang ortogonal bawah sesuai dg sudut surut dan perbandingan proyeksi yg diminta 4. Lengkapi lukisan bidang-bidang yg ada sesuai dasar langkah 1, 2 dan 3 (Ari Damari : 2005)
- 13. Menggambar Kubus denganSudut Surut 30o Lukisan Kubus Dgn Bidangn Frontal ABFE Kubus ABCD.EFGH dengan Panjang Rusuk 6 cm E F A B 30 Langkah – Langkah : 1.Lukis bidang frontal ABFE 2.Lukis Sudut Surut 30o 3.Lukis garis ortogonal BC, FG, AD EH dg panjang 0,5 x 6 = 3 satuan 4.Lengkapi dgn meng gambar sisi-ku bus yang lain G C H D
- 14. LATIHA N GambarlahKubus dengan Sudut Surut 120 o!
- 15. IRISAN BIDANG DENGAN BANGUN RUANG
- 16. Suatu kubus ABCD.EFGHdiiris oleh suatu bidang H E A G D B C F Berbentuk segitiga Perhatikan animasi berikut ini
- 17. Perhatikan Peragaan Dibawah ini H E A G F D B C H Garis XY dinamakan garis Afinitas X Y Gambar di samping adalah kubus ABCD.EFGH yang alasnya pada bidang H. Bidang V memotong kubus tersebut sehingga terjadi irisan bidang PQR. Bidang V juga memotong bidang alas H sepanjang garis XY
- 18. 18 Sumbu afinitasadalah garis potong antara bidang irisan dengan alas bangun ruang yang diirisnya. Aksioma yang diperlukan dalam melukis bidang irisan: 1. Dua titik menentukan garis. 2. Garis dapat diperpanjang pada kedua ujungnya. 3. Bidang dapat diperluas.
- 19. 1. Pilih duatitik pada bidang irisan yang terletak sebidang pada bangun ruang. 2. Lukislah garis yang melalui dua titik tersebut. 3. Perpanjang garis-garis pada alas bangun ruang sehingga memotong garis pada langkah 2. 4. Hubungkan 2 titik baru pada bidang alas bangun ruang. Garis yang diperoleh adalah sumbu afinitas. 5. Lengkapi gambar irisan bidang tersebut.
- 20. Contoh 1 Diketahuikubus ABCD.EFGH dengan titik-titik P, Q, dan R berturut–turut terletak pada pertengahan AB, CG, dan GH. Lukislah bidang irisan kubus ABCD.EFGH yang melalui titik P, Q, dan R!
- 21. C B A D E H G F Q R P K L M Jawab Gambar kubus ABCD.EFGH dengan titik-titik P, Q,dan R seperti pada soal. 1. Lukis garis melalui titik R dan Q. 2. Perpanjang garis DC pada bidang alas kubus sehingga memotong garis RQ. 3. Lukis garis melalui P dan K 4. Perpanjang garis AD sehingga memotong garis PK. Garis MK adalah sumbu afinitas. 5. Perpanjang garis DH sehingga memotong garis RQ. 6. Tarik garis melalui titik L dan M. 7. Lengkapi gambar sehingga diperoleh irisan bidang yang melalui titik P, Q dan R dengan kubus.
- 22. T R A B C Q P Latihan 1 Lukislah bidang yang melalui titik P, Q, dan R
- 23. Lukislah bidang yangmelalui titik P, Q, dan R T A B C D P R R Latihan 2
- 24. Lukislah bidang yangmelalui titik H, P, dan K Latihan 3 H I F E J A B C D G L K P
- 25. MENENTUKAN JARAK PADA BANGUN RUANG
- 26. Materi Ajar 1.Jarak titik ke titik 2. Jarak titik ke garis 3. Jarak titik ke bidang
- 27. Jarak Titik keTitik Jarak titik A ke titik B dalam suatu ruang dapat digambarkan dengan cara menghubungkan titik A dengan titik B dengan ruas garis AB. . A . B d
- 28. LATIHAN Diketahui kubusABCD.EFGH dengan panjang rusuk 5 cm. Titik P pertengahan rusuk CG. Hitunglah jarak titik A ke D Hitunglah jarak titik A ke C Hitunglah jarak titik C ke E Hitunglah jarak titik A ke P
- 29. Jarak Titik keGaris a. Apabila titik P dan garis g termuat dalam bidang yang sama . P g X X X
- 30. Gambarlah garish yang melalui P dan tegak lurus garis g Misalkan g dan h berpotongan di R, maka R merupakan PR adalah jarak antara garis g dan titik P h g . P proyeksi titik P di garis g. .R
- 31. b. Apabila garisg termuat di bidang α sedangkan titik P di luar α .P g X X X
- 32. .P PR adalahjarak titik P dengan garis g .R g Buatlah garis PQ yang tegak lurus bidang α Buatlah garis QR yang tegak lurus garis g . Q
- 33. Latiha n Diketahuikubus ABCD.EFGH dengan panjang rusuk 5 cm. Hitung jarak titik D ke garis BC dan jarak dari titik B ke garis EG
- 34. Jarak Titik ke Bidang Jika titik P terletak di luar bidang α, maka jarak P dan α dapat ditentukan sebagai berikut: . P Lukis garis g melalui titik P dan tegak lurus bidang α Misalkan g menembus α di Q . Q g PQ adalah jarak titik P dengan bidang α
- 35. Latihan 1 Diketahuilimas tegak T.ABCD dengan bidang alas ABCD berbentuk persegi panjang dengan AB = 4 cm, BC = 3 cm dan TA = TB = TC =TD = 6,5 cm. Hitunglah : a. Panjang AC b. Jarak titik puncak T ke bidang alas ABCD
- 36. Latihan 2 휟푨푩푪adalah segitiga sama kaki pada bidang horizontal dan BCDE persegi panjang pada bidang vertikal dengan AC = AB, AD = 17 cm, CD = 8 cm dan ED = 18 cm hitunglah: a. Panjang AC b. Jarak titik A ke bidang BCDE
- 37. SUDUT PADA BANGUNRUANG
- 38. Materi Ajar 1.Sudut antara dua garis 2. Sudut antara garis dan bidang 3. Sudut antara dua bidang
- 39. Sudut antara duagaris Yang dimaksud dengan besar sudut antara dua garis adalah besar sudut terkecil yang dibentuk oleh kedua garis tersebut k m
- 40. Sudut Antara Garisdan Bidang “Sudut antara garis tersebut dengan proyeksinya pada bidang tersebut.”
- 41. Sudut Antara Garisdan Bidang “Kedudukan garis dengan bidang dimana garis menembus bidang dapat ditentukan sudut antara garis dengan bidang.” Misalnya, garis g menembus bidang V di titik A. Maka untuk menentukan sudut antara garis dengan bidang dapat dilakukan langkah-langkah sebagai berikut : 1. Tetapkan satu titik sembarang pada garis g di luar bidang V, misalkan titik B 2. Proyeksikan titik B pada bidang V, misalkan titik B’ 3. Hubungkan titik A dengan titik B’ 4. Sudut BAB’ merupakan sudut antara garis g dan bidang V V g A B B’ a
- 42. Contoh Soal: Diketahuikubus ABCD.EFGH. Tentukan sudut antara CE dengan bidang ABCD Jawab: Tetapkan satu titik pada garis CE di luar bidang ABCD, yaitu titik E Proyeksikan titik E pada bidang ABCD yaitu titik A Hubungkan titik A dengan titik C Sudut ECA merupakan sudut antara garis CE dengan bidang ABCD A H G C B E F D a
- 43. Sudut Antara DuaBidang Sudut antara dua garis yang terletak pada masing-masing bidang tersebut. Dimana garis-garis ini tegak lurus pada garis potong dua bidang (garis tumpuan) itu; dan berpotongan di garis potong kedua bidang.
- 44. Sudut Antara DuaBidang Sudut antara bidang U dan bidang V (berpotongan) dapat ditentukan dengan cara sebagai berikut : 1. Tetapkan garis persekutuan bidang U dengan bidang V yaitu (U,V) 2. Tetapkan sebuah titik P pada garis (U,V) 3. Pada bidang U, buat garis melalui P tegak lurus garis (U,V) yaitu PQ 4. Pada bidang V, buat garis melalui P tegak lurus garis (U,V) yaitu PR 5. Sudut QPR adalah sudut antara bidang U dan bidang V V U (V,U) R Q P
- 45. Contoh Soal: KubusABCD.EFGH dengan panjang rusuk 6 cm. Titik P di tengah EF dan R di tengah GH. Tentukan sudut antara bidang ADRP dengan bidang BCRP Jawab: Tentukan garis persekutuan bidang ADRP dengan bidang BCRP yaitu RP Tetapkan sebuah titik T pada garis RP (T di tengah RP) Pada bidang BCRP, buat garis melalui T tegak lurus RP yaitu TL Pada bidang ADRP, buat garis melalui T tegak lurus RP yaitu TK Sudut KTL merupakan sudut antara dua bidang A H G C B E F D R P K T L