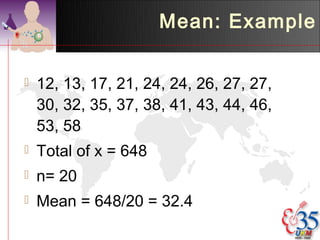
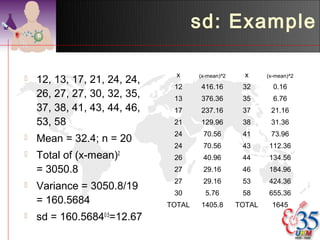
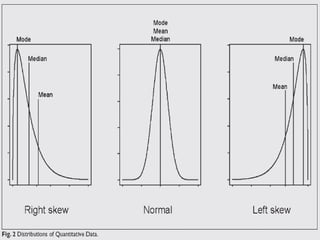
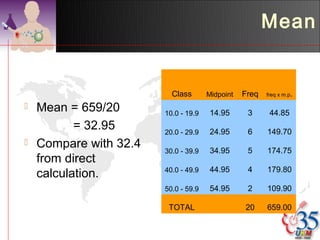
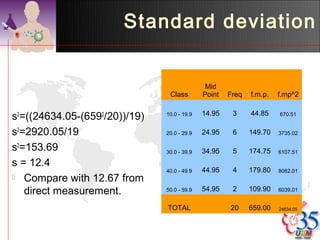
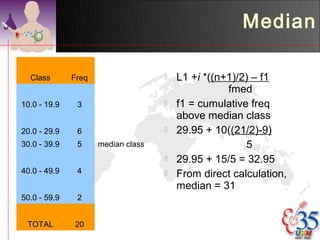
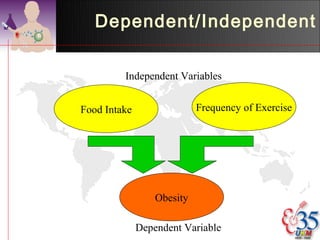
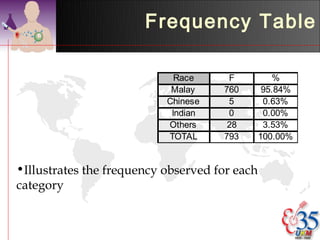
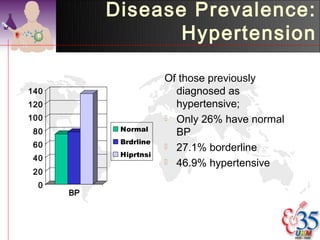
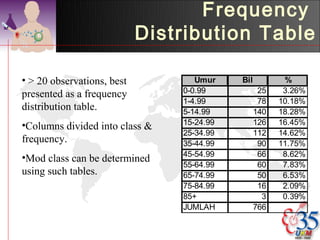
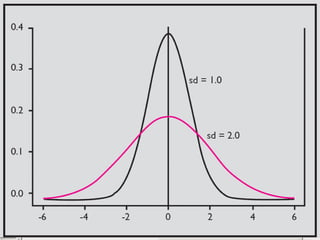
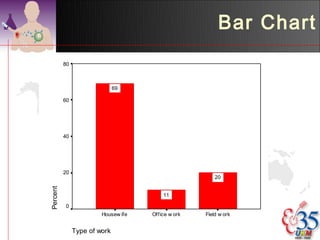
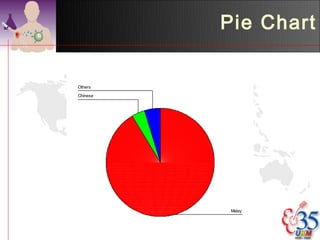
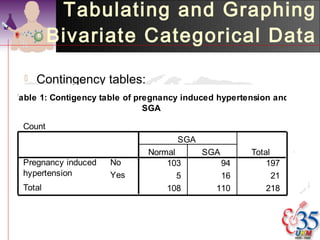
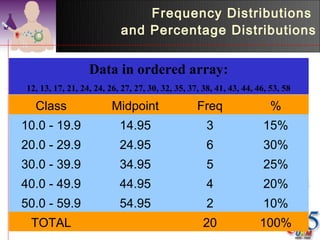
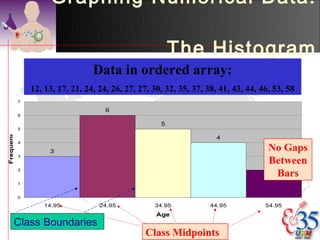
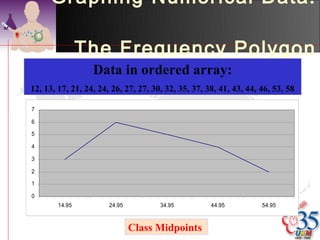
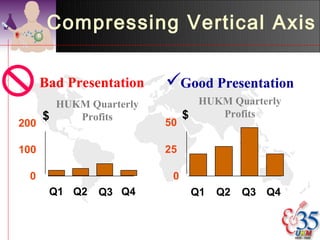
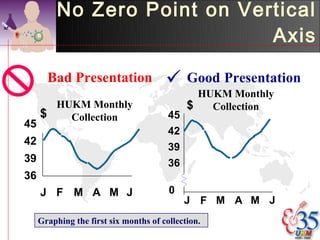
This document describes various methods of descriptive data analysis, including: 1) Descriptive analysis uses measures of central tendency like mean, median, and mode to summarize large datasets. It is used to describe data through tables and diagrams. 2) Variables can be categorized as dependent or independent. Descriptive analysis examines relationships between these types of variables. 3) Common descriptive methods include frequency distributions, measures of central tendency and variability, as well as graphical presentations like histograms, bar charts, and scatter plots. These methods organize and illustrate key characteristics of quantitative data.

1. Medicine & Society II
Descriptive Analysis
Dr Azmi Mohd Tamil
Dept of Community Health
Universiti Kebangsaan Malaysia

2. Introduction
Types of Variables

3. Dependent/Independent
Independent Variables
Food Intake Frequency of Exercise
Obesity
Dependent Variable

5. Data Analysis
 Descriptive
 Bivariate
 Multivariate

6. Descriptive
 Summarise a large set of data by a few
meaningful numbers.
 For the purpose of describing the data
 Example; in one year, what kind of cases are
treated by the Psychiatric Dept?
 Tables & diagrams are usually used to
describe the data
 For numerical data, measures of central
tendency & spread is usually used

7. Frequency Table
Race F %
Malay 760 95.84%
Chinese 5 0.63%
Indian 0 0.00%
Others 28 3.53%
TOTAL 793 100.00%
•Illustrates the frequency observed for each
category

8. Disease Prevalence:
Hypertension
Of those previously
140 diagnosed as
120 hypertensive;
100  Only 26% have normal
80 Normal
BP
60 Brdrline
 27.1% borderline
Hiprtnsi
40  46.9% hypertensive
20
0
BP

9. Frequency
Distribution Table
• > 20 observations, best Umur Bil %
presented as a frequency 0-0.99 25 3.26%
1-4.99 78 10.18%
distribution table. 5-14.99 140 18.28%
•Columns divided into class & 15-24.99 126 16.45%
25-34.99 112 14.62%
frequency. 35-44.99 90 11.75%
45-54.99 66 8.62%
•Mod class can be determined
55-64.99 60 7.83%
using such tables. 65-74.99 50 6.53%
75-84.99 16 2.09%
85+ 3 0.39%
JUMLAH 766

10. Measurement of Central
Tendency & Spread

11. Measures of Central
Tendency
 Mean
 Mode
 Median

12. Variability
 Standard deviation
 Inter-quartiles
 Skewness & kurtosis

13. Mean
 the average of the data collected
 To calculate the mean, add up the
observed values and divide by the
number of them.
 A major disadvantage of the mean is
that it is sensitive to outlying points

14. Mean: Example
 12, 13, 17, 21, 24, 24, 26, 27, 27,
30, 32, 35, 37, 38, 41, 43, 44, 46,
53, 58
 Total of x = 648
 n= 20
 Mean = 648/20 = 32.4

15. Measures of variation -
standard deviation
 tells us how much all the scores in a dataset cluster around the
mean. A large sd is indicative of a more varied data scores.
 a summary measure of the differences of each observation from
the mean.
 If the differences themselves were added up, the positive would
exactly balance the negative and so their sum would be zero.
 Consequently the squares of the differences are added.

16. sd: Example
x (x-mean)^2 x (x-mean)^2
 12, 13, 17, 21, 24, 24,
12 416.16 32 0.16
26, 27, 27, 30, 32, 35, 13 376.36 35 6.76
37, 38, 41, 43, 44, 46, 17 237.16 37 21.16
53, 58 21 129.96 38 31.36
24 70.56 41 73.96
 Mean = 32.4; n = 20
24 70.56 43 112.36
 Total of (x-mean)2 26 40.96 44 134.56
= 3050.8 27 29.16 46 184.96
27 29.16 53 424.36
 Variance = 3050.8/19
30 5.76 58 655.36
= 160.5684 TOTAL 1405.8 TOTAL 1645
 sd = 160.56840.5=12.67

18. Median
 the ranked value that lies in the middle
of the data
 the point which has the property that
half the data are greater than it, and half
the data are less than it.
 if n is even, average the n/2th largest
and the n/2 + 1th largest observations
 "robust" to outliers

19. Median:
 12, 13, 17, 21, 24, 24, 26, 27, 27, 30,
32, 35, 37, 38, 41, 43, 44, 46, 53, 58
 (20+1)/2 = 10th which is 30, 11th is 32
 Therefore median is (30 + 32)/2 = 31

20. Measures of variation -
quartiles
 The range is very susceptible to what
are known as outliers
 A more robust approach is to divide the
distribution of the data into four, and find
the points below which are 25%, 50%
and 75% of the distribution. These are
known as quartiles, and the median is
the second quartile.

21. Quartiles
 12, 13, 17, 21, 24,
24, 26, 27, 27, 30,
32, 35, 37, 38, 41,
43, 44, 46, 53, 58
 25th percentile 24; (24+24)/2
 50th percentile 31; (30+32)/2
 75th percentile 42.5; (41+43)/2

22. Mode
 The most frequent occurring number.
E.g. 3, 13, 13, 20, 22, 25: mode = 13.
 It is usually more informative to quote
the mode accompanied by the
percentage of times it happened; e.g,
the mode is 13 with 33% of the
occurrences.

23. Mode: Example
 12, 13, 17, 21, 24, 24, 26, 27, 27, 30,
32, 35, 37, 38, 41, 43, 44, 46, 53, 58
 Modes are 24 (10%) & 27 (10%)

24. Mean or Median?
 Which measure of central tendency
should we use?
 if the distribution is normal, the mean
will be the measure to be presented,
otherwise the median should be more
appropriate.

26. Presentation
Qualitative & Quantitative Data
Charts & Tables

27. Presentation
Qualitative Data

28. Graphing Categorical Data:
Univariate Data
Categorical Data
Graphing Data
Tabulating Data
The Summary Table
Pie Charts
CD
S avings
B onds Bar Charts Pareto Diagram
S toc k s 45 120
40
100
0 10 20 30 40 50 35
30 80
25
60
20
15 40
10
20
5
0 0
S toc k s B onds S avings CD

29. Bar Chart
80
69
60
40
20
20
Percent
11
0
Housew ife Office w ork Field w ork
Type of work

30. Pie Chart
Others
Chinese
Malay

31. Tabulating and Graphing
Bivariate Categorical Data
 Contingency tables:
Table 1: Contigency table of pregnancy induced hypertension and
SGA
Count
SGA
Normal SGA Total
Pregnancy induced No 103 94 197
hypertension Yes 5 16 21
Total 108 110 218

32. Tabulating and Graphing
Bivariate Categorical Data
120
 Side
by
100 103
94
side 80
charts
60
40
SGA
20
Normal
Count
16
0 SGA
No Yes
Pregnancy induced hypertension

33. Presentation
Quantitative Data

34. Tabulating and Graphing
Numerical Data
Numerical Data 41, 24, 32, 26, 27, 27, 30, 24, 38, 21
Frequency Distributions
Ordered Array Ogive
Cumulative Distributions 120
21, 24, 24, 26, 27, 27, 30, 32, 38, 41 100
80
60
40
20
0
2 144677 Area
Stem and Leaf Histograms
10 20 30 40 50 6
Display 3 028 7
6
4 1 5
Tables Polygons
4
3
2
1
0
10 20 30 40 50 60

35. Tabulating Numerical
Data: Frequency
Distributions
 Sort raw data in ascending order:
12, 13, 17, 21, 24, 24, 26, 27, 27, 30, 32, 35, 37, 38, 41, 43,
44, 46, 53, 58
 Find range: 58 - 12 = 46
 Select number of classes: 5 (usually between 5 and 15)
 Compute class interval (width): 10 (46/5 then round up)
 Determine class limits: 10.0-19.9, 20.0-29.9, 30.0-39.9 etc
 Determine class boundaries: e.g. (19.9+20.0)/2=19.95
 Compute class midpoints: e.g. (10+19.9)/2 = 14.95
 Count observations & assign to classes (i.e. use tally
method)

36. Frequency Distributions
and Percentage Distributions
Data in ordered array:
12, 13, 17, 21, 24, 24, 26, 27, 27, 30, 32, 35, 37, 38, 41, 43, 44, 46, 53, 58
Class Midpoint Freq %
10.0 - 19.9 14.95 3 15%
20.0 - 29.9 24.95 6 30%
30.0 - 39.9 34.95 5 25%
40.0 - 49.9 44.95 4 20%
50.0 - 59.9 54.95 2 10%
TOTAL 20 100%

37. Graphing Numerical Data:
The Histogram
Data in ordered array:
12, 13, 17, 21, 24, 24, 26, 27, 27, 30, 32, 35, 37, 38, 41, 43, 44, 46, 53, 58
7
6
6
5
5
Frequency
4
4
3 No Gaps
Between
3
2
2
Bars
1
0
14.95 24.95 34.95 44.95 54.95
Age
Class Boundaries
Class Midpoints

38. Graphing Numerical Data:
The Frequency Polygon
Data in ordered array:
12, 13, 17, 21, 24, 24, 26, 27, 27, 30, 32, 35, 37, 38, 41, 43, 44, 46, 53, 58
7
6
5
4
3
2
1
0
14.95 24.95 34.95 44.95 54.95
Class Midpoints

39. Calculate Measures of
Central Tendency & Spread
 We can use frequency distribution table
to calculate;
• Mean
• Standard Deviation
• Median
• Mode

40. Mean
Class Midpoint Freq freq x m.p.
 Mean = 659/20 10.0 - 19.9 14.95 3 44.85
= 32.95 20.0 - 29.9 24.95 6 149.70
 Compare with 32.4 30.0 - 39.9 34.95 5 174.75
from direct
40.0 - 49.9 44.95 4 179.80
calculation.
50.0 - 59.9 54.95 2 109.90
TOTAL 20 659.00

41. Standard deviation
Mid
Class Point Freq f.m.p. f.mp^2
14.95 3 44.85
s2=((24634.05-(6592/20))/19) 10.0 - 19.9 670.51
s2=2920.05/19 20.0 - 29.9 24.95 6 149.70 3735.02
s2=153.69 30.0 - 39.9 34.95 5 174.75 6107.51
s = 12.4
40.0 - 49.9 44.95 4 179.80 8082.01
 Compare with 12.67 from
direct measurement. 50.0 - 59.9 54.95 2 109.90 6039.01
TOTAL 20 659.00 24634.05

42. Median
Class Freq  L1 +i *((n+1)/2) – f1
fmed
10.0 - 19.9 3  f1 = cumulative freq
above median class
20.0 - 29.9 6  29.95 + 10((21/2)-9)
30.0 - 39.9 5 median class 5
 29.95 + 15/5 = 32.95
40.0 - 49.9 4  From direct calculation,
median = 31
50.0 - 59.9 2
TOTAL 20

43. Mode
=L1 +i *(Beza1/(Beza1+Beza2))
Class Freq
=19.95 + 10(3/(3+1))
=27.45
10.0 - 19.9 3
20.0 - 29.9 6 mode class
 Compare with
modes of 24 & 27 30.0 - 39.9 5
from direct 40.0 - 49.9 4
calculation.
50.0 - 59.9 2
TOTAL 20

44. Graphing Bivariate Numerical
Data (Scatter Plot )
5.0
4.5
4.0
3.5
3.0
2.5
Birth weight
2.0
1.5 Rsq = 0.2028
30 40 50 60 70 80 90 100
Weight at first ANC

45. Principles of Graphical
Excellence
 Presents data in a way that provides
substance, statistics and design
 Communicates complex ideas with
clarity, precision and efficiency
 Gives the largest number of ideas in the
most efficient manner
 Almost always involves several
dimensions
 Tells the truth about the data

46. Errors in Presenting Data
 Using “chart junk”
 Failing to provide a relative
basis in comparing data
between groups
 Compressing the vertical axis
 Providing no zero point on the vertical
axis

47. “Chart Junk”
Bad Presentation
Minimum charge  Good Presentation
per visit Minimum charge
1960: $1.00 $ per visit
4
1970: $1.60
2
1980: $3.10
0
1990: $3.80 1960 1970 1980 1990

48. No Relative Basis
Bad Presentation  Good Presentation
A’s received by A’s received by
Freq. students. students.
300 30 %
200 20
100 10
0 0
Yr1 Yr2 Yr3 Yr4 Yr1 Yr2 Yr3 Yr4

49. Compressing Vertical Axis
Bad Presentation Good Presentation
HUKM Quarterly HUKM Quarterly
$ Profits $ Profits
200 50
100 25
0 0
Q1 Q2 Q3 Q4 Q1 Q2 Q3 Q4

50. No Zero Point on Vertical
Axis
Bad Presentation  Good Presentation
HUKM Monthly
HUKM Monthly $ Collection
$ Collection 45
45
42
42
39
39 36
36
J F M A M J 0
J F M A M J
Graphing the first six months of collection.